Scaled stochastic gradient descent for low-rank matrix completion
Paper and Code
Oct 05, 2016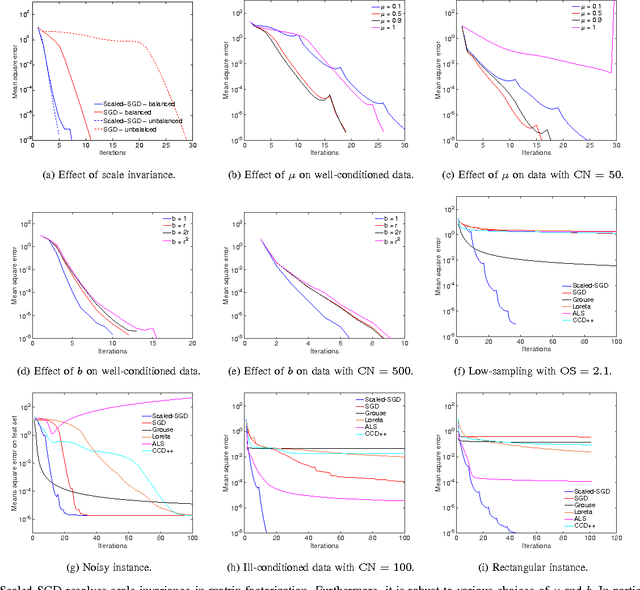


The paper looks at a scaled variant of the stochastic gradient descent algorithm for the matrix completion problem. Specifically, we propose a novel matrix-scaling of the partial derivatives that acts as an efficient preconditioning for the standard stochastic gradient descent algorithm. This proposed matrix-scaling provides a trade-off between local and global second order information. It also resolves the issue of scale invariance that exists in matrix factorization models. The overall computational complexity is linear with the number of known entries, thereby extending to a large-scale setup. Numerical comparisons show that the proposed algorithm competes favorably with state-of-the-art algorithms on various different benchmarks.
* Accepted to IEEE CDC 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge