PETRA: Parallel End-to-end Training with Reversible Architectures

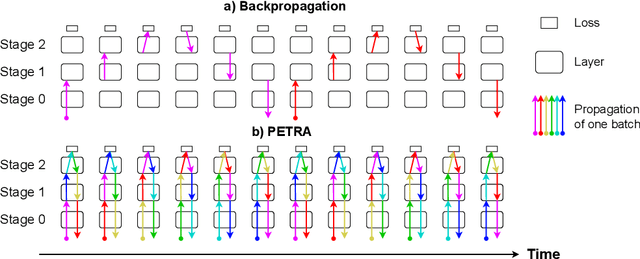
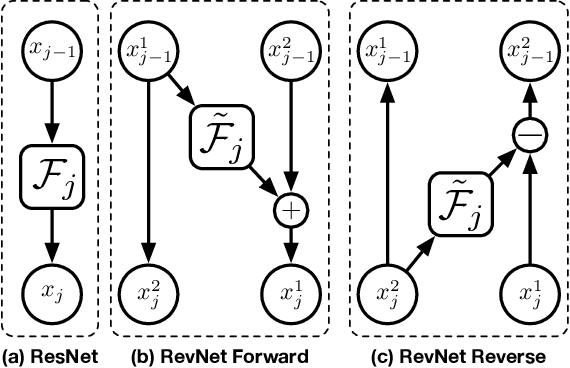
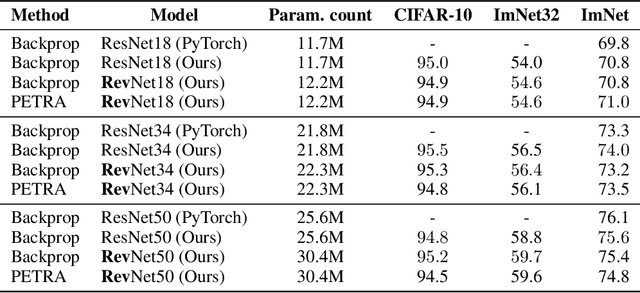
Reversible architectures have been shown to be capable of performing on par with their non-reversible architectures, being applied in deep learning for memory savings and generative modeling. In this work, we show how reversible architectures can solve challenges in parallelizing deep model training. We introduce PETRA, a novel alternative to backpropagation for parallelizing gradient computations. PETRA facilitates effective model parallelism by enabling stages (i.e., a set of layers) to compute independently on different devices, while only needing to communicate activations and gradients between each other. By decoupling the forward and backward passes and keeping a single updated version of the parameters, the need for weight stashing is also removed. We develop a custom autograd-like training framework for PETRA, and we demonstrate its effectiveness on CIFAR-10, ImageNet32, and ImageNet, achieving competitive accuracies comparable to backpropagation using ResNet-18, ResNet-34, and ResNet-50 models.

Smoothed analysis of the low-rank approach for smooth semidefinite programs

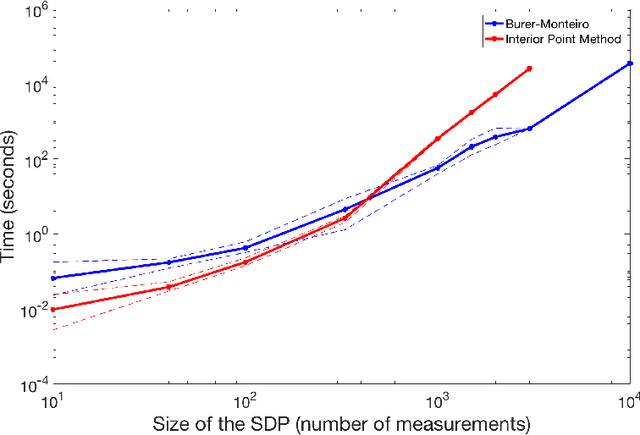
We consider semidefinite programs (SDPs) of size n with equality constraints. In order to overcome scalability issues, Burer and Monteiro proposed a factorized approach based on optimizing over a matrix Y of size $n$ by $k$ such that $X = YY^*$ is the SDP variable. The advantages of such formulation are twofold: the dimension of the optimization variable is reduced and positive semidefiniteness is naturally enforced. However, the problem in Y is non-convex. In prior work, it has been shown that, when the constraints on the factorized variable regularly define a smooth manifold, provided k is large enough, for almost all cost matrices, all second-order stationary points (SOSPs) are optimal. Importantly, in practice, one can only compute points which approximately satisfy necessary optimality conditions, leading to the question: are such points also approximately optimal? To this end, and under similar assumptions, we use smoothed analysis to show that approximate SOSPs for a randomly perturbed objective function are approximate global optima, with k scaling like the square root of the number of constraints (up to log factors). We particularize our results to an SDP relaxation of phase retrieval.