Synchronization on circles and spheres with nonlinear interactions

We consider the dynamics of $n$ points on a sphere in $\mathbb{R}^d$ ($d \geq 2$) which attract each other according to a function $\varphi$ of their inner products. When $\varphi$ is linear ($\varphi(t) = t$), the points converge to a common value (i.e., synchronize) in various connectivity scenarios: this is part of classical work on Kuramoto oscillator networks. When $\varphi$ is exponential ($\varphi(t) = e^{\beta t}$), these dynamics correspond to a limit of how idealized transformers process data, as described by Geshkovski et al. (2024). Accordingly, they ask whether synchronization occurs for exponential $\varphi$. In the context of consensus for multi-agent control, Markdahl et al. (2018) show that for $d \geq 3$ (spheres), if the interaction graph is connected and $\varphi$ is increasing and convex, then the system synchronizes. What is the situation on circles ($d=2$)? First, we show that $\varphi$ being increasing and convex is no longer sufficient. Then we identify a new condition (that the Taylor coefficients of $\varphi'$ are decreasing) under which we do have synchronization on the circle. In so doing, we provide some answers to the open problems posed by Geshkovski et al. (2024).

Perceptual adjustment queries and an inverted measurement paradigm for low-rank metric learning

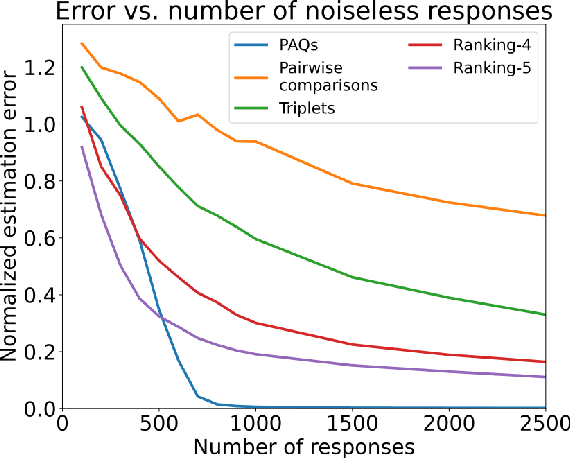
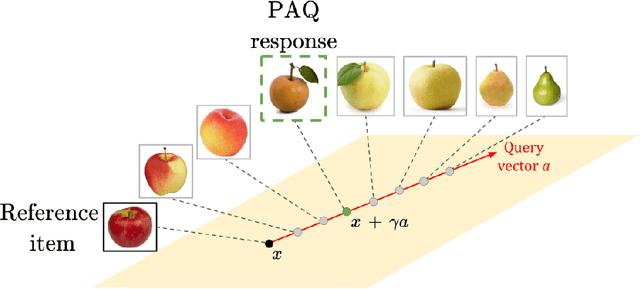
We introduce a new type of query mechanism for collecting human feedback, called the perceptual adjustment query ( PAQ). Being both informative and cognitively lightweight, the PAQ adopts an inverted measurement scheme, and combines advantages from both cardinal and ordinal queries. We showcase the PAQ in the metric learning problem, where we collect PAQ measurements to learn an unknown Mahalanobis distance. This gives rise to a high-dimensional, low-rank matrix estimation problem to which standard matrix estimators cannot be applied. Consequently, we develop a two-stage estimator for metric learning from PAQs, and provide sample complexity guarantees for this estimator. We present numerical simulations demonstrating the performance of the estimator and its notable properties.

New Equivalences Between Interpolation and SVMs: Kernels and Structured Features

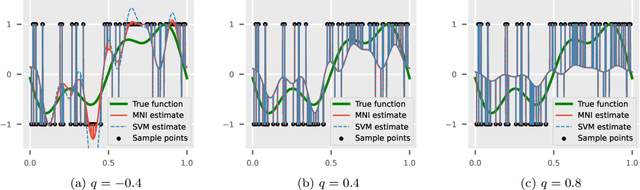
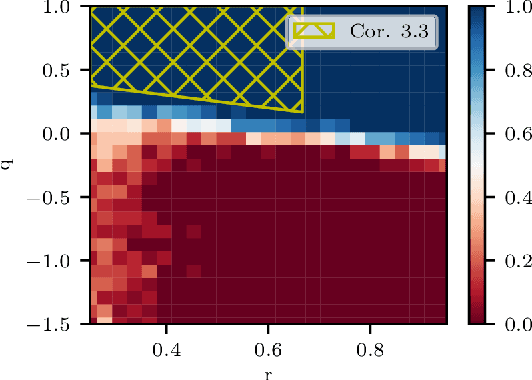
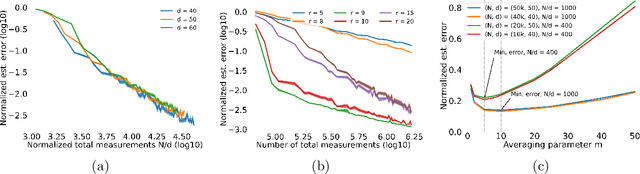
The support vector machine (SVM) is a supervised learning algorithm that finds a maximum-margin linear classifier, often after mapping the data to a high-dimensional feature space via the kernel trick. Recent work has demonstrated that in certain sufficiently overparameterized settings, the SVM decision function coincides exactly with the minimum-norm label interpolant. This phenomenon of support vector proliferation (SVP) is especially interesting because it allows us to understand SVM performance by leveraging recent analyses of harmless interpolation in linear and kernel models. However, previous work on SVP has made restrictive assumptions on the data/feature distribution and spectrum. In this paper, we present a new and flexible analysis framework for proving SVP in an arbitrary reproducing kernel Hilbert space with a flexible class of generative models for the labels. We present conditions for SVP for features in the families of general bounded orthonormal systems (e.g. Fourier features) and independent sub-Gaussian features. In both cases, we show that SVP occurs in many interesting settings not covered by prior work, and we leverage these results to prove novel generalization results for kernel SVM classification.

Harmless interpolation in regression and classification with structured features

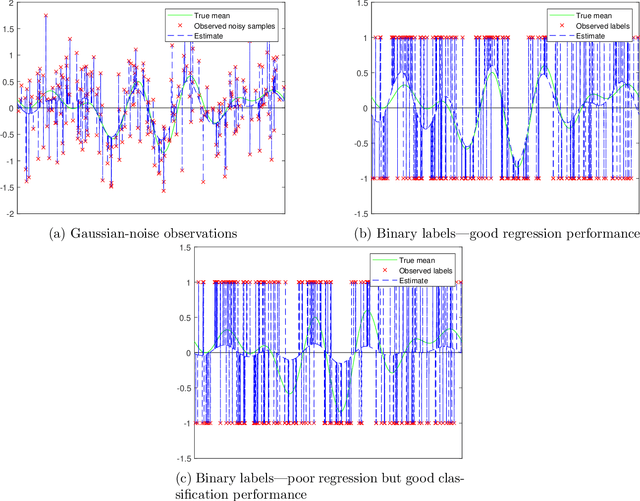
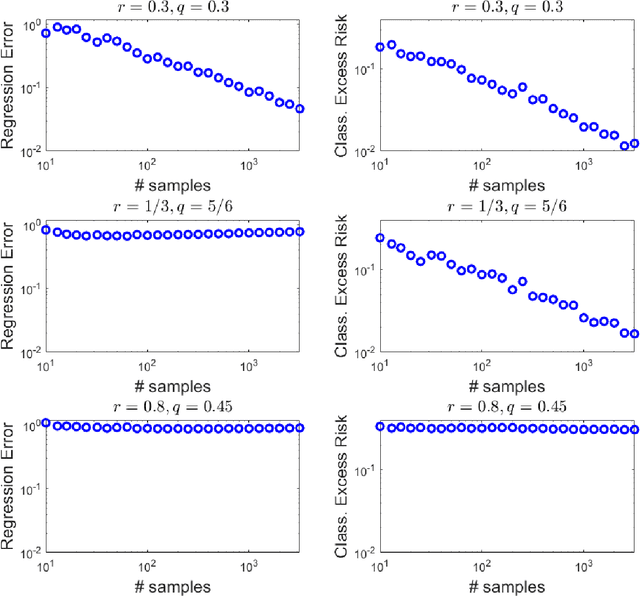
Overparametrized neural networks tend to perfectly fit noisy training data yet generalize well on test data. Inspired by this empirical observation, recent work has sought to understand this phenomenon of benign overfitting or harmless interpolation in the much simpler linear model. Previous theoretical work critically assumes that either the data features are statistically independent or the input data is high-dimensional; this precludes general nonparametric settings with structured feature maps. In this paper, we present a general and flexible framework for upper bounding regression and classification risk in a reproducing kernel Hilbert space. A key contribution is that our framework describes precise sufficient conditions on the data Gram matrix under which harmless interpolation occurs. Our results recover prior independent-features results (with a much simpler analysis), but they furthermore show that harmless interpolation can occur in more general settings such as features that are a bounded orthonormal system. Furthermore, our results show an asymptotic separation between classification and regression performance in a manner that was previously only shown for Gaussian features.

Low-rank matrix completion and denoising under Poisson noise

This paper considers the problem of estimating a low-rank matrix from the observation of all, or a subset, of its entries in the presence of Poisson noise. When we observe all the entries, this is a problem of matrix denoising; when we observe only a subset of the entries, this is a problem of matrix completion. In both cases, we exploit an assumption that the underlying matrix is low-rank. Specifically, we analyze several estimators, including a constrained nuclear-norm minimization program, nuclear-norm regularized least squares, and a nonconvex constrained low-rank optimization problem. We show that for all three estimators, with high probability, we have an upper error bound (in the Frobenius norm error metric) that depends on the matrix rank, the fraction of the elements observed, and maximal row and column sums of the true matrix. We furthermore show that the above results are minimax optimal (within a universal constant) in classes of matrices with low rank and bounded row and column sums. We also extend these results to handle the case of matrix multinomial denoising and completion.