What Can Natural Language Processing Do for Peer Review?

The number of scientific articles produced every year is growing rapidly. Providing quality control over them is crucial for scientists and, ultimately, for the public good. In modern science, this process is largely delegated to peer review -- a distributed procedure in which each submission is evaluated by several independent experts in the field. Peer review is widely used, yet it is hard, time-consuming, and prone to error. Since the artifacts involved in peer review -- manuscripts, reviews, discussions -- are largely text-based, Natural Language Processing has great potential to improve reviewing. As the emergence of large language models (LLMs) has enabled NLP assistance for many new tasks, the discussion on machine-assisted peer review is picking up the pace. Yet, where exactly is help needed, where can NLP help, and where should it stand aside? The goal of our paper is to provide a foundation for the future efforts in NLP for peer-reviewing assistance. We discuss peer review as a general process, exemplified by reviewing at AI conferences. We detail each step of the process from manuscript submission to camera-ready revision, and discuss the associated challenges and opportunities for NLP assistance, illustrated by existing work. We then turn to the big challenges in NLP for peer review as a whole, including data acquisition and licensing, operationalization and experimentation, and ethical issues. To help consolidate community efforts, we create a companion repository that aggregates key datasets pertaining to peer review. Finally, we issue a detailed call for action for the scientific community, NLP and AI researchers, policymakers, and funding bodies to help bring the research in NLP for peer review forward. We hope that our work will help set the agenda for research in machine-assisted scientific quality control in the age of AI, within the NLP community and beyond.

Perceptual adjustment queries and an inverted measurement paradigm for low-rank metric learning

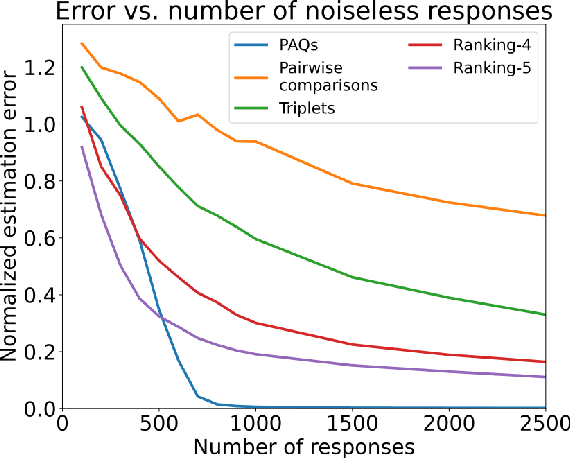
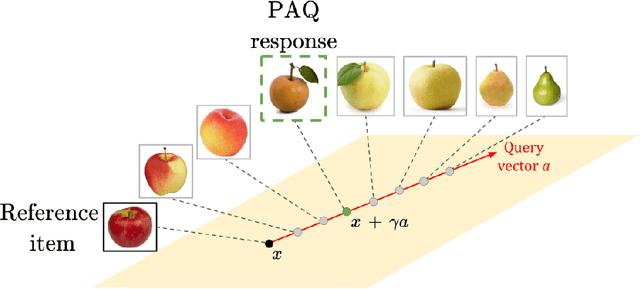
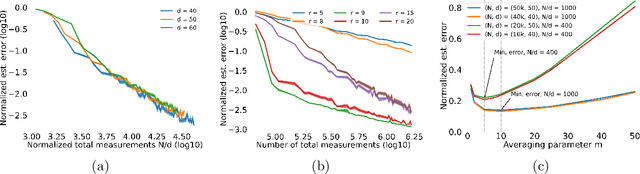
We introduce a new type of query mechanism for collecting human feedback, called the perceptual adjustment query ( PAQ). Being both informative and cognitively lightweight, the PAQ adopts an inverted measurement scheme, and combines advantages from both cardinal and ordinal queries. We showcase the PAQ in the metric learning problem, where we collect PAQ measurements to learn an unknown Mahalanobis distance. This gives rise to a high-dimensional, low-rank matrix estimation problem to which standard matrix estimators cannot be applied. Consequently, we develop a two-stage estimator for metric learning from PAQs, and provide sample complexity guarantees for this estimator. We present numerical simulations demonstrating the performance of the estimator and its notable properties.

A Bayesian Robust Regression Method for Corrupted Data Reconstruction

Because of the widespread existence of noise and data corruption, recovering the true regression parameters with a certain proportion of corrupted response variables is an essential task. Methods to overcome this problem often involve robust least-squares regression, but few methods perform well when confronted with severe adaptive adversarial attacks. In many applications, prior knowledge is often available from historical data or engineering experience, and by incorporating prior information into a robust regression method, we develop an effective robust regression method that can resist adaptive adversarial attacks. First, we propose the novel TRIP (hard Thresholding approach to Robust regression with sImple Prior) algorithm, which improves the breakdown point when facing adaptive adversarial attacks. Then, to improve the robustness and reduce the estimation error caused by the inclusion of priors, we use the idea of Bayesian reweighting to construct the more robust BRHT (robust Bayesian Reweighting regression via Hard Thresholding) algorithm. We prove the theoretical convergence of the proposed algorithms under mild conditions, and extensive experiments show that under different types of dataset attacks, our algorithms outperform other benchmark ones. Finally, we apply our methods to a data-recovery problem in a real-world application involving a space solar array, demonstrating their good applicability.

Allocation Schemes in Analytic Evaluation: Applicant-Centric Holistic or Attribute-Centric Segmented?

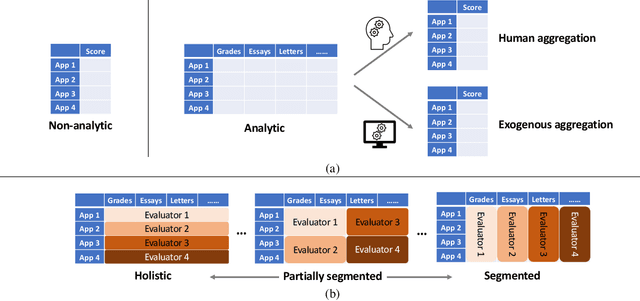
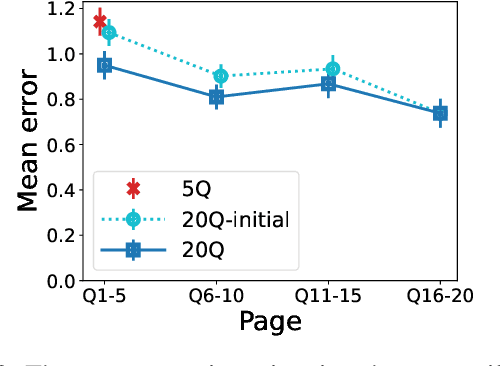
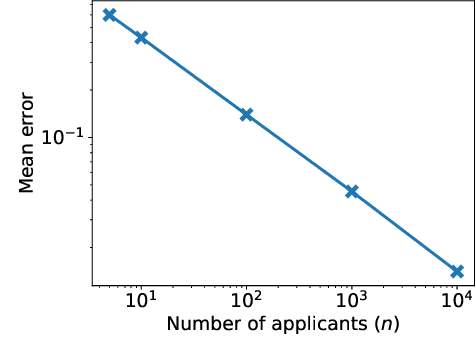
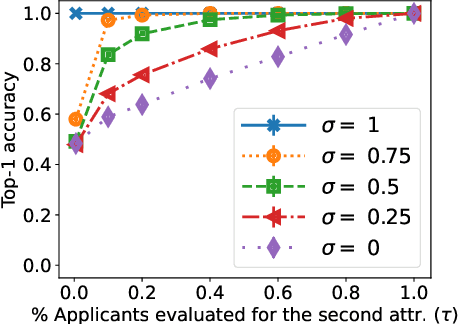
Many applications such as hiring and university admissions involve evaluation and selection of applicants. These tasks are fundamentally difficult, and require combining evidence from multiple different aspects (what we term "attributes"). In these applications, the number of applicants is often large, and a common practice is to assign the task to multiple evaluators in a distributed fashion. Specifically, in the often-used holistic allocation, each evaluator is assigned a subset of the applicants, and is asked to assess all relevant information for their assigned applicants. However, such an evaluation process is subject to issues such as miscalibration (evaluators see only a small fraction of the applicants and may not get a good sense of relative quality), and discrimination (evaluators are influenced by irrelevant information about the applicants). We identify that such attribute-based evaluation allows alternative allocation schemes. Specifically, we consider assigning each evaluator more applicants but fewer attributes per applicant, termed segmented allocation. We compare segmented allocation to holistic allocation on several dimensions via theoretical and experimental methods. We establish various tradeoffs between these two approaches, and identify conditions under which one approach results in more accurate evaluation than the other.

Modeling and Correcting Bias in Sequential Evaluation

We consider the problem of sequential evaluation, in which an evaluator observes candidates in a sequence and assigns scores to these candidates in an online, irrevocable fashion. Motivated by the psychology literature that has studied sequential bias in such settings -- namely, dependencies between the evaluation outcome and the order in which the candidates appear -- we propose a natural model for the evaluator's rating process that captures the lack of calibration inherent to such a task. We conduct crowdsourcing experiments to demonstrate various facets of our model. We then proceed to study how to correct sequential bias under our model by posing this as a statistical inference problem. We propose a near-linear time, online algorithm for this task and prove guarantees in terms of two canonical ranking metrics, matched with lower bounds demonstrating optimality in a certain sense. Our algorithm outperforms the de facto method of using the rankings induced by the reported scores.

Debiasing Evaluations That are Biased by Evaluations

It is common to evaluate a set of items by soliciting people to rate them. For example, universities ask students to rate the teaching quality of their instructors, and conference organizers ask authors of submissions to evaluate the quality of the reviews. However, in these applications, students often give a higher rating to a course if they receive higher grades in a course, and authors often give a higher rating to the reviews if their papers are accepted to the conference. In this work, we call these external factors the "outcome" experienced by people, and consider the problem of mitigating these outcome-induced biases in the given ratings when some information about the outcome is available. We formulate the information about the outcome as a known partial ordering on the bias. We propose a debiasing method by solving a regularized optimization problem under this ordering constraint, and also provide a carefully designed cross-validation method that adaptively chooses the appropriate amount of regularization. We provide theoretical guarantees on the performance of our algorithm, as well as experimental evaluations.

Stretching the Effectiveness of MLE from Accuracy to Bias for Pairwise Comparisons

A number of applications (e.g., AI bot tournaments, sports, peer grading, crowdsourcing) use pairwise comparison data and the Bradley-Terry-Luce (BTL) model to evaluate a given collection of items (e.g., bots, teams, students, search results). Past work has shown that under the BTL model, the widely-used maximum-likelihood estimator (MLE) is minimax-optimal in estimating the item parameters, in terms of the mean squared error. However, another important desideratum for designing estimators is fairness. In this work, we consider fairness modeled by the notion of bias in statistics. We show that the MLE incurs a suboptimal rate in terms of bias. We then propose a simple modification to the MLE, which "stretches" the bounding box of the maximum-likelihood optimizer by a small constant factor from the underlying ground truth domain. We show that this simple modification leads to an improved rate in bias, while maintaining minimax-optimality in the mean squared error. In this manner, our proposed class of estimators provably improves fairness represented by bias without loss in accuracy.

Your 2 is My 1, Your 3 is My 9: Handling Arbitrary Miscalibrations in Ratings

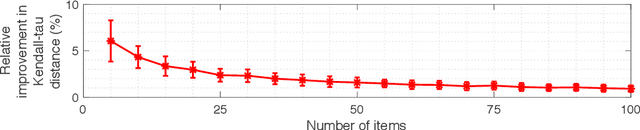
Cardinal scores (numeric ratings) collected from people are well known to suffer from miscalibrations. A popular approach to address this issue is to assume simplistic models of miscalibration (such as linear biases) to de-bias the scores. This approach, however, often fares poorly because people's miscalibrations are typically far more complex and not well understood. In the absence of simplifying assumptions on the miscalibration, it is widely believed by the crowdsourcing community that the only useful information in the cardinal scores is the induced ranking. In this paper, inspired by the framework of Stein's shrinkage, empirical Bayes, and the classic two-envelope problem, we contest this widespread belief. Specifically, we consider cardinal scores with arbitrary (or even adversarially chosen) miscalibrations which are only required to be consistent with the induced ranking. We design estimators which despite making no assumptions on the miscalibration, strictly and uniformly outperform all possible estimators that rely on only the ranking. Our estimators are flexible in that they can be used as a plug-in for a variety of applications, and we provide a proof-of-concept for A/B testing and ranking. Our results thus provide novel insights in the eternal debate between cardinal and ordinal data.

Image tag completion by local learning

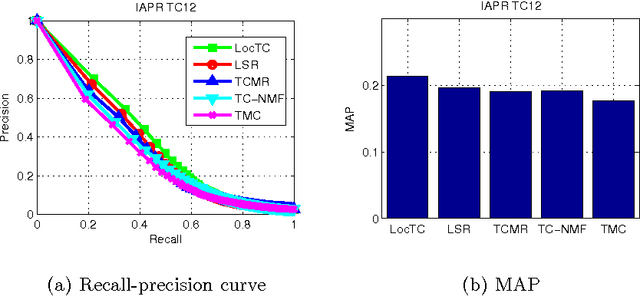
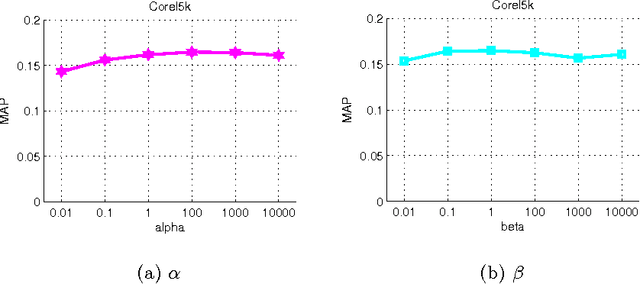
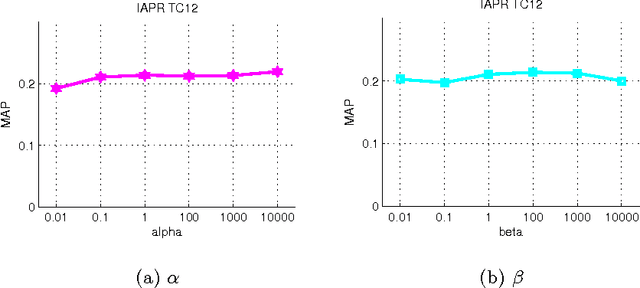
The problem of tag completion is to learn the missing tags of an image. In this paper, we propose to learn a tag scoring vector for each image by local linear learning. A local linear function is used in the neighborhood of each image to predict the tag scoring vectors of its neighboring images. We construct a unified objective function for the learning of both tag scoring vectors and local linear function parame- ters. In the objective, we impose the learned tag scoring vectors to be consistent with the known associations to the tags of each image, and also minimize the prediction error of each local linear function, while reducing the complexity of each local function. The objective function is optimized by an alternate optimization strategy and gradient descent methods in an iterative algorithm. We compare the proposed algorithm against different state-of-the-art tag completion methods, and the results show its advantages.

Representing data by sparse combination of contextual data points for classification

In this paper, we study the problem of using contextual da- ta points of a data point for its classification problem. We propose to represent a data point as the sparse linear reconstruction of its context, and learn the sparse context to gather with a linear classifier in a su- pervised way to increase its discriminative ability. We proposed a novel formulation for context learning, by modeling the learning of context reconstruction coefficients and classifier in a unified objective. In this objective, the reconstruction error is minimized and the coefficient spar- sity is encouraged. Moreover, the hinge loss of the classifier is minimized and the complexity of the classifier is reduced. This objective is opti- mized by an alternative strategy in an iterative algorithm. Experiments on three benchmark data set show its advantage over state-of-the-art context-based data representation and classification methods.