BiDepth Multimodal Neural Network: Bidirectional Depth Deep Learning Arcitecture for Spatial-Temporal Prediction

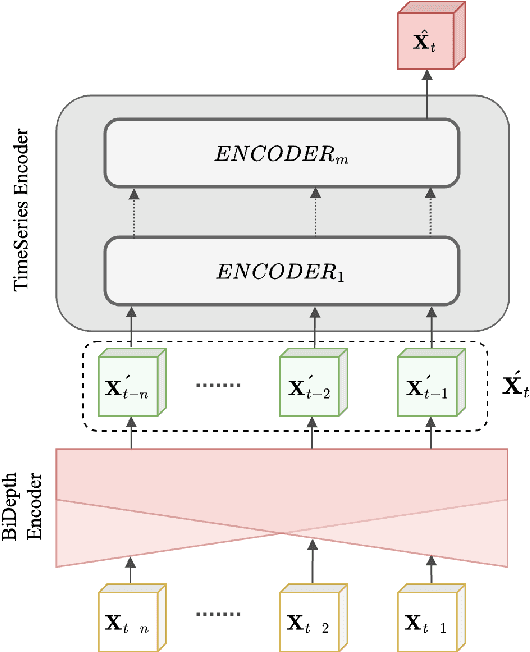
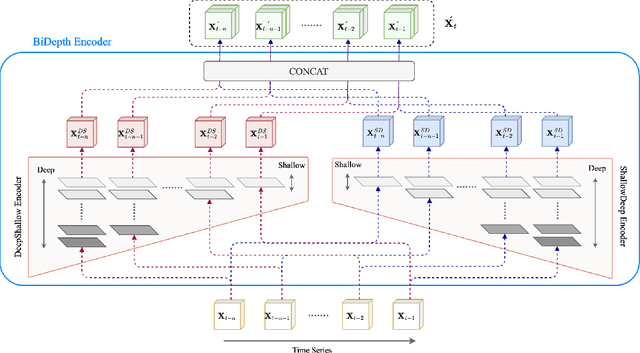
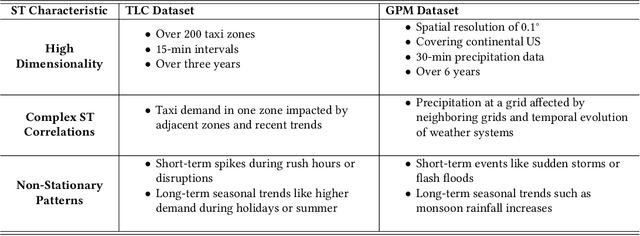
Accurate prediction of spatial-temporal (ST) information in dynamic systems, such as urban mobility and weather patterns, is a crucial yet challenging problem. The complexity stems from the intricate interplay between spatial proximity and temporal relevance, where both long-term trends and short-term fluctuations are present in convoluted patterns. Existing approaches, including traditional statistical methods and conventional neural networks, may provide inaccurate results due to the lack of an effective mechanism that simultaneously incorporates information at variable temporal depths while maintaining spatial context, resulting in a trade-off between comprehensive long-term historical analysis and responsiveness to short-term new information. To bridge this gap, this paper proposes the BiDepth Multimodal Neural Network (BDMNN) with bidirectional depth modulation that enables a comprehensive understanding of both long-term seasonality and short-term fluctuations, adapting to the complex ST context. Case studies with real-world public data demonstrate significant improvements in prediction accuracy, with a 12% reduction in Mean Squared Error for urban traffic prediction and a 15% improvement in rain precipitation forecasting compared to state-of-the-art benchmarks, without demanding extra computational resources.

Minimizing UCB: a Better Local Search Strategy in Local Bayesian Optimization

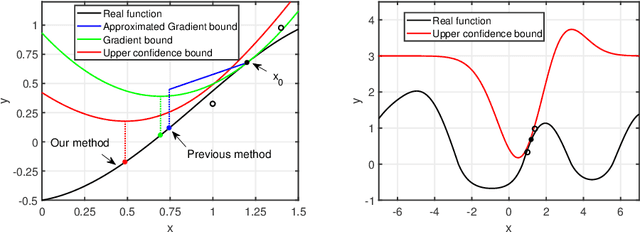
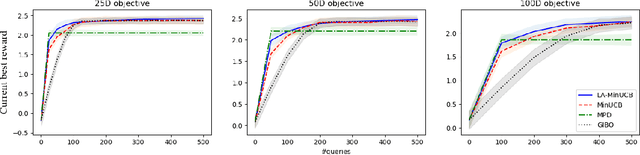
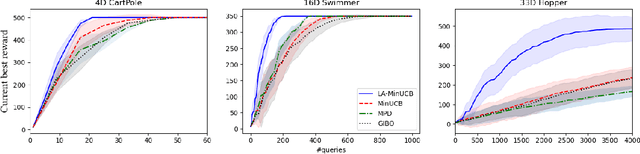
Local Bayesian optimization is a promising practical approach to solve the high dimensional black-box function optimization problem. Among them is the approximated gradient class of methods, which implements a strategy similar to gradient descent. These methods have achieved good experimental results and theoretical guarantees. However, given the distributional properties of the Gaussian processes applied on these methods, there may be potential to further exploit the information of the Gaussian processes to facilitate the BO search. In this work, we develop the relationship between the steps of the gradient descent method and one that minimizes the Upper Confidence Bound (UCB), and show that the latter can be a better strategy than direct gradient descent when a Gaussian process is applied as a surrogate. Through this insight, we propose a new local Bayesian optimization algorithm, MinUCB, which replaces the gradient descent step with minimizing UCB in GIBO. We further show that MinUCB maintains a similar convergence rate with GIBO. We then improve the acquisition function of MinUCB further through a look ahead strategy, and obtain a more efficient algorithm LA-MinUCB. We apply our algorithms on different synthetic and real-world functions, and the results show the effectiveness of our method. Our algorithms also illustrate improvements on local search strategies from an upper bound perspective in Bayesian optimization, and provides a new direction for future algorithm design.

A Novel Framework for Improving the Breakdown Point of Robust Regression Algorithms

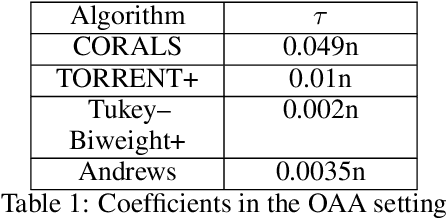
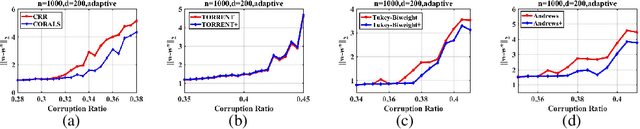
We present an effective framework for improving the breakdown point of robust regression algorithms. Robust regression has attracted widespread attention due to the ubiquity of outliers, which significantly affect the estimation results. However, many existing robust least-squares regression algorithms suffer from a low breakdown point, as they become stuck around local optima when facing severe attacks. By expanding on the previous work, we propose a novel framework that enhances the breakdown point of these algorithms by inserting a prior distribution in each iteration step, and adjusting the prior distribution according to historical information. We apply this framework to a specific algorithm and derive the consistent robust regression algorithm with iterative local search (CORALS). The relationship between CORALS and momentum gradient descent is described, and a detailed proof of the theoretical convergence of CORALS is presented. Finally, we demonstrate that the breakdown point of CORALS is indeed higher than that of the algorithm from which it is derived. We apply the proposed framework to other robust algorithms, and show that the improved algorithms achieve better results than the original algorithms, indicating the effectiveness of the proposed framework.

A Bayesian Robust Regression Method for Corrupted Data Reconstruction

Because of the widespread existence of noise and data corruption, recovering the true regression parameters with a certain proportion of corrupted response variables is an essential task. Methods to overcome this problem often involve robust least-squares regression, but few methods perform well when confronted with severe adaptive adversarial attacks. In many applications, prior knowledge is often available from historical data or engineering experience, and by incorporating prior information into a robust regression method, we develop an effective robust regression method that can resist adaptive adversarial attacks. First, we propose the novel TRIP (hard Thresholding approach to Robust regression with sImple Prior) algorithm, which improves the breakdown point when facing adaptive adversarial attacks. Then, to improve the robustness and reduce the estimation error caused by the inclusion of priors, we use the idea of Bayesian reweighting to construct the more robust BRHT (robust Bayesian Reweighting regression via Hard Thresholding) algorithm. We prove the theoretical convergence of the proposed algorithms under mild conditions, and extensive experiments show that under different types of dataset attacks, our algorithms outperform other benchmark ones. Finally, we apply our methods to a data-recovery problem in a real-world application involving a space solar array, demonstrating their good applicability.