A Novel Framework for Improving the Breakdown Point of Robust Regression Algorithms
Paper and Code
May 20, 2023
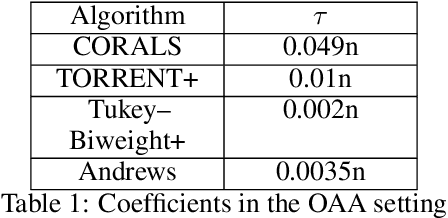
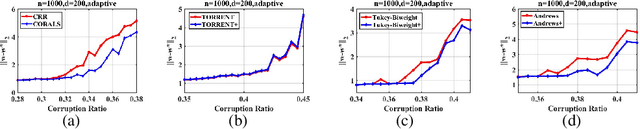

We present an effective framework for improving the breakdown point of robust regression algorithms. Robust regression has attracted widespread attention due to the ubiquity of outliers, which significantly affect the estimation results. However, many existing robust least-squares regression algorithms suffer from a low breakdown point, as they become stuck around local optima when facing severe attacks. By expanding on the previous work, we propose a novel framework that enhances the breakdown point of these algorithms by inserting a prior distribution in each iteration step, and adjusting the prior distribution according to historical information. We apply this framework to a specific algorithm and derive the consistent robust regression algorithm with iterative local search (CORALS). The relationship between CORALS and momentum gradient descent is described, and a detailed proof of the theoretical convergence of CORALS is presented. Finally, we demonstrate that the breakdown point of CORALS is indeed higher than that of the algorithm from which it is derived. We apply the proposed framework to other robust algorithms, and show that the improved algorithms achieve better results than the original algorithms, indicating the effectiveness of the proposed framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge