Minimizing UCB: a Better Local Search Strategy in Local Bayesian Optimization

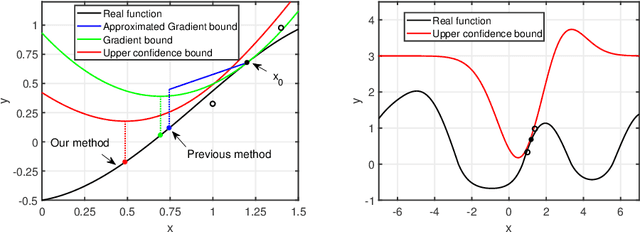
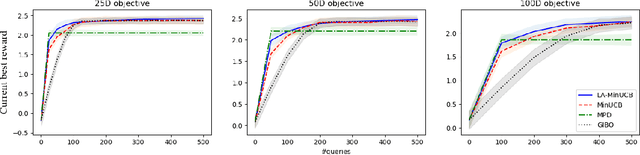
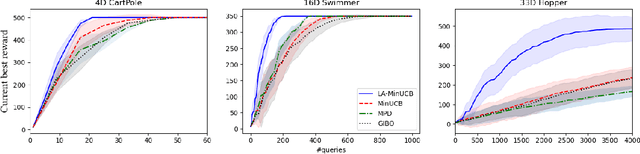
Local Bayesian optimization is a promising practical approach to solve the high dimensional black-box function optimization problem. Among them is the approximated gradient class of methods, which implements a strategy similar to gradient descent. These methods have achieved good experimental results and theoretical guarantees. However, given the distributional properties of the Gaussian processes applied on these methods, there may be potential to further exploit the information of the Gaussian processes to facilitate the BO search. In this work, we develop the relationship between the steps of the gradient descent method and one that minimizes the Upper Confidence Bound (UCB), and show that the latter can be a better strategy than direct gradient descent when a Gaussian process is applied as a surrogate. Through this insight, we propose a new local Bayesian optimization algorithm, MinUCB, which replaces the gradient descent step with minimizing UCB in GIBO. We further show that MinUCB maintains a similar convergence rate with GIBO. We then improve the acquisition function of MinUCB further through a look ahead strategy, and obtain a more efficient algorithm LA-MinUCB. We apply our algorithms on different synthetic and real-world functions, and the results show the effectiveness of our method. Our algorithms also illustrate improvements on local search strategies from an upper bound perspective in Bayesian optimization, and provides a new direction for future algorithm design.

Trajectory-Based Multi-Objective Hyperparameter Optimization for Model Retraining

Training machine learning models inherently involves a resource-intensive and noisy iterative learning procedure that allows epoch-wise monitoring of the model performance. However, in multi-objective hyperparameter optimization scenarios, the insights gained from the iterative learning procedure typically remain underutilized. We notice that tracking the model performance across multiple epochs under a hyperparameter setting creates a trajectory in the objective space and that trade-offs along the trajectories are often overlooked despite their potential to offer valuable insights to decision-making for model retraining. Therefore, in this study, we propose to enhance the multi-objective hyperparameter optimization problem by having training epochs as an additional decision variable to incorporate trajectory information. Correspondingly, we present a novel trajectory-based multi-objective Bayesian optimization algorithm characterized by two features: 1) an acquisition function that captures the improvement made by the predictive trajectory of any hyperparameter setting and 2) a multi-objective early stopping mechanism that determines when to terminate the trajectory to maximize epoch efficiency. Numerical experiments on diverse synthetic simulations and hyperparameter tuning benchmarks indicate that our algorithm outperforms the state-of-the-art multi-objective optimizers in both locating better trade-offs and tuning efficiency.

A Novel Framework for Improving the Breakdown Point of Robust Regression Algorithms

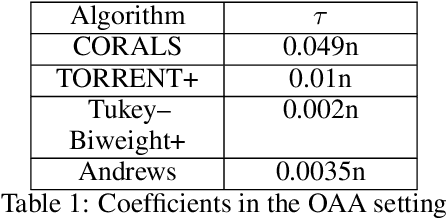
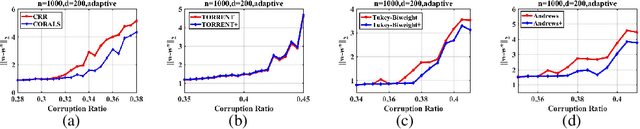
We present an effective framework for improving the breakdown point of robust regression algorithms. Robust regression has attracted widespread attention due to the ubiquity of outliers, which significantly affect the estimation results. However, many existing robust least-squares regression algorithms suffer from a low breakdown point, as they become stuck around local optima when facing severe attacks. By expanding on the previous work, we propose a novel framework that enhances the breakdown point of these algorithms by inserting a prior distribution in each iteration step, and adjusting the prior distribution according to historical information. We apply this framework to a specific algorithm and derive the consistent robust regression algorithm with iterative local search (CORALS). The relationship between CORALS and momentum gradient descent is described, and a detailed proof of the theoretical convergence of CORALS is presented. Finally, we demonstrate that the breakdown point of CORALS is indeed higher than that of the algorithm from which it is derived. We apply the proposed framework to other robust algorithms, and show that the improved algorithms achieve better results than the original algorithms, indicating the effectiveness of the proposed framework.

Adjusted Expected Improvement for Cumulative Regret Minimization in Noisy Bayesian Optimization

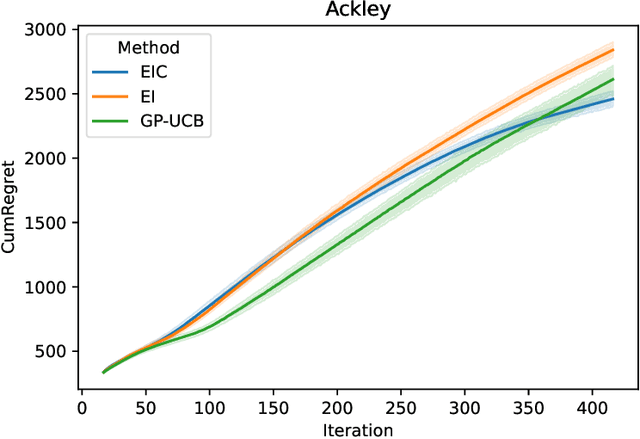
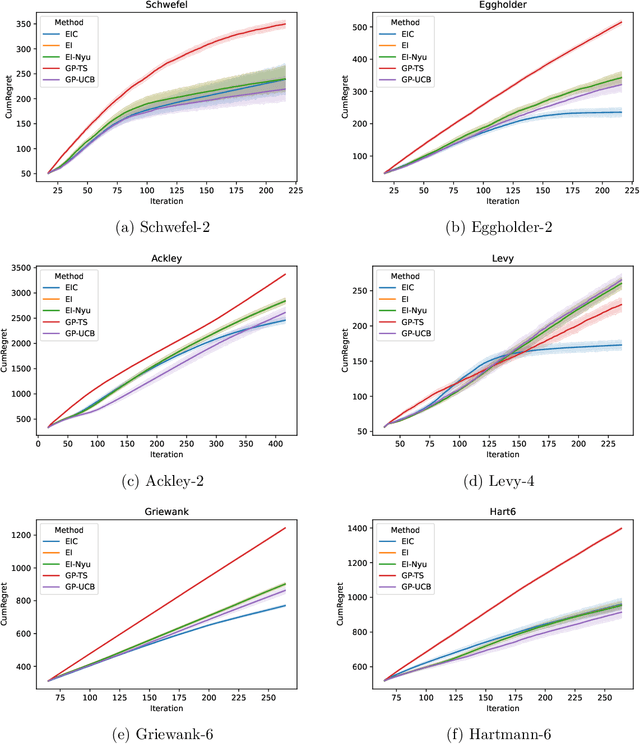
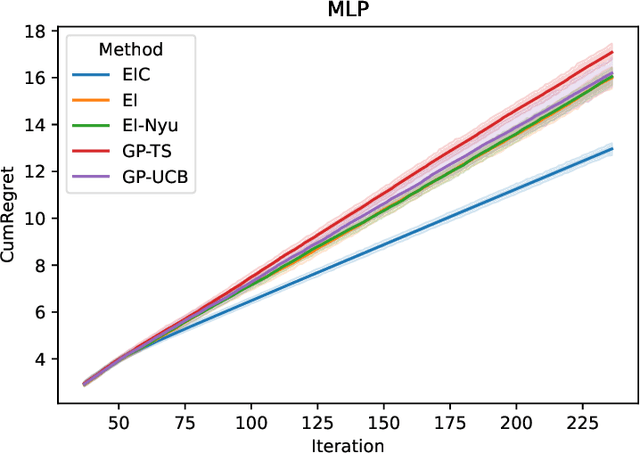
The expected improvement (EI) is one of the most popular acquisition functions for Bayesian optimization (BO) and has demonstrated good empirical performances in many applications for the minimization of simple regret. However, under the evaluation metric of cumulative regret, the performance of EI may not be competitive, and its existing theoretical regret upper bound still has room for improvement. To adapt the EI for better performance under cumulative regret, we introduce a novel quantity called the evaluation cost which is compared against the acquisition function, and with this, develop the expected improvement-cost (EIC) algorithm. In each iteration of EIC, a new point with the largest acquisition function value is sampled, only if that value exceeds its evaluation cost. If none meets this criteria, the current best point is resampled. This evaluation cost quantifies the potential downside of sampling a point, which is important under the cumulative regret metric as the objective function value in every iteration affects the performance measure. We further establish in theory a tight regret upper bound of EIC for the squared-exponential covariance kernel under mild regularity conditions, and perform experiments to illustrate the improvement of EIC over several popular BO algorithms.

A model aggregation approach for high-dimensional large-scale optimization

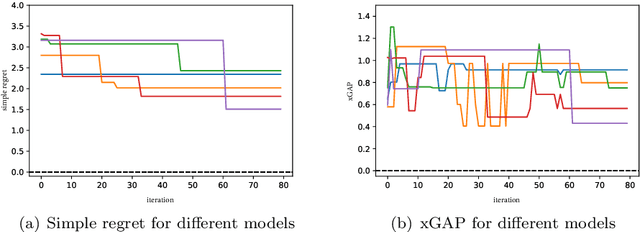
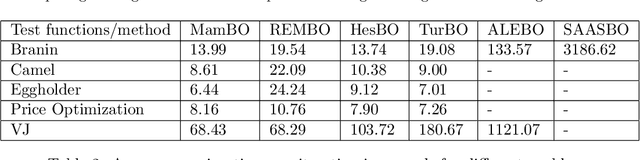
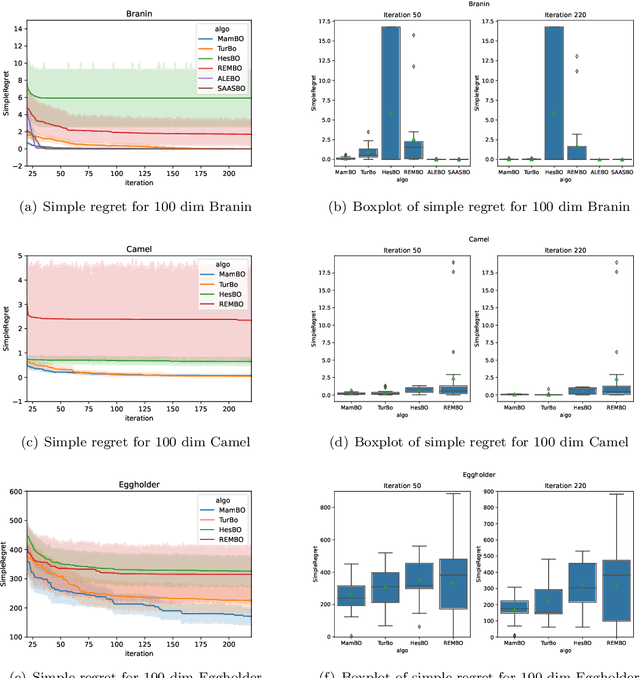
Bayesian optimization (BO) has been widely used in machine learning and simulation optimization. With the increase in computational resources and storage capacities in these fields, high-dimensional and large-scale problems are becoming increasingly common. In this study, we propose a model aggregation method in the Bayesian optimization (MamBO) algorithm for efficiently solving high-dimensional large-scale optimization problems. MamBO uses a combination of subsampling and subspace embeddings to collectively address high dimensionality and large-scale issues; in addition, a model aggregation method is employed to address the surrogate model uncertainty issue that arises when embedding is applied. This surrogate model uncertainty issue is largely ignored in the embedding literature and practice, and it is exacerbated when the problem is high-dimensional and data are limited. Our proposed model aggregation method reduces these lower-dimensional surrogate model risks and improves the robustness of the BO algorithm. We derive an asymptotic bound for the proposed aggregated surrogate model and prove the convergence of MamBO. Benchmark numerical experiments indicate that our algorithm achieves superior or comparable performance to other commonly used high-dimensional BO algorithms. Moreover, we apply MamBO to a cascade classifier of a machine learning algorithm for face detection, and the results reveal that MamBO finds settings that achieve higher classification accuracy than the benchmark settings and is computationally faster than other high-dimensional BO algorithms.

Combined Global and Local Search for Optimization with Gaussian Process Models

Gaussian process (GP) model based optimization is widely applied in simulation and machine learning. In general, it first estimates a GP model based on a few observations from the true response and then employs this model to guide the search, aiming to quickly locate the global optimum. Despite its successful applications, it has several limitations that may hinder its broader usage. First, building an accurate GP model can be difficult and computationally expensive, especially when the response function is multi-modal or varies significantly over the design space. Second, even with an appropriate model, the search process can be trapped in suboptimal regions before moving to the global optimum due to the excessive effort spent around the current best solution. In this work, we adopt the Additive Global and Local GP (AGLGP) model in the optimization framework. The model is rooted in the inducing-points-based GP sparse approximations and is combined with independent local models in different regions. With these properties, the AGLGP model is suitable for multi-modal responses with relatively large data sizes. Based on this AGLGP model, we propose a Combined Global and Local search for Optimization (CGLO) algorithm. It first divides the whole design space into disjoint local regions and identifies a promising region with the global model. Next, a local model in the selected region is fit to guide detailed search within this region. The algorithm then switches back to the global step when a good local solution is found. The global and local natures of CGLO enable it to enjoy the benefits of both global and local search to efficiently locate the global optimum.