Gated Adaptation for Continual Learning in Human Activity Recognition

Wearable sensors in Internet of Things (IoT) ecosystems increasingly support applications such as remote health monitoring, elderly care, and smart home automation, all of which rely on robust human activity recognition (HAR). Continual learning systems must balance plasticity (learning new tasks) with stability (retaining prior knowledge), yet AI models often exhibit catastrophic forgetting, where learning new tasks degrades performance on earlier ones. This challenge is especially acute in domain-incremental HAR, where on-device models must adapt to new subjects with distinct movement patterns while maintaining accuracy on prior subjects without transmitting sensitive data to the cloud. We propose a parameter-efficient continual learning framework based on channel-wise gated modulation of frozen pretrained representations. Our key insight is that adaptation should operate through feature selection rather than feature generation: by restricting learned transformations to diagonal scaling of existing features, we preserve the geometry of pretrained representations while enabling subject-specific modulation. We provide a theoretical analysis showing that gating implements a bounded diagonal operator that limits representational drift compared to unconstrained linear transformations. Empirically, freezing the backbone substantially reduces forgetting, and lightweight gates restore lost adaptation capacity, achieving stability and plasticity simultaneously. On PAMAP2 with 8 sequential subjects, our approach reduces forgetting from 39.7% to 16.2% and improves final accuracy from 56.7% to 77.7%, while training less than 2% of parameters. Our method matches or exceeds standard continual learning baselines without replay buffers or task-specific regularization, confirming that structured diagonal operators are effective and efficient under distribution shift.

Brownian Bridge Augmented Surrogate Simulation and Injection Planning for Geological CO$_2$ Storage

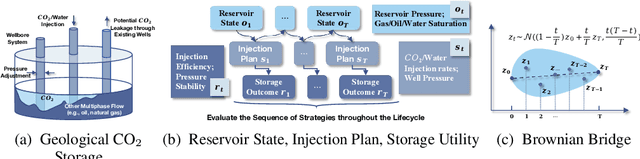
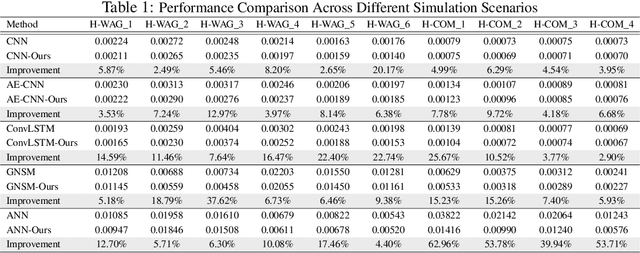
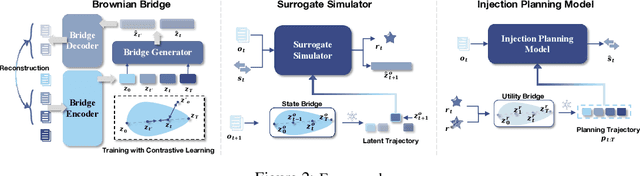
Geological CO2 storage (GCS) involves injecting captured CO2 into deep subsurface formations to support climate goals. The effective management of GCS relies on adaptive injection planning to dynamically control injection rates and well pressures to balance both storage safety and efficiency. Prior literature, including numerical optimization methods and surrogate-optimization methods, is limited by real-world GCS requirements of smooth state transitions and goal-directed planning within limited time. To address these limitations, we propose a Brownian Bridge-augmented framework for surrogate simulation and injection planning in GCS and develop two insights: (i) Brownian bridge as a smooth state regularizer for better surrogate simulation; (ii) Brownian bridge as goal-time-conditioned planning guidance for improved injection planning. Our method has three stages: (i) learning deep Brownian bridge representations with contrastive and reconstructive losses from historical reservoir and utility trajectories, (ii) incorporating Brownian bridge-based next state interpolation for simulator regularization, and (iii) guiding injection planning with Brownian utility-conditioned trajectories to generate high-quality injection plans. Experimental results across multiple datasets collected from diverse GCS settings demonstrate that our framework consistently improves simulation fidelity and planning effectiveness while maintaining low computational overhead.

Guiding Diffusion with Deep Geometric Moments: Balancing Fidelity and Variation

Text-to-image generation models have achieved remarkable capabilities in synthesizing images, but often struggle to provide fine-grained control over the output. Existing guidance approaches, such as segmentation maps and depth maps, introduce spatial rigidity that restricts the inherent diversity of diffusion models. In this work, we introduce Deep Geometric Moments (DGM) as a novel form of guidance that encapsulates the subject's visual features and nuances through a learned geometric prior. DGMs focus specifically on the subject itself compared to DINO or CLIP features, which suffer from overemphasis on global image features or semantics. Unlike ResNets, which are sensitive to pixel-wise perturbations, DGMs rely on robust geometric moments. Our experiments demonstrate that DGM effectively balance control and diversity in diffusion-based image generation, allowing a flexible control mechanism for steering the diffusion process.

POCAII: Parameter Optimization with Conscious Allocation using Iterative Intelligence

In this paper we propose for the first time the hyperparameter optimization (HPO) algorithm POCAII. POCAII differs from the Hyperband and Successive Halving literature by explicitly separating the search and evaluation phases and utilizing principled approaches to exploration and exploitation principles during both phases. Such distinction results in a highly flexible scheme for managing a hyperparameter optimization budget by focusing on search (i.e., generating competing configurations) towards the start of the HPO process while increasing the evaluation effort as the HPO comes to an end. POCAII was compared to state of the art approaches SMAC, BOHB and DEHB. Our algorithm shows superior performance in low-budget hyperparameter optimization regimes. Since many practitioners do not have exhaustive resources to assign to HPO, it has wide applications to real-world problems. Moreover, the empirical evidence showed how POCAII demonstrates higher robustness and lower variance in the results. This is again very important when considering realistic scenarios with extremely expensive models to train.

Parameter Optimization with Conscious Allocation (POCA)

The performance of modern machine learning algorithms depends upon the selection of a set of hyperparameters. Common examples of hyperparameters are learning rate and the number of layers in a dense neural network. Auto-ML is a branch of optimization that has produced important contributions in this area. Within Auto-ML, hyperband-based approaches, which eliminate poorly-performing configurations after evaluating them at low budgets, are among the most effective. However, the performance of these algorithms strongly depends on how effectively they allocate the computational budget to various hyperparameter configurations. We present the new Parameter Optimization with Conscious Allocation (POCA), a hyperband-based algorithm that adaptively allocates the inputted budget to the hyperparameter configurations it generates following a Bayesian sampling scheme. We compare POCA to its nearest competitor at optimizing the hyperparameters of an artificial toy function and a deep neural network and find that POCA finds strong configurations faster in both settings.

A model aggregation approach for high-dimensional large-scale optimization

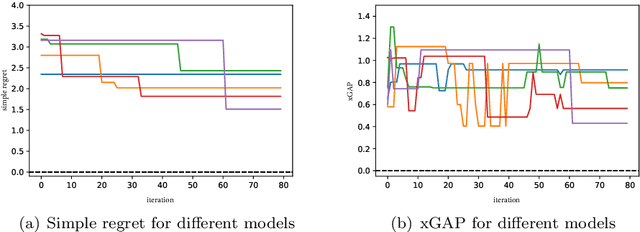
Bayesian optimization (BO) has been widely used in machine learning and simulation optimization. With the increase in computational resources and storage capacities in these fields, high-dimensional and large-scale problems are becoming increasingly common. In this study, we propose a model aggregation method in the Bayesian optimization (MamBO) algorithm for efficiently solving high-dimensional large-scale optimization problems. MamBO uses a combination of subsampling and subspace embeddings to collectively address high dimensionality and large-scale issues; in addition, a model aggregation method is employed to address the surrogate model uncertainty issue that arises when embedding is applied. This surrogate model uncertainty issue is largely ignored in the embedding literature and practice, and it is exacerbated when the problem is high-dimensional and data are limited. Our proposed model aggregation method reduces these lower-dimensional surrogate model risks and improves the robustness of the BO algorithm. We derive an asymptotic bound for the proposed aggregated surrogate model and prove the convergence of MamBO. Benchmark numerical experiments indicate that our algorithm achieves superior or comparable performance to other commonly used high-dimensional BO algorithms. Moreover, we apply MamBO to a cascade classifier of a machine learning algorithm for face detection, and the results reveal that MamBO finds settings that achieve higher classification accuracy than the benchmark settings and is computationally faster than other high-dimensional BO algorithms.

Part-X: A Family of Stochastic Algorithms for Search-Based Test Generation with Probabilistic Guarantees

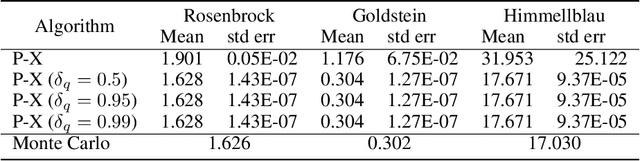
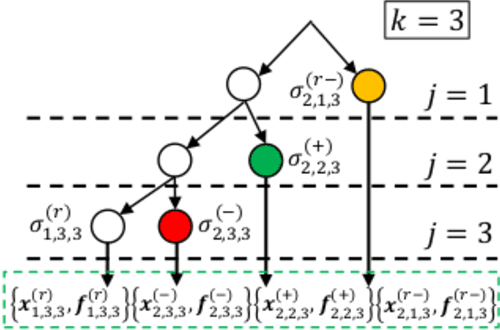
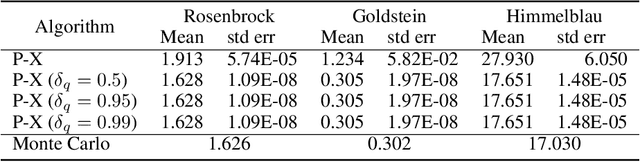
Requirements driven search-based testing (also known as falsification) has proven to be a practical and effective method for discovering erroneous behaviors in Cyber-Physical Systems. Despite the constant improvements on the performance and applicability of falsification methods, they all share a common characteristic. Namely, they are best-effort methods which do not provide any guarantees on the absence of erroneous behaviors (falsifiers) when the testing budget is exhausted. The absence of finite time guarantees is a major limitation which prevents falsification methods from being utilized in certification procedures. In this paper, we address the finite-time guarantees problem by developing a new stochastic algorithm. Our proposed algorithm not only estimates (bounds) the probability that falsifying behaviors exist, but also it identifies the regions where these falsifying behaviors may occur. We demonstrate the applicability of our approach on standard benchmark functions from the optimization literature and on the F16 benchmark problem.