Ercong Zhang
A model aggregation approach for high-dimensional large-scale optimization
May 16, 2022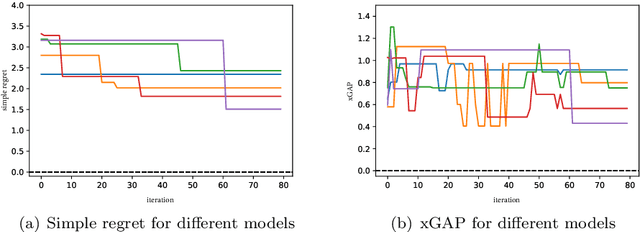
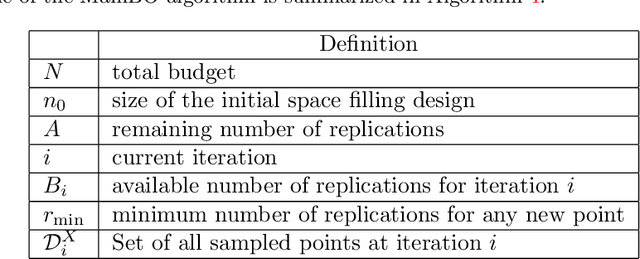
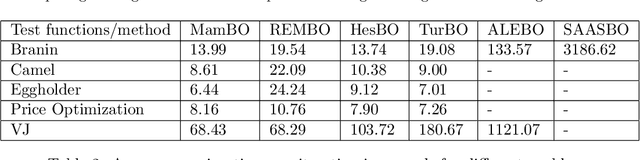
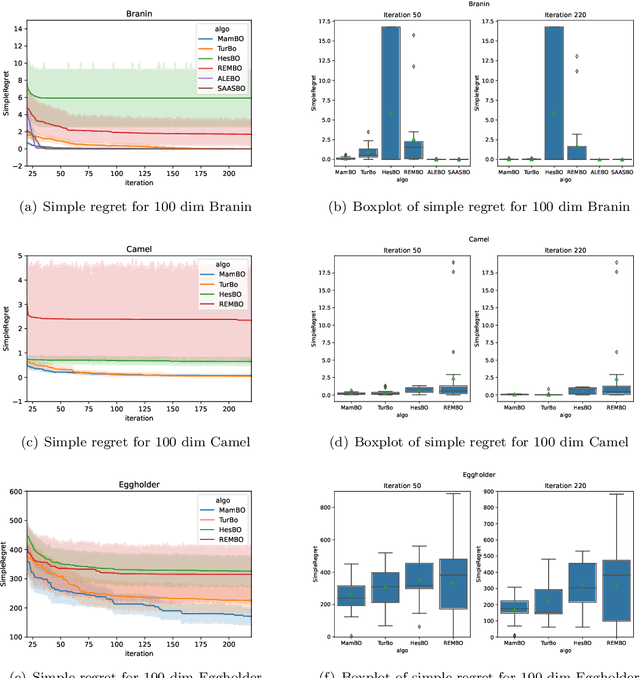
Abstract:Bayesian optimization (BO) has been widely used in machine learning and simulation optimization. With the increase in computational resources and storage capacities in these fields, high-dimensional and large-scale problems are becoming increasingly common. In this study, we propose a model aggregation method in the Bayesian optimization (MamBO) algorithm for efficiently solving high-dimensional large-scale optimization problems. MamBO uses a combination of subsampling and subspace embeddings to collectively address high dimensionality and large-scale issues; in addition, a model aggregation method is employed to address the surrogate model uncertainty issue that arises when embedding is applied. This surrogate model uncertainty issue is largely ignored in the embedding literature and practice, and it is exacerbated when the problem is high-dimensional and data are limited. Our proposed model aggregation method reduces these lower-dimensional surrogate model risks and improves the robustness of the BO algorithm. We derive an asymptotic bound for the proposed aggregated surrogate model and prove the convergence of MamBO. Benchmark numerical experiments indicate that our algorithm achieves superior or comparable performance to other commonly used high-dimensional BO algorithms. Moreover, we apply MamBO to a cascade classifier of a machine learning algorithm for face detection, and the results reveal that MamBO finds settings that achieve higher classification accuracy than the benchmark settings and is computationally faster than other high-dimensional BO algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge