An Adaptive Dimension Reduction Estimation Method for High-dimensional Bayesian Optimization

Bayesian optimization (BO) has shown impressive results in a variety of applications within low-to-moderate dimensional Euclidean spaces. However, extending BO to high-dimensional settings remains a significant challenge. We address this challenge by proposing a two-step optimization framework. Initially, we identify the effective dimension reduction (EDR) subspace for the objective function using the minimum average variance estimation (MAVE) method. Subsequently, we construct a Gaussian process model within this EDR subspace and optimize it using the expected improvement criterion. Our algorithm offers the flexibility to operate these steps either concurrently or in sequence. In the sequential approach, we meticulously balance the exploration-exploitation trade-off by distributing the sampling budget between subspace estimation and function optimization, and the convergence rate of our algorithm in high-dimensional contexts has been established. Numerical experiments validate the efficacy of our method in challenging scenarios.

Adjusted Expected Improvement for Cumulative Regret Minimization in Noisy Bayesian Optimization

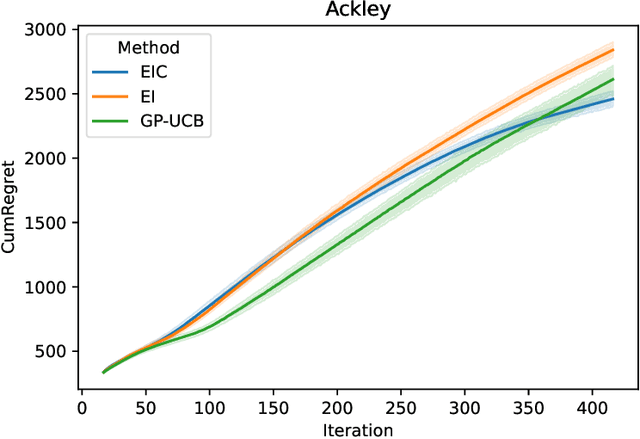
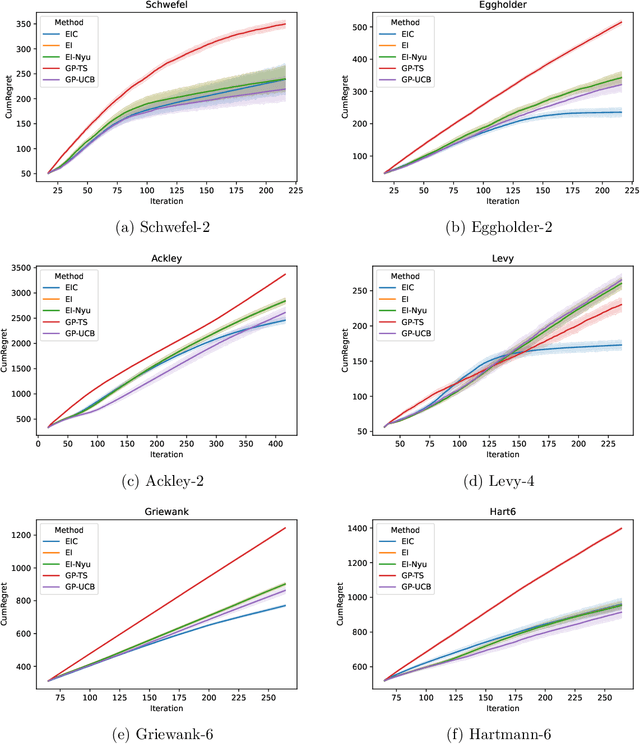
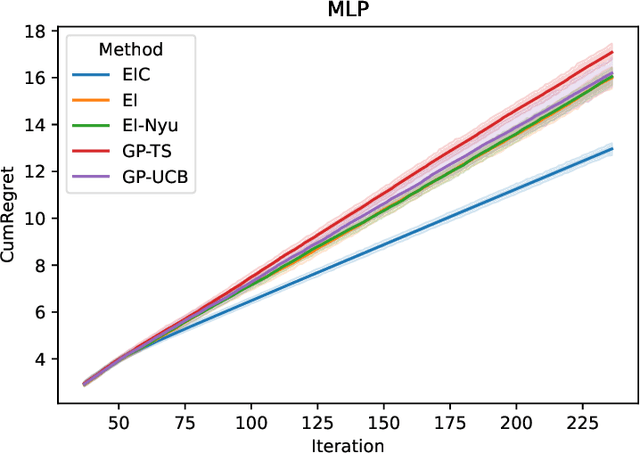
The expected improvement (EI) is one of the most popular acquisition functions for Bayesian optimization (BO) and has demonstrated good empirical performances in many applications for the minimization of simple regret. However, under the evaluation metric of cumulative regret, the performance of EI may not be competitive, and its existing theoretical regret upper bound still has room for improvement. To adapt the EI for better performance under cumulative regret, we introduce a novel quantity called the evaluation cost which is compared against the acquisition function, and with this, develop the expected improvement-cost (EIC) algorithm. In each iteration of EIC, a new point with the largest acquisition function value is sampled, only if that value exceeds its evaluation cost. If none meets this criteria, the current best point is resampled. This evaluation cost quantifies the potential downside of sampling a point, which is important under the cumulative regret metric as the objective function value in every iteration affects the performance measure. We further establish in theory a tight regret upper bound of EIC for the squared-exponential covariance kernel under mild regularity conditions, and perform experiments to illustrate the improvement of EIC over several popular BO algorithms.

Infinite Arms Bandit: Optimality via Confidence Bounds

The infinite arms bandit problem was initiated by Berry et al. (1997). They derived a regret lower bound of all solutions for Bernoulli rewards, and proposed various bandit strategies based on success runs, but which do not achieve this bound. We propose here a confidence bound target (CBT) algorithm that achieves extensions of their regret lower bound for general reward distributions and distribution priors. The algorithm does not require information on the reward distributions, for each arm we require only the mean and standard deviation of its rewards to compute a confidence bound. We play the arm with the smallest confidence bound provided it is smaller than a target mean. If the confidence bounds are all larger, then we play a new arm. We show how the target mean can be computed from the prior so that the smallest asymptotic regret, among all infinite arms bandit algorithms, is achieved. We also show that in the absence of information on the prior, the target mean can be determined empirically, and that the regret achieved is comparable to the smallest regret. Numerical studies show that CBT is versatile and outperforms its competitors.