Gradient-based Sample Selection for Faster Bayesian Optimization

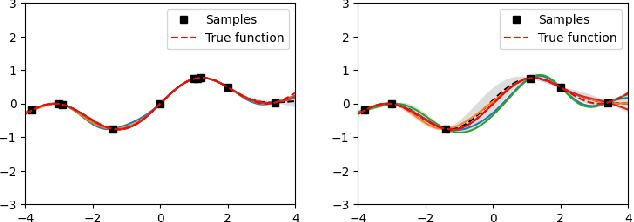
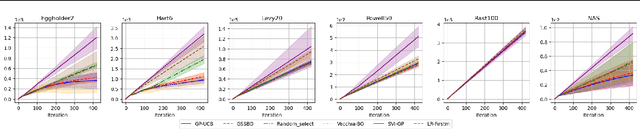
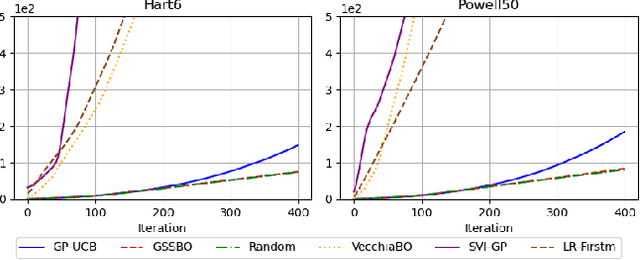
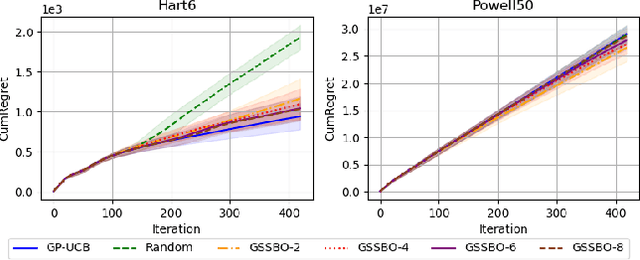
Bayesian optimization (BO) is an effective technique for black-box optimization. However, its applicability is typically limited to moderate-budget problems due to the cubic complexity in computing the Gaussian process (GP) surrogate model. In large-budget scenarios, directly employing the standard GP model faces significant challenges in computational time and resource requirements. In this paper, we propose a novel approach, gradient-based sample selection Bayesian Optimization (GSSBO), to enhance the computational efficiency of BO. The GP model is constructed on a selected set of samples instead of the whole dataset. These samples are selected by leveraging gradient information to maintain diversity and representation. We provide a theoretical analysis of the gradient-based sample selection strategy and obtain explicit sublinear regret bounds for our proposed framework. Extensive experiments on synthetic and real-world tasks demonstrate that our approach significantly reduces the computational cost of GP fitting in BO while maintaining optimization performance comparable to baseline methods.

Weighted Euclidean Distance Matrices over Mixed Continuous and Categorical Inputs for Gaussian Process Models

Gaussian Process (GP) models are widely utilized as surrogate models in scientific and engineering fields. However, standard GP models are limited to continuous variables due to the difficulties in establishing correlation structures for categorical variables. To overcome this limitati on, we introduce WEighted Euclidean distance matrices Gaussian Process (WEGP). WEGP constructs the kernel function for each categorical input by estimating the Euclidean distance matrix (EDM) among all categorical choices of this input. The EDM is represented as a linear combination of several predefined base EDMs, each scaled by a positive weight. The weights, along with other kernel hyperparameters, are inferred using a fully Bayesian framework. We analyze the predictive performance of WEGP theoretically. Numerical experiments validate the accuracy of our GP model, and by WEGP, into Bayesian Optimization (BO), we achieve superior performance on both synthetic and real-world optimization problems.

Combined Global and Local Search for Optimization with Gaussian Process Models

Gaussian process (GP) model based optimization is widely applied in simulation and machine learning. In general, it first estimates a GP model based on a few observations from the true response and then employs this model to guide the search, aiming to quickly locate the global optimum. Despite its successful applications, it has several limitations that may hinder its broader usage. First, building an accurate GP model can be difficult and computationally expensive, especially when the response function is multi-modal or varies significantly over the design space. Second, even with an appropriate model, the search process can be trapped in suboptimal regions before moving to the global optimum due to the excessive effort spent around the current best solution. In this work, we adopt the Additive Global and Local GP (AGLGP) model in the optimization framework. The model is rooted in the inducing-points-based GP sparse approximations and is combined with independent local models in different regions. With these properties, the AGLGP model is suitable for multi-modal responses with relatively large data sizes. Based on this AGLGP model, we propose a Combined Global and Local search for Optimization (CGLO) algorithm. It first divides the whole design space into disjoint local regions and identifies a promising region with the global model. Next, a local model in the selected region is fit to guide detailed search within this region. The algorithm then switches back to the global step when a good local solution is found. The global and local natures of CGLO enable it to enjoy the benefits of both global and local search to efficiently locate the global optimum.