Minimizing UCB: a Better Local Search Strategy in Local Bayesian Optimization
Paper and Code
May 24, 2024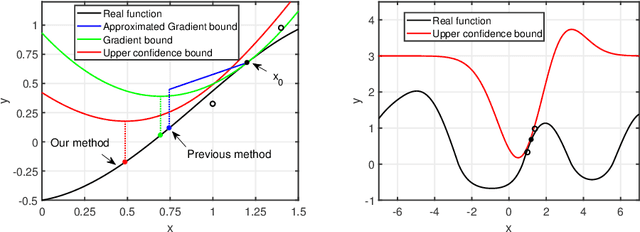
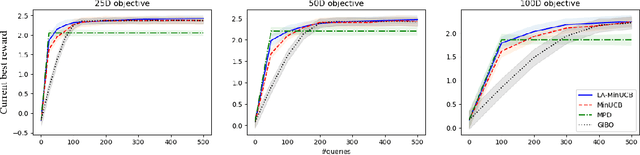
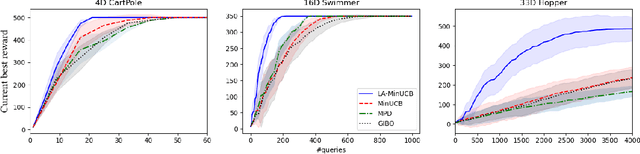
Local Bayesian optimization is a promising practical approach to solve the high dimensional black-box function optimization problem. Among them is the approximated gradient class of methods, which implements a strategy similar to gradient descent. These methods have achieved good experimental results and theoretical guarantees. However, given the distributional properties of the Gaussian processes applied on these methods, there may be potential to further exploit the information of the Gaussian processes to facilitate the BO search. In this work, we develop the relationship between the steps of the gradient descent method and one that minimizes the Upper Confidence Bound (UCB), and show that the latter can be a better strategy than direct gradient descent when a Gaussian process is applied as a surrogate. Through this insight, we propose a new local Bayesian optimization algorithm, MinUCB, which replaces the gradient descent step with minimizing UCB in GIBO. We further show that MinUCB maintains a similar convergence rate with GIBO. We then improve the acquisition function of MinUCB further through a look ahead strategy, and obtain a more efficient algorithm LA-MinUCB. We apply our algorithms on different synthetic and real-world functions, and the results show the effectiveness of our method. Our algorithms also illustrate improvements on local search strategies from an upper bound perspective in Bayesian optimization, and provides a new direction for future algorithm design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge