HITSnDIFFs: From Truth Discovery to Ability Discovery by Recovering Matrices with the Consecutive Ones Property

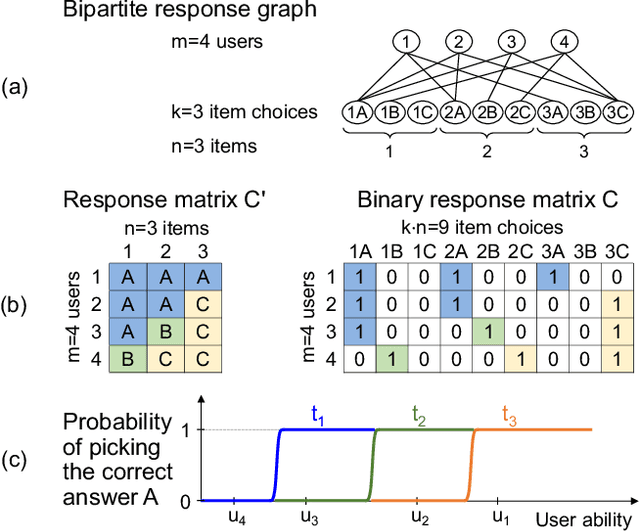
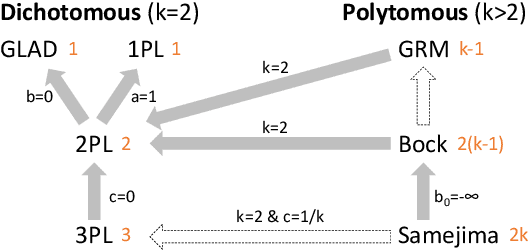
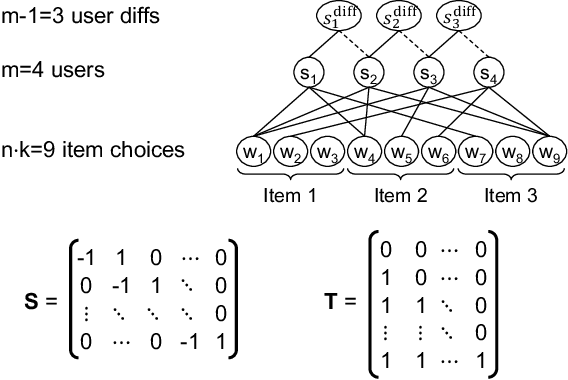
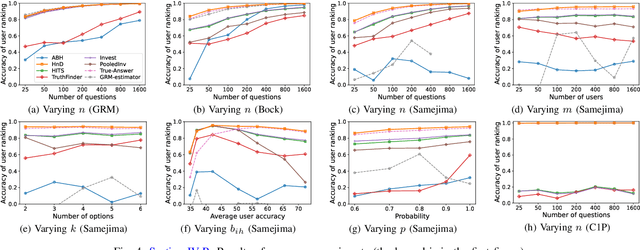
We analyze a general problem in a crowd-sourced setting where one user asks a question (also called item) and other users return answers (also called labels) for this question. Different from existing crowd sourcing work which focuses on finding the most appropriate label for the question (the "truth"), our problem is to determine a ranking of the users based on their ability to answer questions. We call this problem "ability discovery" to emphasize the connection to and duality with the more well-studied problem of "truth discovery". To model items and their labels in a principled way, we draw upon Item Response Theory (IRT) which is the widely accepted theory behind standardized tests such as SAT and GRE. We start from an idealized setting where the relative performance of users is consistent across items and better users choose better fitting labels for each item. We posit that a principled algorithmic solution to our more general problem should solve this ideal setting correctly and observe that the response matrices in this setting obey the Consecutive Ones Property (C1P). While C1P is well understood algorithmically with various discrete algorithms, we devise a novel variant of the HITS algorithm which we call "HITSNDIFFS" (or HND), and prove that it can recover the ideal C1P-permutation in case it exists. Unlike fast combinatorial algorithms for finding the consecutive ones permutation (if it exists), HND also returns an ordering when such a permutation does not exist. Thus it provides a principled heuristic for our problem that is guaranteed to return the correct answer in the ideal setting. Our experiments show that HND produces user rankings with robustly high accuracy compared to state-of-the-art truth discovery methods. We also show that our novel variant of HITS scales better in the number of users than ABH, the only prior spectral C1P reconstruction algorithm.

Allocation Schemes in Analytic Evaluation: Applicant-Centric Holistic or Attribute-Centric Segmented?

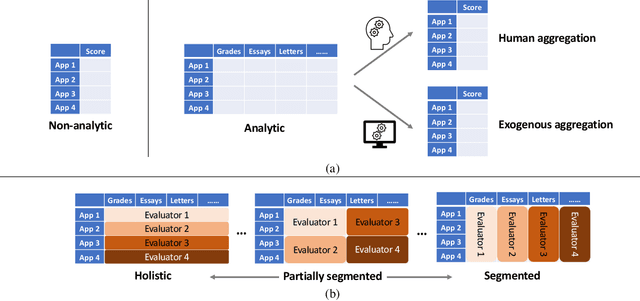
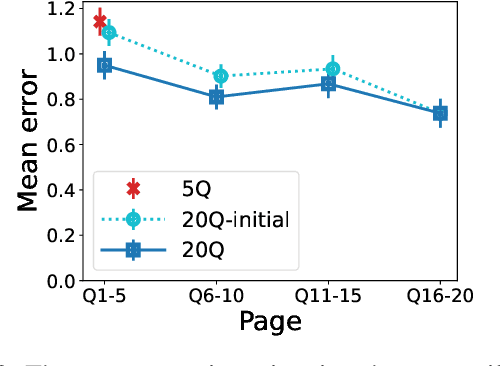
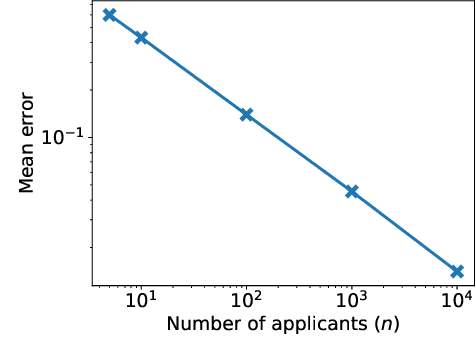
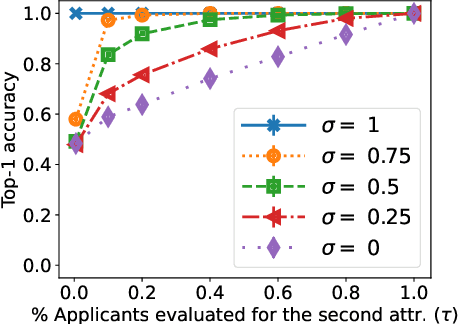
Many applications such as hiring and university admissions involve evaluation and selection of applicants. These tasks are fundamentally difficult, and require combining evidence from multiple different aspects (what we term "attributes"). In these applications, the number of applicants is often large, and a common practice is to assign the task to multiple evaluators in a distributed fashion. Specifically, in the often-used holistic allocation, each evaluator is assigned a subset of the applicants, and is asked to assess all relevant information for their assigned applicants. However, such an evaluation process is subject to issues such as miscalibration (evaluators see only a small fraction of the applicants and may not get a good sense of relative quality), and discrimination (evaluators are influenced by irrelevant information about the applicants). We identify that such attribute-based evaluation allows alternative allocation schemes. Specifically, we consider assigning each evaluator more applicants but fewer attributes per applicant, termed segmented allocation. We compare segmented allocation to holistic allocation on several dimensions via theoretical and experimental methods. We establish various tradeoffs between these two approaches, and identify conditions under which one approach results in more accurate evaluation than the other.