Wolfgang Gatterbauer
Database Views as Explanations for Relational Deep Learning
Sep 11, 2025Abstract:In recent years, there has been significant progress in the development of deep learning models over relational databases, including architectures based on heterogeneous graph neural networks (hetero-GNNs) and heterogeneous graph transformers. In effect, such architectures state how the database records and links (e.g., foreign-key references) translate into a large, complex numerical expression, involving numerous learnable parameters. This complexity makes it hard to explain, in human-understandable terms, how a model uses the available data to arrive at a given prediction. We present a novel framework for explaining machine-learning models over relational databases, where explanations are view definitions that highlight focused parts of the database that mostly contribute to the model's prediction. We establish such global abductive explanations by adapting the classic notion of determinacy by Nash, Segoufin, and Vianu (2010). In addition to tuning the tradeoff between determinacy and conciseness, the framework allows controlling the level of granularity by adopting different fragments of view definitions, such as ones highlighting whole columns, foreign keys between tables, relevant groups of tuples, and so on. We investigate the realization of the framework in the case of hetero-GNNs. We develop heuristic algorithms that avoid the exhaustive search over the space of all databases. We propose techniques that are model-agnostic, and others that are tailored to hetero-GNNs via the notion of learnable masking. Our approach is evaluated through an extensive empirical study on the RelBench collection, covering a variety of domains and different record-level tasks. The results demonstrate the usefulness of the proposed explanations, as well as the efficiency of their generation.
HITSnDIFFs: From Truth Discovery to Ability Discovery by Recovering Matrices with the Consecutive Ones Property
Dec 21, 2023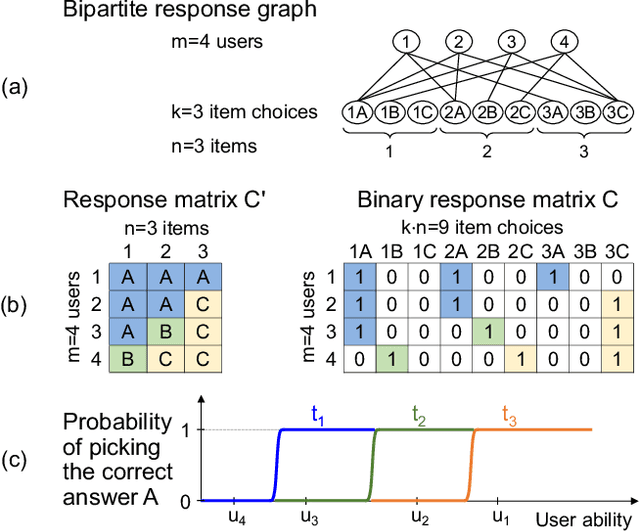
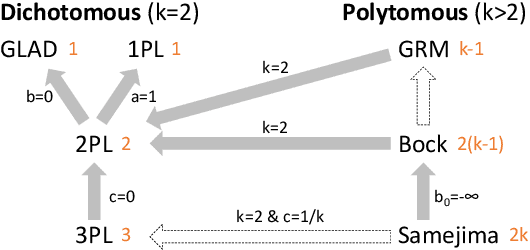
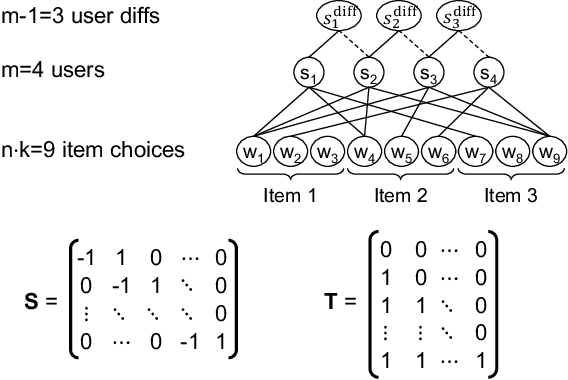
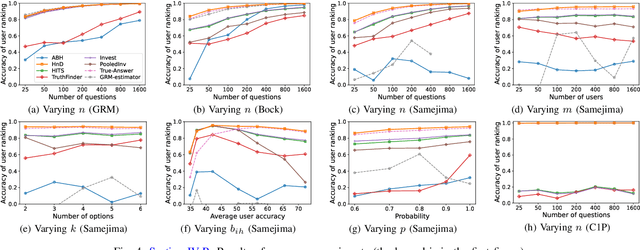
Abstract:We analyze a general problem in a crowd-sourced setting where one user asks a question (also called item) and other users return answers (also called labels) for this question. Different from existing crowd sourcing work which focuses on finding the most appropriate label for the question (the "truth"), our problem is to determine a ranking of the users based on their ability to answer questions. We call this problem "ability discovery" to emphasize the connection to and duality with the more well-studied problem of "truth discovery". To model items and their labels in a principled way, we draw upon Item Response Theory (IRT) which is the widely accepted theory behind standardized tests such as SAT and GRE. We start from an idealized setting where the relative performance of users is consistent across items and better users choose better fitting labels for each item. We posit that a principled algorithmic solution to our more general problem should solve this ideal setting correctly and observe that the response matrices in this setting obey the Consecutive Ones Property (C1P). While C1P is well understood algorithmically with various discrete algorithms, we devise a novel variant of the HITS algorithm which we call "HITSNDIFFS" (or HND), and prove that it can recover the ideal C1P-permutation in case it exists. Unlike fast combinatorial algorithms for finding the consecutive ones permutation (if it exists), HND also returns an ordering when such a permutation does not exist. Thus it provides a principled heuristic for our problem that is guaranteed to return the correct answer in the ideal setting. Our experiments show that HND produces user rankings with robustly high accuracy compared to state-of-the-art truth discovery methods. We also show that our novel variant of HITS scales better in the number of users than ABH, the only prior spectral C1P reconstruction algorithm.
Towards Unbiased Exploration in Partial Label Learning
Jul 02, 2023Abstract:We consider learning a probabilistic classifier from partially-labelled supervision (inputs denoted with multiple possibilities) using standard neural architectures with a softmax as the final layer. We identify a bias phenomenon that can arise from the softmax layer in even simple architectures that prevents proper exploration of alternative options, making the dynamics of gradient descent overly sensitive to initialisation. We introduce a novel loss function that allows for unbiased exploration within the space of alternative outputs. We give a theoretical justification for our loss function, and provide an extensive evaluation of its impact on synthetic data, on standard partially labelled benchmarks and on a contributed novel benchmark related to an existing rule learning challenge.
Factorized Graph Representations for Semi-Supervised Learning from Sparse Data
Mar 05, 2020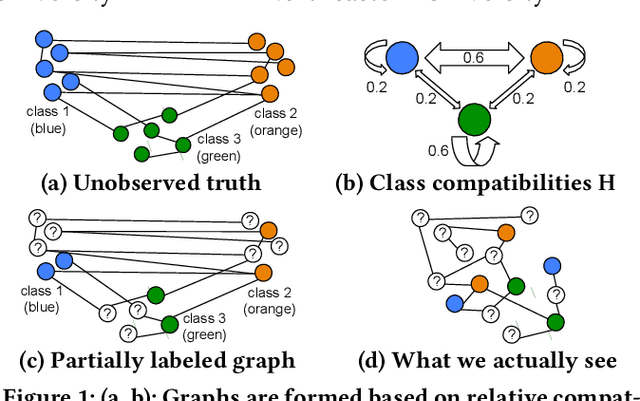
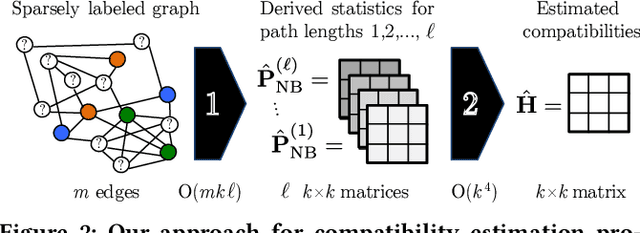
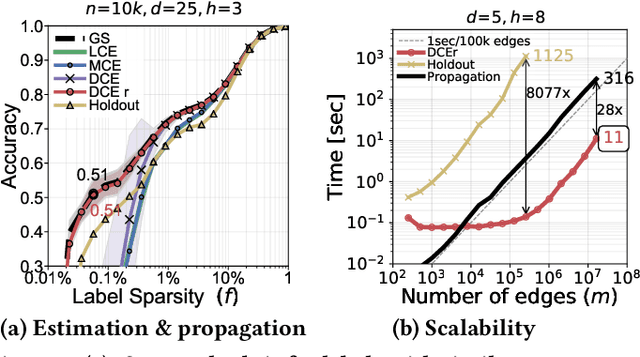
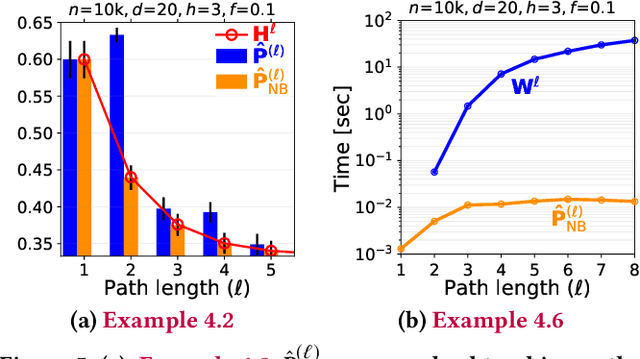
Abstract:Node classification is an important problem in graph data management. It is commonly solved by various label propagation methods that work iteratively starting from a few labeled seed nodes. For graphs with arbitrary compatibilities between classes, these methods crucially depend on knowing the compatibility matrix that must be provided by either domain experts or heuristics. Can we instead directly estimate the correct compatibilities from a sparsely labeled graph in a principled and scalable way? We answer this question affirmatively and suggest a method called distant compatibility estimation that works even on extremely sparsely labeled graphs (e.g., 1 in 10,000 nodes is labeled) in a fraction of the time it later takes to label the remaining nodes. Our approach first creates multiple factorized graph representations (with size independent of the graph) and then performs estimation on these smaller graph sketches. We define algebraic amplification as the more general idea of leveraging algebraic properties of an algorithm's update equations to amplify sparse signals. We show that our estimator is by orders of magnitude faster than an alternative approach and that the end-to-end classification accuracy is comparable to using gold standard compatibilities. This makes it a cheap preprocessing step for any existing label propagation method and removes the current dependence on heuristics.
Semi-Supervised Learning with Heterophily
Dec 28, 2016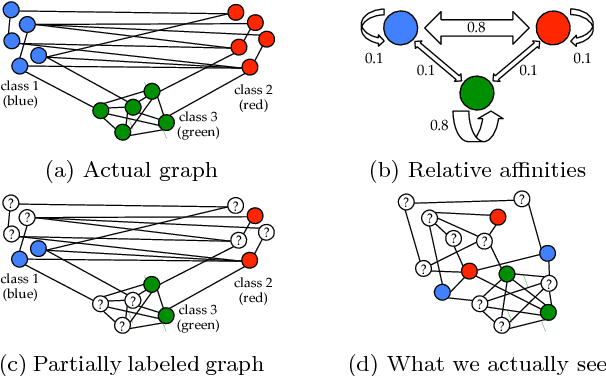
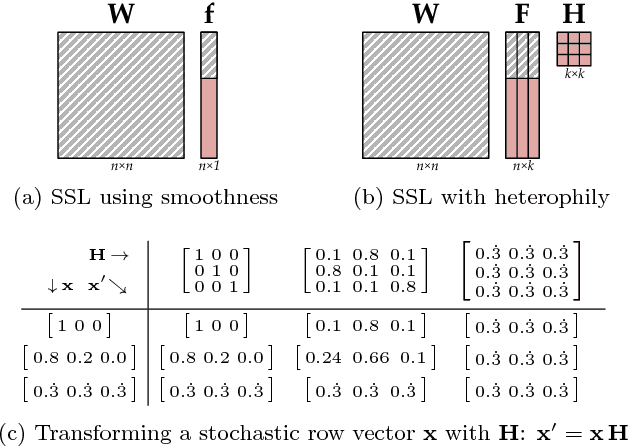

Abstract:We derive a family of linear inference algorithms that generalize existing graph-based label propagation algorithms by allowing them to propagate generalized assumptions about "attraction" or "compatibility" between classes of neighboring nodes (in particular those that involve heterophily between nodes where "opposites attract"). We thus call this formulation Semi-Supervised Learning with Heterophily (SSLH) and show how it generalizes and improves upon a recently proposed approach called Linearized Belief Propagation (LinBP). Importantly, our framework allows us to reduce the problem of estimating the relative compatibility between nodes from partially labeled graph to a simple optimization problem. The result is a very fast algorithm that -- despite its simplicity -- is surprisingly effective: we can classify unlabeled nodes within the same graph in the same time as LinBP but with a superior accuracy and despite our algorithm not knowing the compatibilities.
The Linearization of Belief Propagation on Pairwise Markov Networks
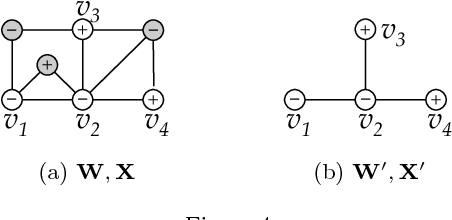
Dec 27, 2016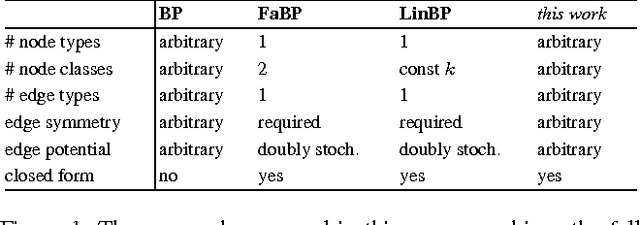
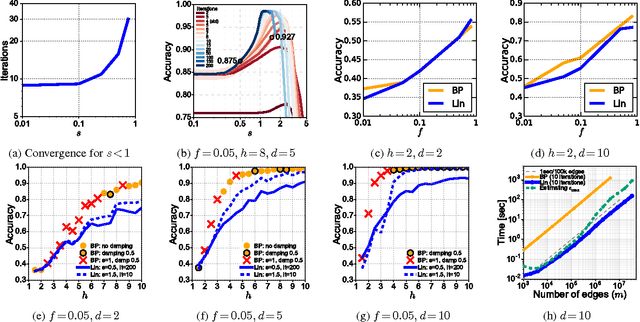

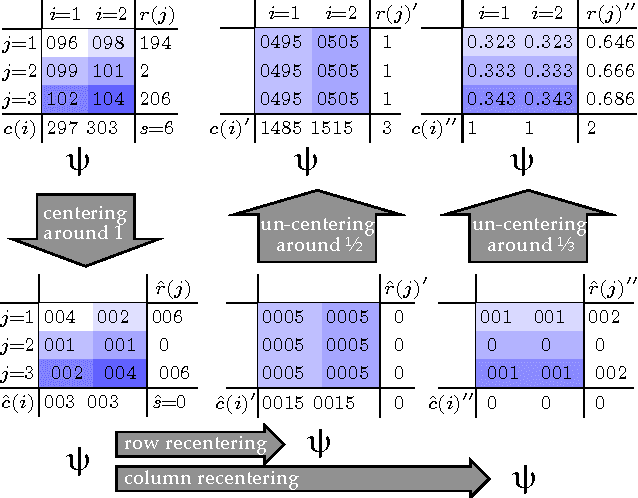
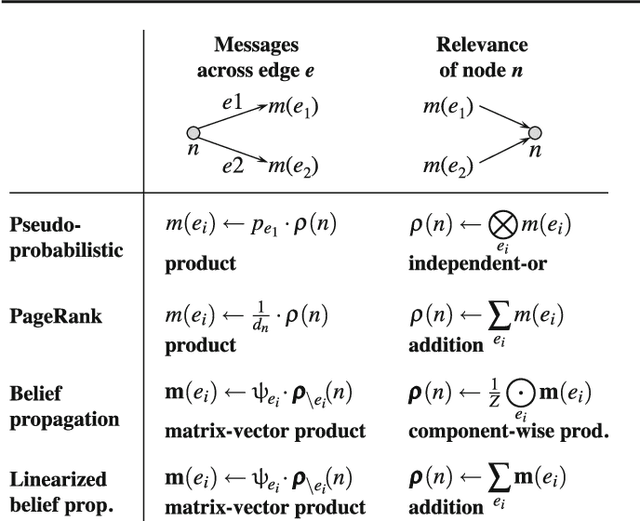
Abstract:Belief Propagation (BP) is a widely used approximation for exact probabilistic inference in graphical models, such as Markov Random Fields (MRFs). In graphs with cycles, however, no exact convergence guarantees for BP are known, in general. For the case when all edges in the MRF carry the same symmetric, doubly stochastic potential, recent works have proposed to approximate BP by linearizing the update equations around default values, which was shown to work well for the problem of node classification. The present paper generalizes all prior work and derives an approach that approximates loopy BP on any pairwise MRF with the problem of solving a linear equation system. This approach combines exact convergence guarantees and a fast matrix implementation with the ability to model heterogenous networks. Experiments on synthetic graphs with planted edge potentials show that the linearization has comparable labeling accuracy as BP for graphs with weak potentials, while speeding-up inference by orders of magnitude.
Dissociation and Propagation for Approximate Lifted Inference with Standard Relational Database Management Systems
Jun 14, 2016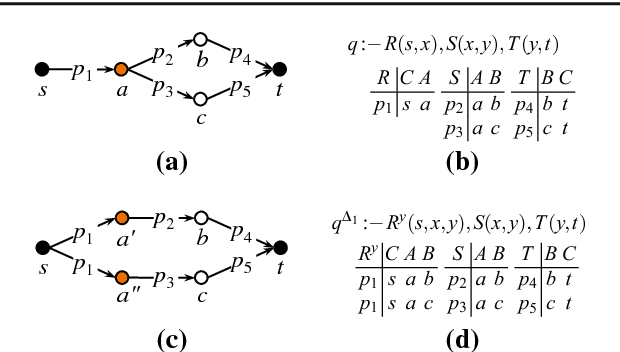

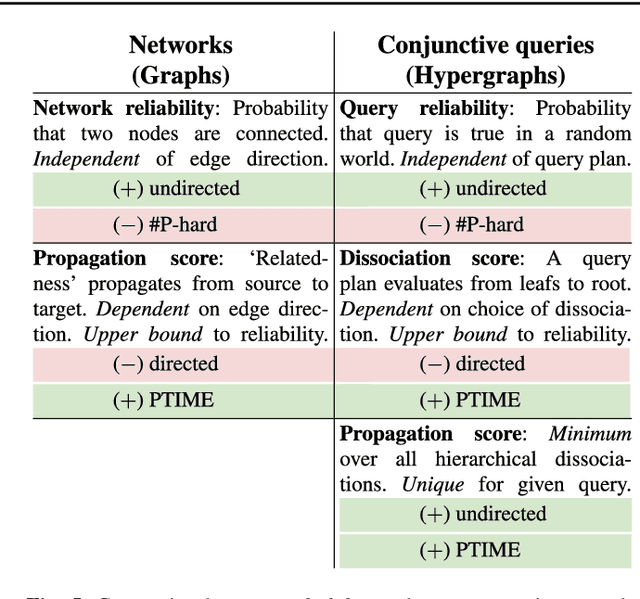
Abstract:Probabilistic inference over large data sets is a challenging data management problem since exact inference is generally #P-hard and is most often solved approximately with sampling-based methods today. This paper proposes an alternative approach for approximate evaluation of conjunctive queries with standard relational databases: In our approach, every query is evaluated entirely in the database engine by evaluating a fixed number of query plans, each providing an upper bound on the true probability, then taking their minimum. We provide an algorithm that takes into account important schema information to enumerate only the minimal necessary plans among all possible plans. Importantly, this algorithm is a strict generalization of all known PTIME self-join-free conjunctive queries: A query is in PTIME if and only if our algorithm returns one single plan. Furthermore, our approach is a generalization of a family of efficient ranking methods from graphs to hypergraphs. We also adapt three relational query optimization techniques to evaluate all necessary plans very fast. We give a detailed experimental evaluation of our approach and, in the process, provide a new way of thinking about the value of probabilistic methods over non-probabilistic methods for ranking query answers. We also note that the techniques developed in this paper apply immediately to lifted inference from statistical relational models since lifted inference corresponds to PTIME plans in probabilistic databases.
Approximate Lifted Inference with Probabilistic Databases
Dec 02, 2014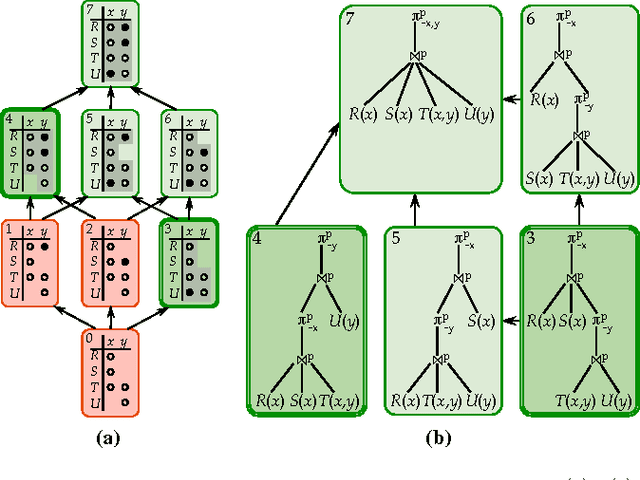
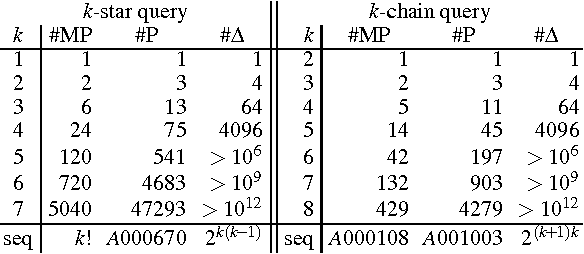

Abstract:This paper proposes a new approach for approximate evaluation of #P-hard queries with probabilistic databases. In our approach, every query is evaluated entirely in the database engine by evaluating a fixed number of query plans, each providing an upper bound on the true probability, then taking their minimum. We provide an algorithm that takes into account important schema information to enumerate only the minimal necessary plans among all possible plans. Importantly, this algorithm is a strict generalization of all known results of PTIME self-join-free conjunctive queries: A query is safe if and only if our algorithm returns one single plan. We also apply three relational query optimization techniques to evaluate all minimal safe plans very fast. We give a detailed experimental evaluation of our approach and, in the process, provide a new way of thinking about the value of probabilistic methods over non-probabilistic methods for ranking query answers.
Linearized and Single-Pass Belief Propagation
Oct 16, 2014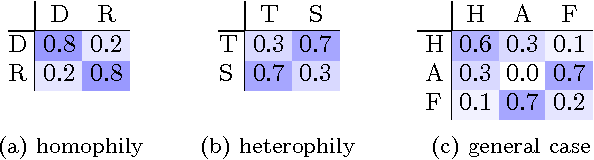
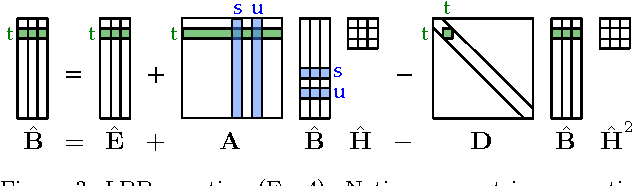
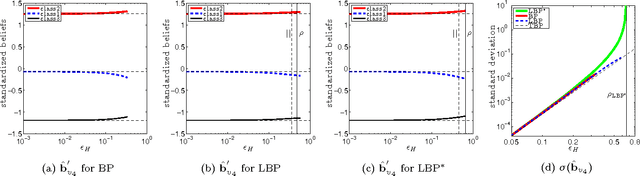
Abstract:How can we tell when accounts are fake or real in a social network? And how can we tell which accounts belong to liberal, conservative or centrist users? Often, we can answer such questions and label nodes in a network based on the labels of their neighbors and appropriate assumptions of homophily ("birds of a feather flock together") or heterophily ("opposites attract"). One of the most widely used methods for this kind of inference is Belief Propagation (BP) which iteratively propagates the information from a few nodes with explicit labels throughout a network until convergence. One main problem with BP, however, is that there are no known exact guarantees of convergence in graphs with loops. This paper introduces Linearized Belief Propagation (LinBP), a linearization of BP that allows a closed-form solution via intuitive matrix equations and, thus, comes with convergence guarantees. It handles homophily, heterophily, and more general cases that arise in multi-class settings. Plus, it allows a compact implementation in SQL. The paper also introduces Single-pass Belief Propagation (SBP), a "localized" version of LinBP that propagates information across every edge at most once and for which the final class assignments depend only on the nearest labeled neighbors. In addition, SBP allows fast incremental updates in dynamic networks. Our runtime experiments show that LinBP and SBP are orders of magnitude faster than standard
Oblivious Bounds on the Probability of Boolean Functions
Sep 21, 2014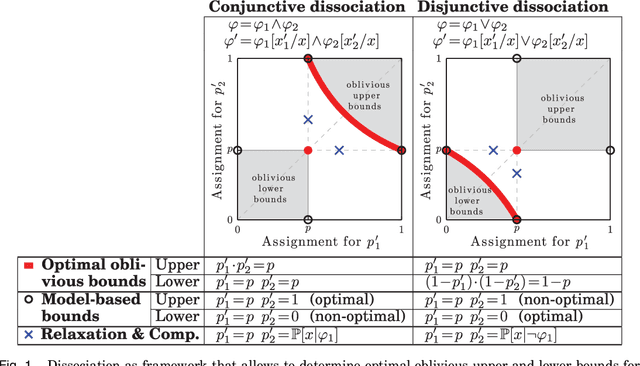
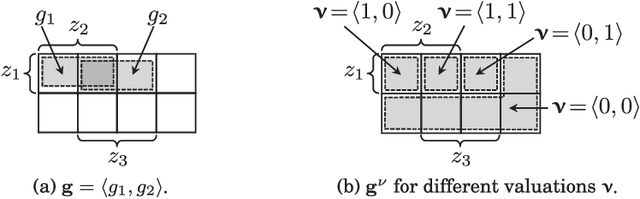
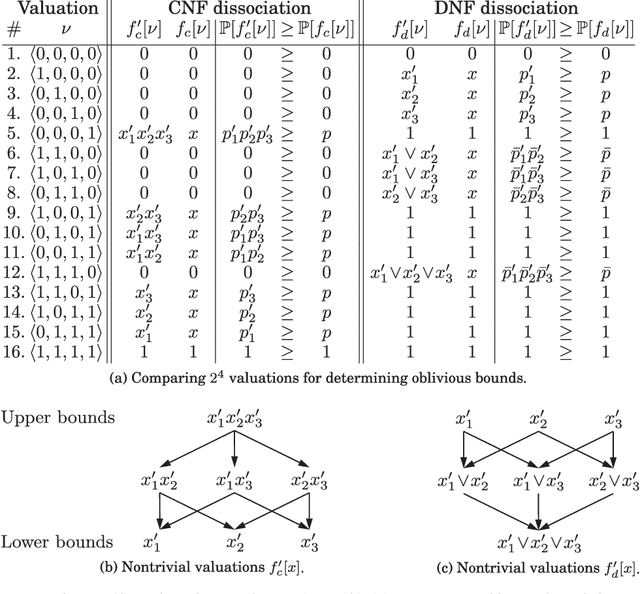
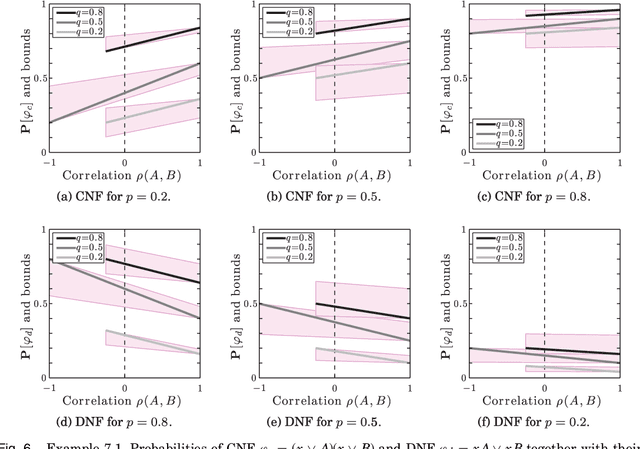
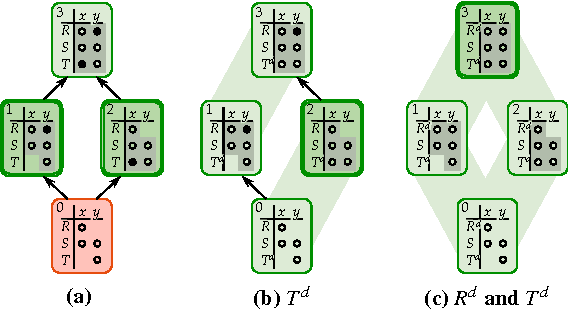
Abstract:This paper develops upper and lower bounds for the probability of Boolean functions by treating multiple occurrences of variables as independent and assigning them new individual probabilities. We call this approach dissociation and give an exact characterization of optimal oblivious bounds, i.e. when the new probabilities are chosen independent of the probabilities of all other variables. Our motivation comes from the weighted model counting problem (or, equivalently, the problem of computing the probability of a Boolean function), which is #P-hard in general. By performing several dissociations, one can transform a Boolean formula whose probability is difficult to compute, into one whose probability is easy to compute, and which is guaranteed to provide an upper or lower bound on the probability of the original formula by choosing appropriate probabilities for the dissociated variables. Our new bounds shed light on the connection between previous relaxation-based and model-based approximations and unify them as concrete choices in a larger design space. We also show how our theory allows a standard relational database management system (DBMS) to both upper and lower bound hard probabilistic queries in guaranteed polynomial time.
* 34 pages, 14 figures, supersedes: http://arxiv.org/abs/1105.2813
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge