Semi-Supervised Learning with Heterophily
Paper and Code
Dec 28, 2016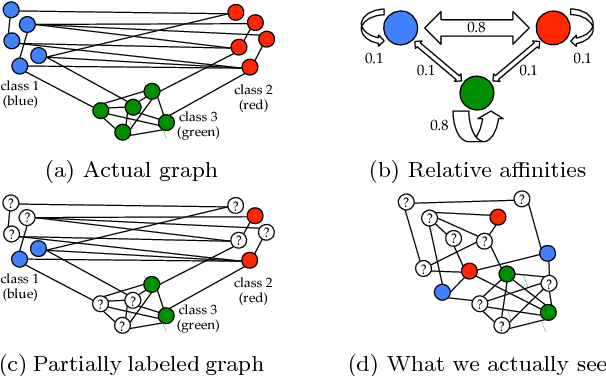
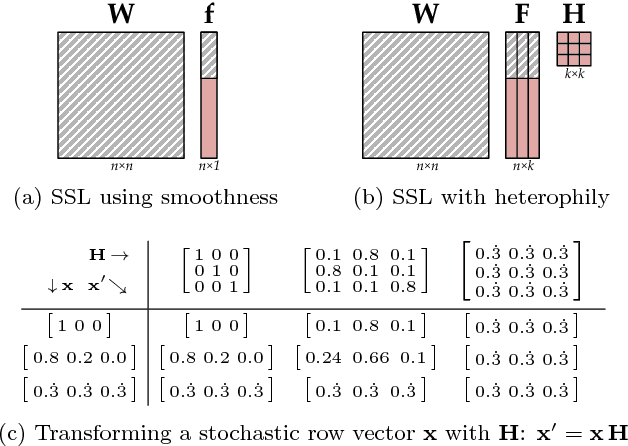

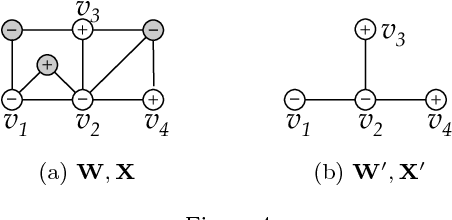
We derive a family of linear inference algorithms that generalize existing graph-based label propagation algorithms by allowing them to propagate generalized assumptions about "attraction" or "compatibility" between classes of neighboring nodes (in particular those that involve heterophily between nodes where "opposites attract"). We thus call this formulation Semi-Supervised Learning with Heterophily (SSLH) and show how it generalizes and improves upon a recently proposed approach called Linearized Belief Propagation (LinBP). Importantly, our framework allows us to reduce the problem of estimating the relative compatibility between nodes from partially labeled graph to a simple optimization problem. The result is a very fast algorithm that -- despite its simplicity -- is surprisingly effective: we can classify unlabeled nodes within the same graph in the same time as LinBP but with a superior accuracy and despite our algorithm not knowing the compatibilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge