Oblivious Bounds on the Probability of Boolean Functions
Paper and Code
Sep 21, 2014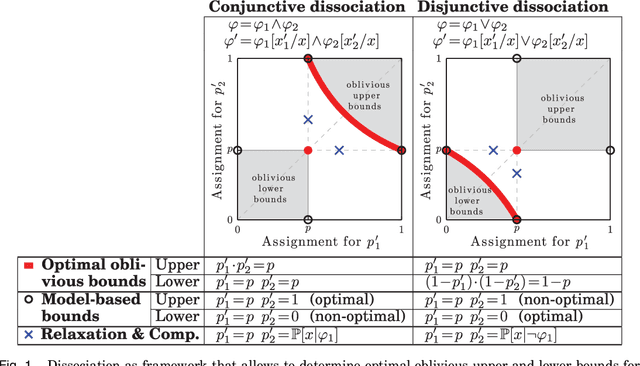
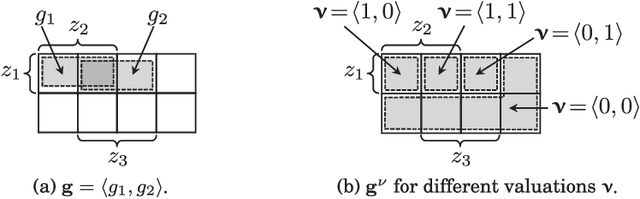
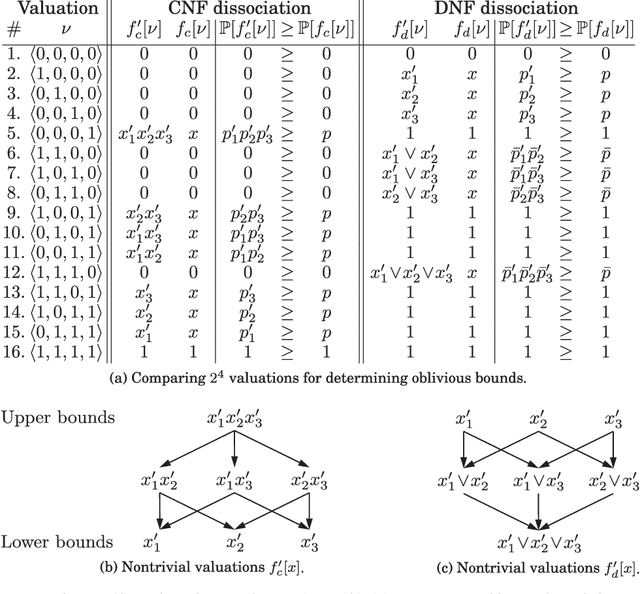
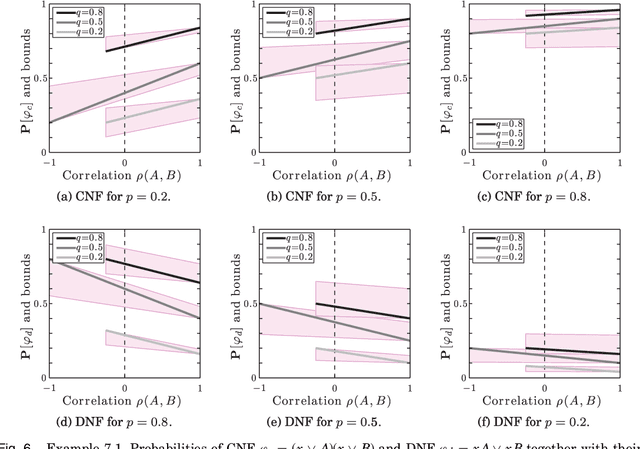
This paper develops upper and lower bounds for the probability of Boolean functions by treating multiple occurrences of variables as independent and assigning them new individual probabilities. We call this approach dissociation and give an exact characterization of optimal oblivious bounds, i.e. when the new probabilities are chosen independent of the probabilities of all other variables. Our motivation comes from the weighted model counting problem (or, equivalently, the problem of computing the probability of a Boolean function), which is #P-hard in general. By performing several dissociations, one can transform a Boolean formula whose probability is difficult to compute, into one whose probability is easy to compute, and which is guaranteed to provide an upper or lower bound on the probability of the original formula by choosing appropriate probabilities for the dissociated variables. Our new bounds shed light on the connection between previous relaxation-based and model-based approximations and unify them as concrete choices in a larger design space. We also show how our theory allows a standard relational database management system (DBMS) to both upper and lower bound hard probabilistic queries in guaranteed polynomial time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge