Proceedings of the second "international Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST'14)

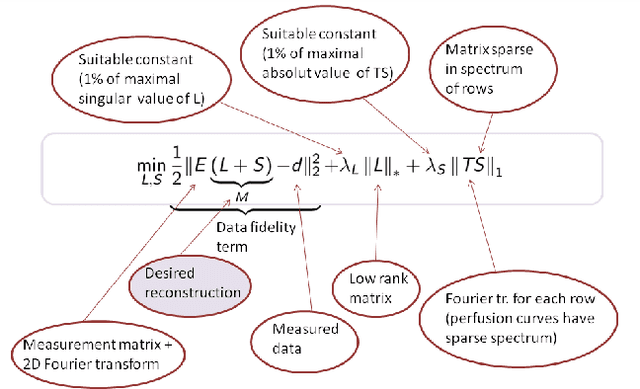
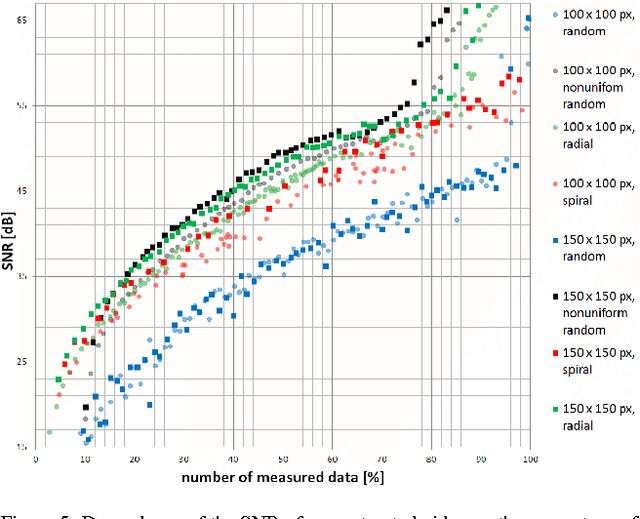
The implicit objective of the biennial "international - Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST) is to foster collaboration between international scientific teams by disseminating ideas through both specific oral/poster presentations and free discussions. For its second edition, the iTWIST workshop took place in the medieval and picturesque town of Namur in Belgium, from Wednesday August 27th till Friday August 29th, 2014. The workshop was conveniently located in "The Arsenal" building within walking distance of both hotels and town center. iTWIST'14 has gathered about 70 international participants and has featured 9 invited talks, 10 oral presentations, and 14 posters on the following themes, all related to the theory, application and generalization of the "sparsity paradigm": Sparsity-driven data sensing and processing; Union of low dimensional subspaces; Beyond linear and convex inverse problem; Matrix/manifold/graph sensing/processing; Blind inverse problems and dictionary learning; Sparsity and computational neuroscience; Information theory, geometry and randomness; Complexity/accuracy tradeoffs in numerical methods; Sparsity? What's next?; Sparse machine learning and inference.

Elastic-Net Regularization in Learning Theory

Within the framework of statistical learning theory we analyze in detail the so-called elastic-net regularization scheme proposed by Zou and Hastie for the selection of groups of correlated variables. To investigate on the statistical properties of this scheme and in particular on its consistency properties, we set up a suitable mathematical framework. Our setting is random-design regression where we allow the response variable to be vector-valued and we consider prediction functions which are linear combination of elements ({\em features}) in an infinite-dimensional dictionary. Under the assumption that the regression function admits a sparse representation on the dictionary, we prove that there exists a particular ``{\em elastic-net representation}'' of the regression function such that, if the number of data increases, the elastic-net estimator is consistent not only for prediction but also for variable/feature selection. Our results include finite-sample bounds and an adaptive scheme to select the regularization parameter. Moreover, using convex analysis tools, we derive an iterative thresholding algorithm for computing the elastic-net solution which is different from the optimization procedure originally proposed by Zou and Hastie