Sparse component separation from Poisson measurements

Blind source separation (BSS) aims at recovering signals from mixtures. This problem has been extensively studied in cases where the mixtures are contaminated with additive Gaussian noise. However, it is not well suited to describe data that are corrupted with Poisson measurements such as in low photon count optics or in high-energy astronomical imaging (e.g. observations from the Chandra or Fermi telescopes). To that purpose, we propose a novel BSS algorithm coined pGMCA that specifically tackles the blind separation of sparse sources from Poisson measurements.

Proceedings of the third "international Traveling Workshop on Interactions between Sparse models and Technology"

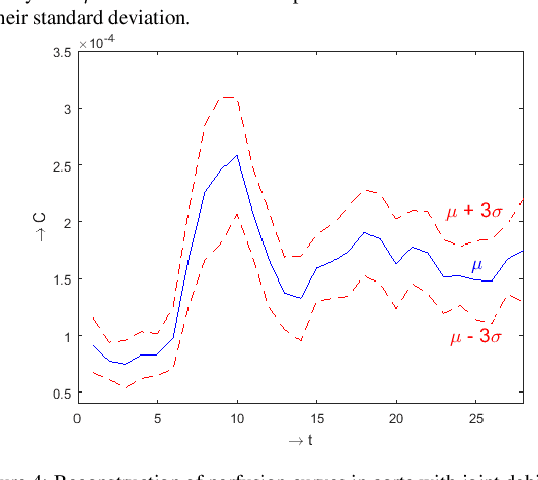
The third edition of the "international - Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST) took place in Aalborg, the 4th largest city in Denmark situated beautifully in the northern part of the country, from the 24th to 26th of August 2016. The workshop venue was at the Aalborg University campus. One implicit objective of this biennial workshop is to foster collaboration between international scientific teams by disseminating ideas through both specific oral/poster presentations and free discussions. For this third edition, iTWIST'16 gathered about 50 international participants and features 8 invited talks, 12 oral presentations, and 12 posters on the following themes, all related to the theory, application and generalization of the "sparsity paradigm": Sparsity-driven data sensing and processing (e.g., optics, computer vision, genomics, biomedical, digital communication, channel estimation, astronomy); Application of sparse models in non-convex/non-linear inverse problems (e.g., phase retrieval, blind deconvolution, self calibration); Approximate probabilistic inference for sparse problems; Sparse machine learning and inference; "Blind" inverse problems and dictionary learning; Optimization for sparse modelling; Information theory, geometry and randomness; Sparsity? What's next? (Discrete-valued signals; Union of low-dimensional spaces, Cosparsity, mixed/group norm, model-based, low-complexity models, ...); Matrix/manifold sensing/processing (graph, low-rank approximation, ...); Complexity/accuracy tradeoffs in numerical methods/optimization; Electronic/optical compressive sensors (hardware).