Proving Linear Mode Connectivity of Neural Networks via Optimal Transport

The energy landscape of high-dimensional non-convex optimization problems is crucial to understanding the effectiveness of modern deep neural network architectures. Recent works have experimentally shown that two different solutions found after two runs of a stochastic training are often connected by very simple continuous paths (e.g., linear) modulo a permutation of the weights. In this paper, we provide a framework theoretically explaining this empirical observation. Based on convergence rates in Wasserstein distance of empirical measures, we show that, with high probability, two wide enough two-layer neural networks trained with stochastic gradient descent are linearly connected. Additionally, we express upper and lower bounds on the width of each layer of two deep neural networks with independent neuron weights to be linearly connected. Finally, we empirically demonstrate the validity of our approach by showing how the dimension of the support of the weight distribution of neurons, which dictates Wasserstein convergence rates is correlated with linear mode connectivity.

PEPit: computer-assisted worst-case analyses of first-order optimization methods in Python

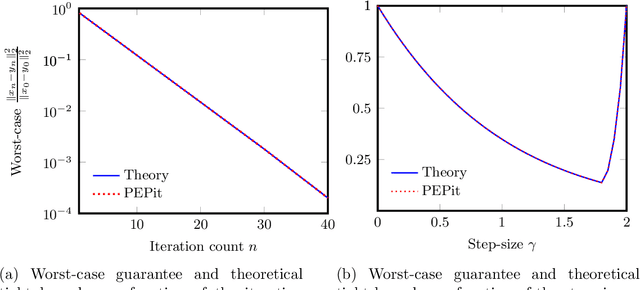
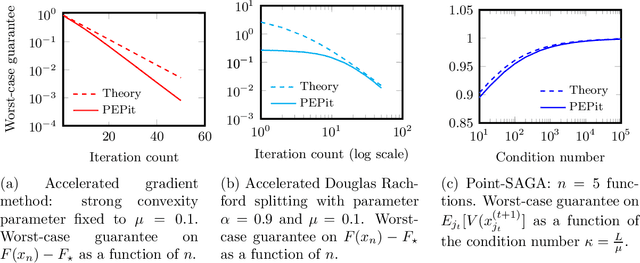
PEPit is a Python package aiming at simplifying the access to worst-case analyses of a large family of first-order optimization methods possibly involving gradient, projection, proximal, or linear optimization oracles, along with their approximate, or Bregman variants. In short, PEPit is a package enabling computer-assisted worst-case analyses of first-order optimization methods. The key underlying idea is to cast the problem of performing a worst-case analysis, often referred to as a performance estimation problem (PEP), as a semidefinite program (SDP) which can be solved numerically. For doing that, the package users are only required to write first-order methods nearly as they would have implemented them. The package then takes care of the SDP modelling parts, and the worst-case analysis is performed numerically via a standard solver.

A Study of Condition Numbers for First-Order Optimization

The study of first-order optimization algorithms (FOA) typically starts with assumptions on the objective functions, most commonly smoothness and strong convexity. These metrics are used to tune the hyperparameters of FOA. We introduce a class of perturbations quantified via a new norm, called *-norm. We show that adding a small perturbation to the objective function has an equivalently small impact on the behavior of any FOA, which suggests that it should have a minor impact on the tuning of the algorithm. However, we show that smoothness and strong convexity can be heavily impacted by arbitrarily small perturbations, leading to excessively conservative tunings and convergence issues. In view of these observations, we propose a notion of continuity of the metrics, which is essential for a robust tuning strategy. Since smoothness and strong convexity are not continuous, we propose a comprehensive study of existing alternative metrics which we prove to be continuous. We describe their mutual relations and provide their guaranteed convergence rates for the Gradient Descent algorithm accordingly tuned. Finally we discuss how our work impacts the theoretical understanding of FOA and their performances.

Online continual learning with no task boundaries

Continual learning is the ability of an agent to learn online with a non-stationary and never-ending stream of data. A key component for such never-ending learning process is to overcome the catastrophic forgetting of previously seen data, a problem that neural networks are well known to suffer from. The solutions developed so far often relax the problem of continual learning to the easier task-incremental setting, where the stream of data is divided into tasks with clear boundaries. In this paper, we break the limits and move to the more challenging online setting where we assume no information of tasks in the data stream. We start from the idea that each learning step should not increase the losses of the previously learned examples through constraining the optimization process. This means that the number of constraints grows linearly with the number of examples, which is a serious limitation. We develop a solution to select a fixed number of constraints that we use to approximate the feasible region defined by the original constraints. We compare our approach against the methods that rely on task boundaries to select a fixed set of examples, and show comparable or even better results, especially when the boundaries are blurry or when the data distributions are imbalanced.

Robust Detection of Covariate-Treatment Interactions in Clinical Trials

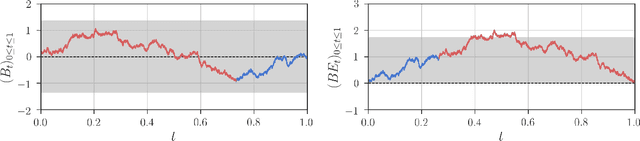
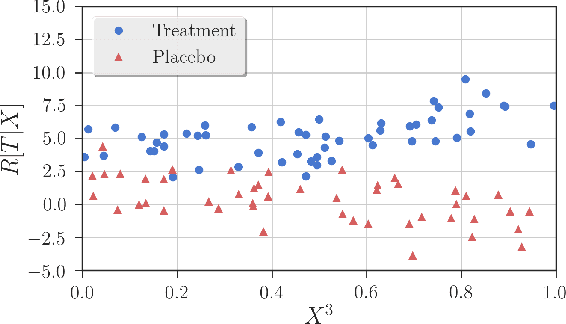
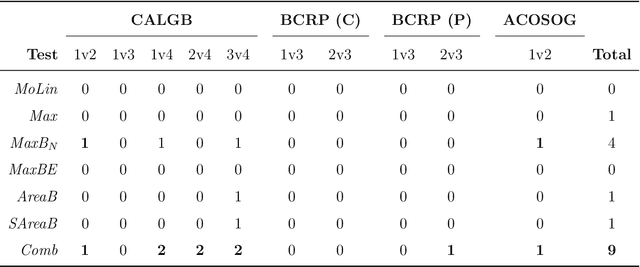
Detection of interactions between treatment effects and patient descriptors in clinical trials is critical for optimizing the drug development process. The increasing volume of data accumulated in clinical trials provides a unique opportunity to discover new biomarkers and further the goal of personalized medicine, but it also requires innovative robust biomarker detection methods capable of detecting non-linear, and sometimes weak, signals. We propose a set of novel univariate statistical tests, based on the theory of random walks, which are able to capture non-linear and non-monotonic covariate-treatment interactions. We also propose a novel combined test, which leverages the power of all of our proposed univariate tests into a single general-case tool. We present results for both synthetic trials as well as real-world clinical trials, where we compare our method with state-of-the-art techniques and demonstrate the utility and robustness of our approach.