Understanding Adam Requires Better Rotation Dependent Assumptions

Despite its widespread adoption, Adam's advantage over Stochastic Gradient Descent (SGD) lacks a comprehensive theoretical explanation. This paper investigates Adam's sensitivity to rotations of the parameter space. We demonstrate that Adam's performance in training transformers degrades under random rotations of the parameter space, indicating a crucial sensitivity to the choice of basis. This reveals that conventional rotation-invariant assumptions are insufficient to capture Adam's advantages theoretically. To better understand the rotation-dependent properties that benefit Adam, we also identify structured rotations that preserve or even enhance its empirical performance. We then examine the rotation-dependent assumptions in the literature, evaluating their adequacy in explaining Adam's behavior across various rotation types. This work highlights the need for new, rotation-dependent theoretical frameworks to fully understand Adam's empirical success in modern machine learning tasks.

From Conformal Predictions to Confidence Regions

Conformal prediction methodologies have significantly advanced the quantification of uncertainties in predictive models. Yet, the construction of confidence regions for model parameters presents a notable challenge, often necessitating stringent assumptions regarding data distribution or merely providing asymptotic guarantees. We introduce a novel approach termed CCR, which employs a combination of conformal prediction intervals for the model outputs to establish confidence regions for model parameters. We present coverage guarantees under minimal assumptions on noise and that is valid in finite sample regime. Our approach is applicable to both split conformal predictions and black-box methodologies including full or cross-conformal approaches. In the specific case of linear models, the derived confidence region manifests as the feasible set of a Mixed-Integer Linear Program (MILP), facilitating the deduction of confidence intervals for individual parameters and enabling robust optimization. We empirically compare CCR to recent advancements in challenging settings such as with heteroskedastic and non-Gaussian noise.

Finite Sample Confidence Regions for Linear Regression Parameters Using Arbitrary Predictors

We explore a novel methodology for constructing confidence regions for parameters of linear models, using predictions from any arbitrary predictor. Our framework requires minimal assumptions on the noise and can be extended to functions deviating from strict linearity up to some adjustable threshold, thereby accommodating a comprehensive and pragmatically relevant set of functions. The derived confidence regions can be cast as constraints within a Mixed Integer Linear Programming framework, enabling optimisation of linear objectives. This representation enables robust optimization and the extraction of confidence intervals for specific parameter coordinates. Unlike previous methods, the confidence region can be empty, which can be used for hypothesis testing. Finally, we validate the empirical applicability of our method on synthetic data.

Expecting The Unexpected: Towards Broad Out-Of-Distribution Detection

Improving the reliability of deployed machine learning systems often involves developing methods to detect out-of-distribution (OOD) inputs. However, existing research often narrowly focuses on samples from classes that are absent from the training set, neglecting other types of plausible distribution shifts. This limitation reduces the applicability of these methods in real-world scenarios, where systems encounter a wide variety of anomalous inputs. In this study, we categorize five distinct types of distribution shifts and critically evaluate the performance of recent OOD detection methods on each of them. We publicly release our benchmark under the name BROAD (Benchmarking Resilience Over Anomaly Diversity). Our findings reveal that while these methods excel in detecting unknown classes, their performance is inconsistent when encountering other types of distribution shifts. In other words, they only reliably detect unexpected inputs that they have been specifically designed to expect. As a first step toward broad OOD detection, we learn a generative model of existing detection scores with a Gaussian mixture. By doing so, we present an ensemble approach that offers a more consistent and comprehensive solution for broad OOD detection, demonstrating superior performance compared to existing methods. Our code to download BROAD and reproduce our experiments is publicly available.

No Wrong Turns: The Simple Geometry Of Neural Networks Optimization Paths

Understanding the optimization dynamics of neural networks is necessary for closing the gap between theory and practice. Stochastic first-order optimization algorithms are known to efficiently locate favorable minima in deep neural networks. This efficiency, however, contrasts with the non-convex and seemingly complex structure of neural loss landscapes. In this study, we delve into the fundamental geometric properties of sampled gradients along optimization paths. We focus on two key quantities, which appear in the restricted secant inequality and error bound. Both hold high significance for first-order optimization. Our analysis reveals that these quantities exhibit predictable, consistent behavior throughout training, despite the stochasticity induced by sampling minibatches. Our findings suggest that not only do optimization trajectories never encounter significant obstacles, but they also maintain stable dynamics during the majority of training. These observed properties are sufficiently expressive to theoretically guarantee linear convergence and prescribe learning rate schedules mirroring empirical practices. We conduct our experiments on image classification, semantic segmentation and language modeling across different batch sizes, network architectures, datasets, optimizers, and initialization seeds. We discuss the impact of each factor. Our work provides novel insights into the properties of neural network loss functions, and opens the door to theoretical frameworks more relevant to prevalent practice.

Towards Out-of-Distribution Adversarial Robustness

Adversarial robustness continues to be a major challenge for deep learning. A core issue is that robustness to one type of attack often fails to transfer to other attacks. While prior work establishes a theoretical trade-off in robustness against different $L_p$ norms, we show that there is potential for improvement against many commonly used attacks by adopting a domain generalisation approach. Concretely, we treat each type of attack as a domain, and apply the Risk Extrapolation method (REx), which promotes similar levels of robustness against all training attacks. Compared to existing methods, we obtain similar or superior worst-case adversarial robustness on attacks seen during training. Moreover, we achieve superior performance on families or tunings of attacks only encountered at test time. On ensembles of attacks, our approach improves the accuracy from 3.4% the best existing baseline to 25.9% on MNIST, and from 16.9% to 23.5% on CIFAR10.

CADet: Fully Self-Supervised Anomaly Detection With Contrastive Learning

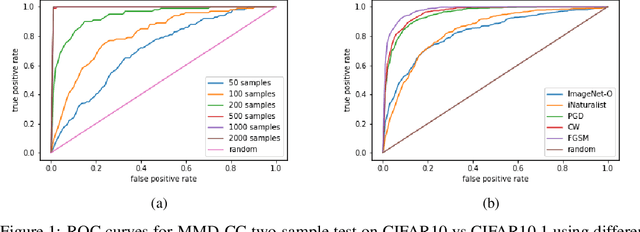
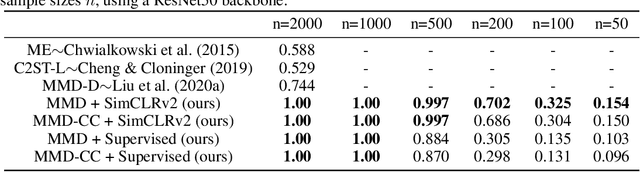
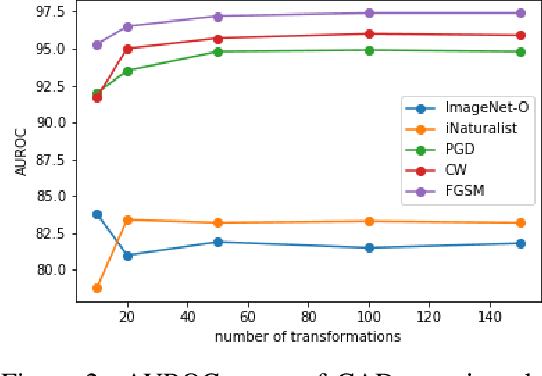
Handling out-of-distribution (OOD) samples has become a major stake in the real-world deployment of machine learning systems. This work explores the application of self-supervised contrastive learning to the simultaneous detection of two types of OOD samples: unseen classes and adversarial perturbations. Since in practice the distribution of such samples is not known in advance, we do not assume access to OOD examples. We show that similarity functions trained with contrastive learning can be leveraged with the maximum mean discrepancy (MMD) two-sample test to verify whether two independent sets of samples are drawn from the same distribution. Inspired by this approach, we introduce CADet (Contrastive Anomaly Detection), a method based on image augmentations to perform anomaly detection on single samples. CADet compares favorably to adversarial detection methods to detect adversarially perturbed samples on ImageNet. Simultaneously, it achieves comparable performance to unseen label detection methods on two challenging benchmarks: ImageNet-O and iNaturalist. CADet is fully self-supervised and requires neither labels for in-distribution samples nor access to OOD examples.

A Study of Condition Numbers for First-Order Optimization

The study of first-order optimization algorithms (FOA) typically starts with assumptions on the objective functions, most commonly smoothness and strong convexity. These metrics are used to tune the hyperparameters of FOA. We introduce a class of perturbations quantified via a new norm, called *-norm. We show that adding a small perturbation to the objective function has an equivalently small impact on the behavior of any FOA, which suggests that it should have a minor impact on the tuning of the algorithm. However, we show that smoothness and strong convexity can be heavily impacted by arbitrarily small perturbations, leading to excessively conservative tunings and convergence issues. In view of these observations, we propose a notion of continuity of the metrics, which is essential for a robust tuning strategy. Since smoothness and strong convexity are not continuous, we propose a comprehensive study of existing alternative metrics which we prove to be continuous. We describe their mutual relations and provide their guaranteed convergence rates for the Gradient Descent algorithm accordingly tuned. Finally we discuss how our work impacts the theoretical understanding of FOA and their performances.