What do near-optimal learning rate schedules look like?

A basic unanswered question in neural network training is: what is the best learning rate schedule shape for a given workload? The choice of learning rate schedule is a key factor in the success or failure of the training process, but beyond having some kind of warmup and decay, there is no consensus on what makes a good schedule shape. To answer this question, we designed a search procedure to find the best shapes within a parameterized schedule family. Our approach factors out the schedule shape from the base learning rate, which otherwise would dominate cross-schedule comparisons. We applied our search procedure to a variety of schedule families on three workloads: linear regression, image classification on CIFAR-10, and small-scale language modeling on Wikitext103. We showed that our search procedure indeed generally found near-optimal schedules. We found that warmup and decay are robust features of good schedules, and that commonly used schedule families are not optimal on these workloads. Finally, we explored how the outputs of our shape search depend on other optimization hyperparameters, and found that weight decay can have a strong effect on the optimal schedule shape. To the best of our knowledge, our results represent the most comprehensive results on near-optimal schedule shapes for deep neural network training, to date.

Takeuchi's Information Criteria as Generalization Measures for DNNs Close to NTK Regime

Generalization measures have been studied extensively in the machine learning community to better characterize generalization gaps. However, establishing a reliable generalization measure for statistically singular models such as deep neural networks (DNNs) is difficult due to their complex nature. This study focuses on Takeuchi's information criterion (TIC) to investigate the conditions under which this classical measure can effectively explain the generalization gaps of DNNs. Importantly, the developed theory indicates the applicability of TIC near the neural tangent kernel (NTK) regime. In a series of experiments, we trained more than 5,000 DNN models with 12 architectures, including large models (e.g., VGG-16), on four datasets, and estimated the corresponding TIC values to examine the relationship between the generalization gap and the TIC estimates. We applied several TIC approximation methods with feasible computational costs and assessed the accuracy trade-off. Our experimental results indicate that the estimated TIC values correlate well with the generalization gap under conditions close to the NTK regime. However, we show both theoretically and empirically that outside the NTK regime such correlation disappears. Finally, we demonstrate that TIC provides better trial pruning ability than existing methods for hyperparameter optimization.

Adaptive Batch Sizes Using Non-Euclidean Gradient Noise Scales for Stochastic Sign and Spectral Descent

To maximize hardware utilization, modern machine learning systems typically employ large constant or manually tuned batch size schedules, relying on heuristics that are brittle and costly to tune. Existing adaptive strategies based on gradient noise scale (GNS) offer a principled alternative. However, their assumption of SGD's Euclidean geometry creates a fundamental mismatch with popular optimizers based on generalized norms, such as signSGD / Signum ($\ell_\infty$) and stochastic spectral descent (specSGD) / Muon ($\mathcal{S}_\infty$). In this work, we derive gradient noise scales for signSGD and specSGD that naturally emerge from the geometry of their respective dual norms. To practically estimate these non-Euclidean metrics, we propose an efficient variance estimation procedure that leverages the local mini-batch gradients on different ranks in distributed data-parallel systems. Our experiments demonstrate that adaptive batch size strategies using non-Euclidean GNS enable us to match the validation loss of constant-batch baselines while reducing training steps by up to 66% for Signum and Muon on a 160 million parameter Llama model.

Revisiting Generalization Measures Beyond IID: An Empirical Study under Distributional Shift

Generalization remains a central yet unresolved challenge in deep learning, particularly the ability to predict a model's performance beyond its training distribution using quantities available prior to test-time evaluation. Building on the large-scale study of Jiang et al. (2020). and concerns by Dziugaite et al. (2020). about instability across training configurations, we benchmark the robustness of generalization measures beyond IID regime. We train small-to-medium models over 10,000 hyperparameter configurations and evaluate more than 40 measures computable from the trained model and the available training data alone. We significantly broaden the experimental scope along multiple axes: (i) extending the evaluation beyond the standard IID setting to include benchmarking for robustness across diverse distribution shifts, (ii) evaluating multiple architectures and training recipes, and (iii) newly incorporating calibration- and information-criteria-based measures to assess their alignment with both IID and OOD generalization. We find that distribution shifts can substantially alter the predictive performance of many generalization measures, while a smaller subset remains comparatively stable across settings.

Analysis of Muon's Convergence and Critical Batch Size

This paper presents a theoretical analysis of Muon, a new optimizer that leverages the inherent matrix structure of neural network parameters. We provide convergence proofs for four practical variants of Muon: with and without Nesterov momentum, and with and without weight decay. We then show that adding weight decay leads to strictly tighter bounds on both the parameter and gradient norms, and we clarify the relationship between the weight decay coefficient and the learning rate. Finally, we derive Muon's critical batch size minimizing the stochastic first-order oracle (SFO) complexity, which is the stochastic computational cost, and validate our theoretical findings with experiments.

On Fairness of Task Arithmetic: The Role of Task Vectors

Model editing techniques, particularly task arithmetic using task vectors, have shown promise in efficiently modifying pre-trained models through arithmetic operations like task addition and negation. Despite computational advantages, these methods may inadvertently affect model fairness, creating risks in sensitive applications like hate speech detection. However, the fairness implications of task arithmetic remain largely unexplored, presenting a critical gap in the existing literature. We systematically examine how manipulating task vectors affects fairness metrics, including Demographic Parity and Equalized Odds. To rigorously assess these effects, we benchmark task arithmetic against full fine-tuning, a costly but widely used baseline, and Low-Rank Adaptation (LoRA), a prevalent parameter-efficient fine-tuning method. Additionally, we explore merging task vectors from models fine-tuned on demographic subgroups vulnerable to hate speech, investigating whether fairness outcomes can be controlled by adjusting task vector coefficients, potentially enabling tailored model behavior. Our results offer novel insights into the fairness implications of model editing and establish a foundation for fairness-aware and responsible model editing practices.

Pseudo-Asynchronous Local SGD: Robust and Efficient Data-Parallel Training

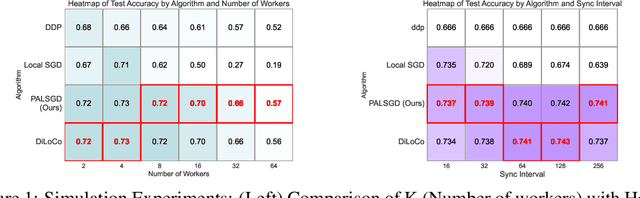
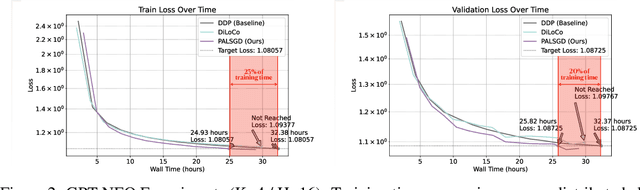
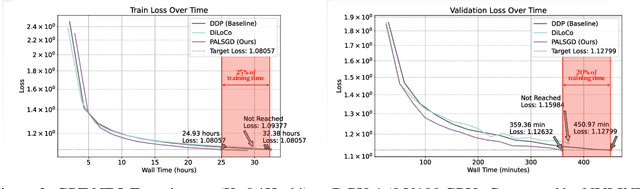
Following AI scaling trends, frontier models continue to grow in size and continue to be trained on larger datasets. Training these models requires huge investments in exascale computational resources, which has in turn driven development of distributed deep learning methods. Data parallelism is an essential approach to speed up training, but it requires frequent global communication between workers, which can bottleneck training at the largest scales. In this work, we propose a method called Pseudo-Asynchronous Local SGD (PALSGD) to improve the efficiency of data-parallel training. PALSGD is an extension of Local SGD (Stich, 2018) and DiLoCo (Douillard et al., 2023), designed to further reduce communication frequency by introducing a pseudo-synchronization mechanism. PALSGD allows the use of longer synchronization intervals compared to standard Local SGD. Despite the reduced communication frequency, the pseudo-synchronization approach ensures that model consistency is maintained, leading to performance results comparable to those achieved with more frequent synchronization. Furthermore, we provide a theoretical analysis of PALSGD, establishing its convergence and deriving its convergence rate. This analysis offers insights into the algorithm's behavior and performance guarantees. We evaluated PALSGD on image classification and language modeling tasks. Our results show that PALSGD achieves better performance in less time compared to existing methods like Distributed Data Parallel (DDP), and DiLoCo. Notably, PALSGD trains 18.4% faster than DDP on ImageNet-1K with ResNet-50, 24.4% faster than DDP on TinyStories with GPT-Neo125M, and 21.1% faster than DDP on TinyStories with GPT-Neo-8M.

Geometric Insights into Focal Loss: Reducing Curvature for Enhanced Model Calibration

The key factor in implementing machine learning algorithms in decision-making situations is not only the accuracy of the model but also its confidence level. The confidence level of a model in a classification problem is often given by the output vector of a softmax function for convenience. However, these values are known to deviate significantly from the actual expected model confidence. This problem is called model calibration and has been studied extensively. One of the simplest techniques to tackle this task is focal loss, a generalization of cross-entropy by introducing one positive parameter. Although many related studies exist because of the simplicity of the idea and its formalization, the theoretical analysis of its behavior is still insufficient. In this study, our objective is to understand the behavior of focal loss by reinterpreting this function geometrically. Our analysis suggests that focal loss reduces the curvature of the loss surface in training the model. This indicates that curvature may be one of the essential factors in achieving model calibration. We design numerical experiments to support this conjecture to reveal the behavior of focal loss and the relationship between calibration performance and curvature.

Augmenting NER Datasets with LLMs: Towards Automated and Refined Annotation

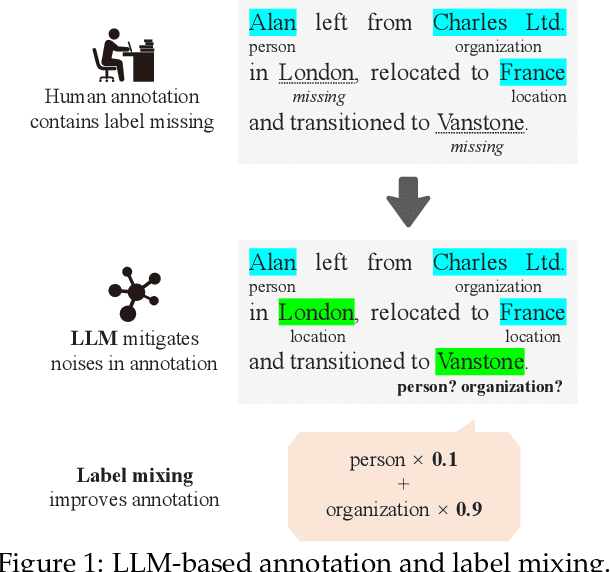
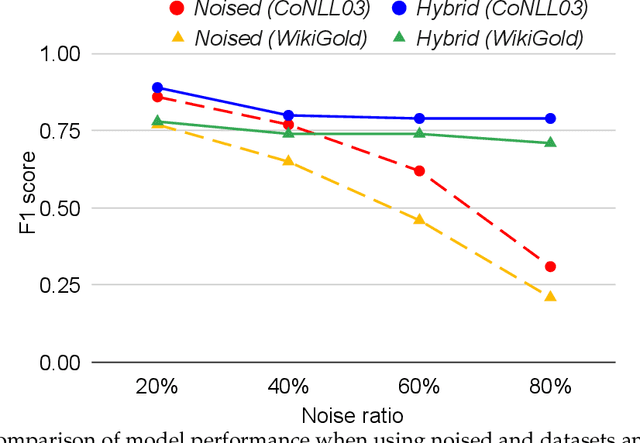
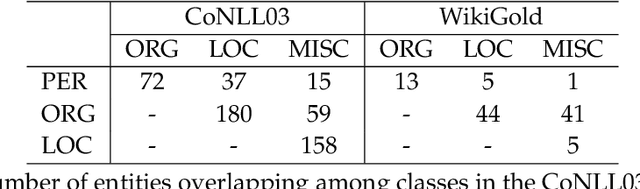
In the field of Natural Language Processing (NLP), Named Entity Recognition (NER) is recognized as a critical technology, employed across a wide array of applications. Traditional methodologies for annotating datasets for NER models are challenged by high costs and variations in dataset quality. This research introduces a novel hybrid annotation approach that synergizes human effort with the capabilities of Large Language Models (LLMs). This approach not only aims to ameliorate the noise inherent in manual annotations, such as omissions, thereby enhancing the performance of NER models, but also achieves this in a cost-effective manner. Additionally, by employing a label mixing strategy, it addresses the issue of class imbalance encountered in LLM-based annotations. Through an analysis across multiple datasets, this method has been consistently shown to provide superior performance compared to traditional annotation methods, even under constrained budget conditions. This study illuminates the potential of leveraging LLMs to improve dataset quality, introduces a novel technique to mitigate class imbalances, and demonstrates the feasibility of achieving high-performance NER in a cost-effective way.

Towards Understanding Variants of Invariant Risk Minimization through the Lens of Calibration

Machine learning models traditionally assume that training and test data are independently and identically distributed. However, in real-world applications, the test distribution often differs from training. This problem, known as out-of-distribution generalization, challenges conventional models. Invariant Risk Minimization (IRM) emerges as a solution, aiming to identify features invariant across different environments to enhance out-of-distribution robustness. However, IRM's complexity, particularly its bi-level optimization, has led to the development of various approximate methods. Our study investigates these approximate IRM techniques, employing the Expected Calibration Error (ECE) as a key metric. ECE, which measures the reliability of model prediction, serves as an indicator of whether models effectively capture environment-invariant features. Through a comparative analysis of datasets with distributional shifts, we observe that Information Bottleneck-based IRM, which condenses representational information, achieves a balance in improving ECE while preserving accuracy relatively. This finding is pivotal, as it demonstrates a feasible path to maintaining robustness without compromising accuracy. Nonetheless, our experiments also caution against over-regularization, which can diminish accuracy. This underscores the necessity for a systematic approach in evaluating out-of-distribution generalization metrics, one that beyond mere accuracy to address the nuanced interplay between accuracy and calibration.