Optimal Growth Schedules for Batch Size and Learning Rate in SGD that Reduce SFO Complexity

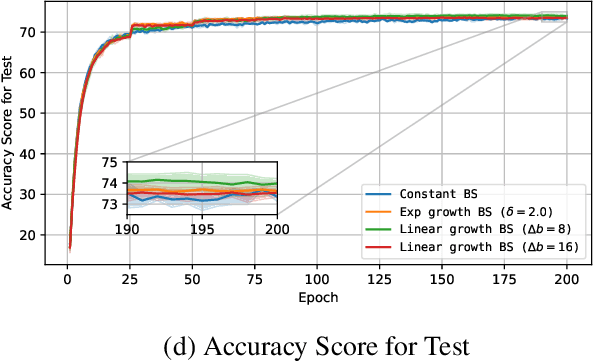
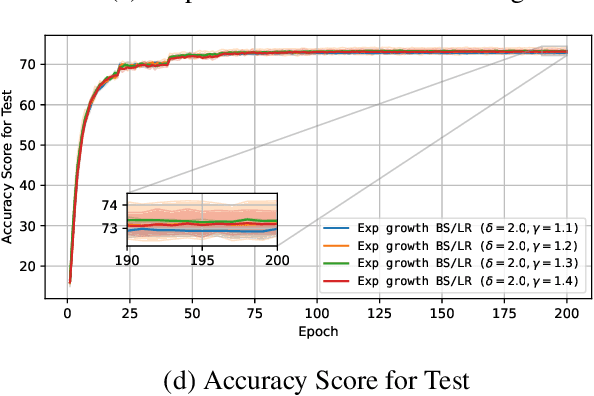
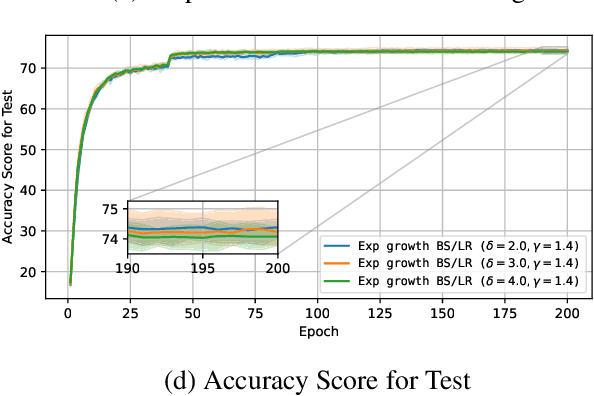
The unprecedented growth of deep learning models has enabled remarkable advances but introduced substantial computational bottlenecks. A key factor contributing to training efficiency is batch-size and learning-rate scheduling in stochastic gradient methods. However, naive scheduling of these hyperparameters can degrade optimization efficiency and compromise generalization. Motivated by recent theoretical insights, we investigated how the batch size and learning rate should be increased during training to balance efficiency and convergence. We analyzed this problem on the basis of stochastic first-order oracle (SFO) complexity, defined as the expected number of gradient evaluations needed to reach an $\epsilon$-approximate stationary point of the empirical loss. We theoretically derived optimal growth schedules for the batch size and learning rate that reduce SFO complexity and validated them through extensive experiments. Our results offer both theoretical insights and practical guidelines for scalable and efficient large-batch training in deep learning.

Adaptive Batch Size and Learning Rate Scheduler for Stochastic Gradient Descent Based on Minimization of Stochastic First-order Oracle Complexity

The convergence behavior of mini-batch stochastic gradient descent (SGD) is highly sensitive to the batch size and learning rate settings. Recent theoretical studies have identified the existence of a critical batch size that minimizes stochastic first-order oracle (SFO) complexity, defined as the expected number of gradient evaluations required to reach a stationary point of the empirical loss function in a deep neural network. An adaptive scheduling strategy is introduced to accelerate SGD that leverages theoretical findings on the critical batch size. The batch size and learning rate are adjusted on the basis of the observed decay in the full gradient norm during training. Experiments using an adaptive joint scheduler based on this strategy demonstrated improved convergence speed compared with that of existing schedulers.

Analysis of Muon's Convergence and Critical Batch Size

This paper presents a theoretical analysis of Muon, a new optimizer that leverages the inherent matrix structure of neural network parameters. We provide convergence proofs for four practical variants of Muon: with and without Nesterov momentum, and with and without weight decay. We then show that adding weight decay leads to strictly tighter bounds on both the parameter and gradient norms, and we clarify the relationship between the weight decay coefficient and the learning rate. Finally, we derive Muon's critical batch size minimizing the stochastic first-order oracle (SFO) complexity, which is the stochastic computational cost, and validate our theoretical findings with experiments.

Faster Convergence of Riemannian Stochastic Gradient Descent with Increasing Batch Size

Many models used in machine learning have become so large that even computer computation of the full gradient of the loss function is impractical. This has made it necessary to efficiently train models using limited available information, such as batch size and learning rate. We have theoretically analyzed the use of Riemannian stochastic gradient descent (RSGD) and found that using an increasing batch size leads to faster RSGD convergence than using a constant batch size not only with a constant learning rate but also with a decaying learning rate, such as cosine annealing decay and polynomial decay. In particular, RSGD has a better convergence rate $O(\frac{1}{\sqrt{T}})$ than the existing rate $O(\frac{\sqrt{\log T}}{\sqrt[4]{T}})$ with a diminishing learning rate, where $T$ is the number of iterations. The results of experiments on principal component analysis and low-rank matrix completion problems confirmed that, except for the MovieLens dataset and a constant learning rate, using a polynomial growth batch size or an exponential growth batch size results in better performance than using a constant batch size.

Increasing Batch Size Improves Convergence of Stochastic Gradient Descent with Momentum

Stochastic gradient descent with momentum (SGDM), which is defined by adding a momentum term to SGD, has been well studied in both theory and practice. Theoretically investigated results showed that the settings of the learning rate and momentum weight affect the convergence of SGDM. Meanwhile, practical results showed that the setting of batch size strongly depends on the performance of SGDM. In this paper, we focus on mini-batch SGDM with constant learning rate and constant momentum weight, which is frequently used to train deep neural networks in practice. The contribution of this paper is showing theoretically that using a constant batch size does not always minimize the expectation of the full gradient norm of the empirical loss in training a deep neural network, whereas using an increasing batch size definitely minimizes it, that is, increasing batch size improves convergence of mini-batch SGDM. We also provide numerical results supporting our analyses, indicating specifically that mini-batch SGDM with an increasing batch size converges to stationary points faster than with a constant batch size. Python implementations of the optimizers used in the numerical experiments are available at https://anonymous.4open.science/r/momentum-increasing-batch-size-888C/.

Explicit and Implicit Graduated Optimization in Deep Neural Networks

Graduated optimization is a global optimization technique that is used to minimize a multimodal nonconvex function by smoothing the objective function with noise and gradually refining the solution. This paper experimentally evaluates the performance of the explicit graduated optimization algorithm with an optimal noise scheduling derived from a previous study and discusses its limitations. It uses traditional benchmark functions and empirical loss functions for modern neural network architectures for evaluating. In addition, this paper extends the implicit graduated optimization algorithm, which is based on the fact that stochastic noise in the optimization process of SGD implicitly smooths the objective function, to SGD with momentum, analyzes its convergence, and demonstrates its effectiveness through experiments on image classification tasks with ResNet architectures.

Scaled Conjugate Gradient Method for Nonconvex Optimization in Deep Neural Networks

A scaled conjugate gradient method that accelerates existing adaptive methods utilizing stochastic gradients is proposed for solving nonconvex optimization problems with deep neural networks. It is shown theoretically that, whether with constant or diminishing learning rates, the proposed method can obtain a stationary point of the problem. Additionally, its rate of convergence with diminishing learning rates is verified to be superior to that of the conjugate gradient method. The proposed method is shown to minimize training loss functions faster than the existing adaptive methods in practical applications of image and text classification. Furthermore, in the training of generative adversarial networks, one version of the proposed method achieved the lowest Frechet inception distance score among those of the adaptive methods.

Convergence of Sharpness-Aware Minimization Algorithms using Increasing Batch Size and Decaying Learning Rate

The sharpness-aware minimization (SAM) algorithm and its variants, including gap guided SAM (GSAM), have been successful at improving the generalization capability of deep neural network models by finding flat local minima of the empirical loss in training. Meanwhile, it has been shown theoretically and practically that increasing the batch size or decaying the learning rate avoids sharp local minima of the empirical loss. In this paper, we consider the GSAM algorithm with increasing batch sizes or decaying learning rates, such as cosine annealing or linear learning rate, and theoretically show its convergence. Moreover, we numerically compare SAM (GSAM) with and without an increasing batch size and conclude that using an increasing batch size or decaying learning rate finds flatter local minima than using a constant batch size and learning rate.

Increasing Both Batch Size and Learning Rate Accelerates Stochastic Gradient Descent

The performance of mini-batch stochastic gradient descent (SGD) strongly depends on setting the batch size and learning rate to minimize the empirical loss in training the deep neural network. In this paper, we present theoretical analyses of mini-batch SGD with four schedulers: (i) constant batch size and decaying learning rate scheduler, (ii) increasing batch size and decaying learning rate scheduler, (iii) increasing batch size and increasing learning rate scheduler, and (iv) increasing batch size and warm-up decaying learning rate scheduler. We show that mini-batch SGD using scheduler (i) does not always minimize the expectation of the full gradient norm of the empirical loss, whereas it does using any of schedulers (ii), (iii), and (iv). Furthermore, schedulers (iii) and (iv) accelerate mini-batch SGD. The paper also provides numerical results of supporting analyses showing that using scheduler (iii) or (iv) minimizes the full gradient norm of the empirical loss faster than using scheduler (i) or (ii).

Iteration and Stochastic First-order Oracle Complexities of Stochastic Gradient Descent using Constant and Decaying Learning Rates

The performance of stochastic gradient descent (SGD), which is the simplest first-order optimizer for training deep neural networks, depends on not only the learning rate but also the batch size. They both affect the number of iterations and the stochastic first-order oracle (SFO) complexity needed for training. In particular, the previous numerical results indicated that, for SGD using a constant learning rate, the number of iterations needed for training decreases when the batch size increases, and the SFO complexity needed for training is minimized at a critical batch size and that it increases once the batch size exceeds that size. Here, we study the relationship between batch size and the iteration and SFO complexities needed for nonconvex optimization in deep learning with SGD using constant or decaying learning rates and show that SGD using the critical batch size minimizes the SFO complexity. We also provide numerical comparisons of SGD with the existing first-order optimizers and show the usefulness of SGD using a critical batch size. Moreover, we show that measured critical batch sizes are close to the sizes estimated from our theoretical results.