Heteroscedastic Double Bayesian Elastic Net

In many practical applications, regression models are employed to uncover relationships between predictors and a response variable, yet the common assumption of constant error variance is frequently violated. This issue is further compounded in high-dimensional settings where the number of predictors exceeds the sample size, necessitating regularization for effective estimation and variable selection. To address this problem, we propose the Heteroscedastic Double Bayesian Elastic Net (HDBEN), a novel framework that jointly models the mean and log-variance using hierarchical Bayesian priors incorporating both $\ell_1$ and $\ell_2$ penalties. Our approach simultaneously induces sparsity and grouping in the regression coefficients and variance parameters, capturing complex variance structures in the data. Theoretical results demonstrate that proposed HDBEN achieves posterior concentration, variable selection consistency, and asymptotic normality under mild conditions which justifying its behavior. Simulation studies further illustrate that HDBEN outperforms existing methods, particularly in scenarios characterized by heteroscedasticity and high dimensionality.

Theoretical and Practical Analysis of Fréchet Regression via Comparison Geometry

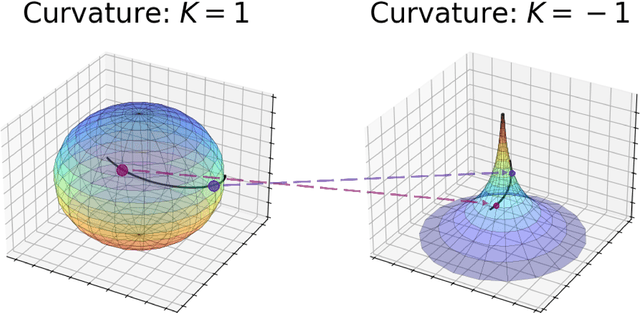
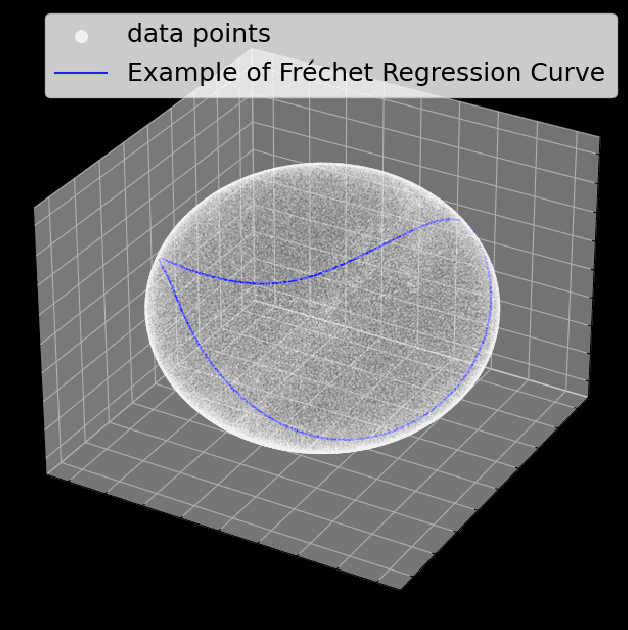
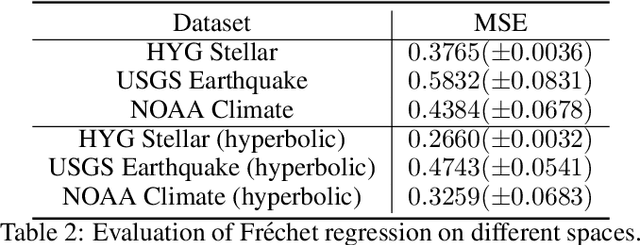
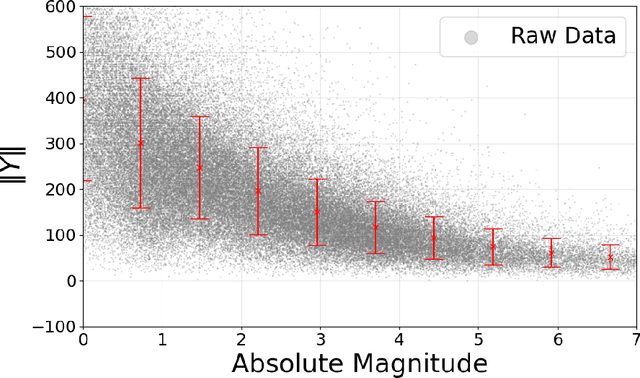
Fr\'echet regression extends classical regression methods to non-Euclidean metric spaces, enabling the analysis of data relationships on complex structures such as manifolds and graphs. This work establishes a rigorous theoretical analysis for Fr\'echet regression through the lens of comparison geometry which leads to important considerations for its use in practice. The analysis provides key results on the existence, uniqueness, and stability of the Fr\'echet mean, along with statistical guarantees for nonparametric regression, including exponential concentration bounds and convergence rates. Additionally, insights into angle stability reveal the interplay between curvature of the manifold and the behavior of the regression estimator in these non-Euclidean contexts. Empirical experiments validate the theoretical findings, demonstrating the effectiveness of proposed hyperbolic mappings, particularly for data with heteroscedasticity, and highlighting the practical usefulness of these results.

A Fashion Item Recommendation Model in Hyperbolic Space

In this work, we propose a fashion item recommendation model that incorporates hyperbolic geometry into user and item representations. Using hyperbolic space, our model aims to capture implicit hierarchies among items based on their visual data and users' purchase history. During training, we apply a multi-task learning framework that considers both hyperbolic and Euclidean distances in the loss function. Our experiments on three data sets show that our model performs better than previous models trained in Euclidean space only, confirming the effectiveness of our model. Our ablation studies show that multi-task learning plays a key role, and removing the Euclidean loss substantially deteriorates the model performance.

Density Ratio Estimation via Sampling along Generalized Geodesics on Statistical Manifolds

The density ratio of two probability distributions is one of the fundamental tools in mathematical and computational statistics and machine learning, and it has a variety of known applications. Therefore, density ratio estimation from finite samples is a very important task, but it is known to be unstable when the distributions are distant from each other. One approach to address this problem is density ratio estimation using incremental mixtures of the two distributions. We geometrically reinterpret existing methods for density ratio estimation based on incremental mixtures. We show that these methods can be regarded as iterating on the Riemannian manifold along a particular curve between the two probability distributions. Making use of the geometry of the manifold, we propose to consider incremental density ratio estimation along generalized geodesics on this manifold. To achieve such a method requires Monte Carlo sampling along geodesics via transformations of the two distributions. We show how to implement an iterative algorithm to sample along these geodesics and show how changing the distances along the geodesic affect the variance and accuracy of the estimation of the density ratio. Our experiments demonstrate that the proposed approach outperforms the existing approaches using incremental mixtures that do not take the geometry of the

Explaining Black-box Model Predictions via Two-level Nested Feature Attributions with Consistency Property

Techniques that explain the predictions of black-box machine learning models are crucial to make the models transparent, thereby increasing trust in AI systems. The input features to the models often have a nested structure that consists of high- and low-level features, and each high-level feature is decomposed into multiple low-level features. For such inputs, both high-level feature attributions (HiFAs) and low-level feature attributions (LoFAs) are important for better understanding the model's decision. In this paper, we propose a model-agnostic local explanation method that effectively exploits the nested structure of the input to estimate the two-level feature attributions simultaneously. A key idea of the proposed method is to introduce the consistency property that should exist between the HiFAs and LoFAs, thereby bridging the separate optimization problems for estimating them. Thanks to this consistency property, the proposed method can produce HiFAs and LoFAs that are both faithful to the black-box models and consistent with each other, using a smaller number of queries to the models. In experiments on image classification in multiple instance learning and text classification using language models, we demonstrate that the HiFAs and LoFAs estimated by the proposed method are accurate, faithful to the behaviors of the black-box models, and provide consistent explanations.

Geometric Insights into Focal Loss: Reducing Curvature for Enhanced Model Calibration

The key factor in implementing machine learning algorithms in decision-making situations is not only the accuracy of the model but also its confidence level. The confidence level of a model in a classification problem is often given by the output vector of a softmax function for convenience. However, these values are known to deviate significantly from the actual expected model confidence. This problem is called model calibration and has been studied extensively. One of the simplest techniques to tackle this task is focal loss, a generalization of cross-entropy by introducing one positive parameter. Although many related studies exist because of the simplicity of the idea and its formalization, the theoretical analysis of its behavior is still insufficient. In this study, our objective is to understand the behavior of focal loss by reinterpreting this function geometrically. Our analysis suggests that focal loss reduces the curvature of the loss surface in training the model. This indicates that curvature may be one of the essential factors in achieving model calibration. We design numerical experiments to support this conjecture to reveal the behavior of focal loss and the relationship between calibration performance and curvature.

On permutation-invariant neural networks

Conventional machine learning algorithms have traditionally been designed under the assumption that input data follows a vector-based format, with an emphasis on vector-centric paradigms. However, as the demand for tasks involving set-based inputs has grown, there has been a paradigm shift in the research community towards addressing these challenges. In recent years, the emergence of neural network architectures such as Deep Sets and Transformers has presented a significant advancement in the treatment of set-based data. These architectures are specifically engineered to naturally accommodate sets as input, enabling more effective representation and processing of set structures. Consequently, there has been a surge of research endeavors dedicated to exploring and harnessing the capabilities of these architectures for various tasks involving the approximation of set functions. This comprehensive survey aims to provide an overview of the diverse problem settings and ongoing research efforts pertaining to neural networks that approximate set functions. By delving into the intricacies of these approaches and elucidating the associated challenges, the survey aims to equip readers with a comprehensive understanding of the field. Through this comprehensive perspective, we hope that researchers can gain valuable insights into the potential applications, inherent limitations, and future directions of set-based neural networks. Indeed, from this survey we gain two insights: i) Deep Sets and its variants can be generalized by differences in the aggregation function, and ii) the behavior of Deep Sets is sensitive to the choice of the aggregation function. From these observations, we show that Deep Sets, one of the well-known permutation-invariant neural networks, can be generalized in the sense of a quasi-arithmetic mean.

A Short Survey on Importance Weighting for Machine Learning

Importance weighting is a fundamental procedure in statistics and machine learning that weights the objective function or probability distribution based on the importance of the instance in some sense. The simplicity and usefulness of the idea has led to many applications of importance weighting. For example, it is known that supervised learning under an assumption about the difference between the training and test distributions, called distribution shift, can guarantee statistically desirable properties through importance weighting by their density ratio. This survey summarizes the broad applications of importance weighting in machine learning and related research.

Understanding Test-Time Augmentation

Test-Time Augmentation (TTA) is a very powerful heuristic that takes advantage of data augmentation during testing to produce averaged output. Despite the experimental effectiveness of TTA, there is insufficient discussion of its theoretical aspects. In this paper, we aim to give theoretical guarantees for TTA and clarify its behavior.

Information Geometrically Generalized Covariate Shift Adaptation

Many machine learning methods assume that the training and test data follow the same distribution. However, in the real world, this assumption is very often violated. In particular, the phenomenon that the marginal distribution of the data changes is called covariate shift, one of the most important research topics in machine learning. We show that the well-known family of covariate shift adaptation methods is unified in the framework of information geometry. Furthermore, we show that parameter search for geometrically generalized covariate shift adaptation method can be achieved efficiently. Numerical experiments show that our generalization can achieve better performance than the existing methods it encompasses.