Howard Bondell
Generalized Power Priors for Improved Bayesian Inference with Historical Data
May 22, 2025Abstract:The power prior is a class of informative priors designed to incorporate historical data alongside current data in a Bayesian framework. It includes a power parameter that controls the influence of historical data, providing flexibility and adaptability. A key property of the power prior is that the resulting posterior minimizes a linear combination of KL divergences between two pseudo-posterior distributions: one ignoring historical data and the other fully incorporating it. We extend this framework by identifying the posterior distribution as the minimizer of a linear combination of Amari's $\alpha$-divergence, a generalization of KL divergence. We show that this generalization can lead to improved performance by allowing for the data to adapt to appropriate choices of the $\alpha$ parameter. Theoretical properties of this generalized power posterior are established, including behavior as a generalized geodesic on the Riemannian manifold of probability distributions, offering novel insights into its geometric interpretation.
Theoretical and Practical Analysis of Fréchet Regression via Comparison Geometry
Feb 04, 2025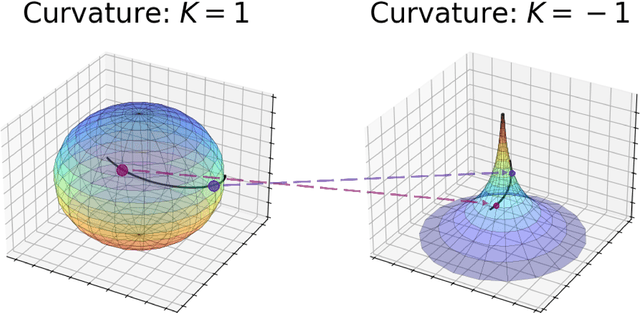
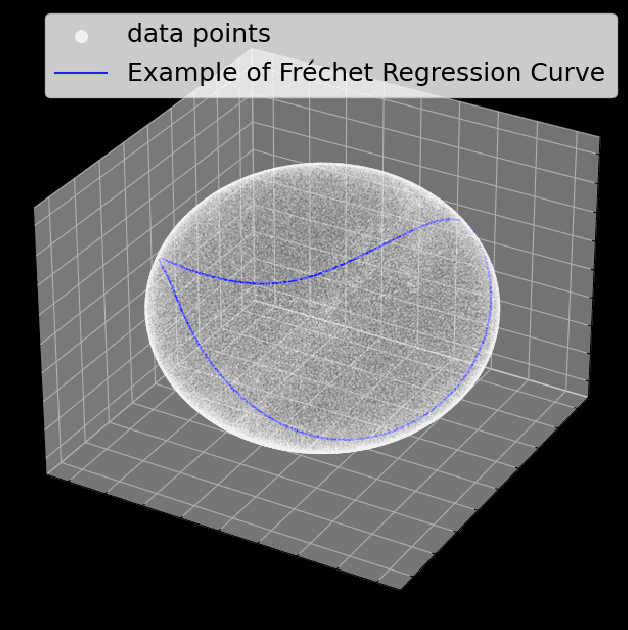
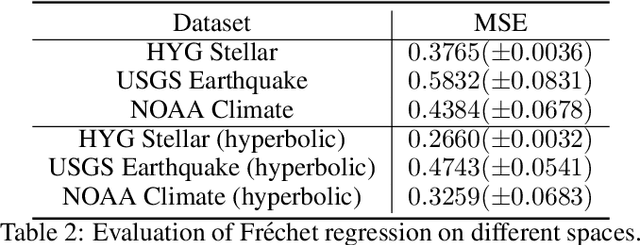
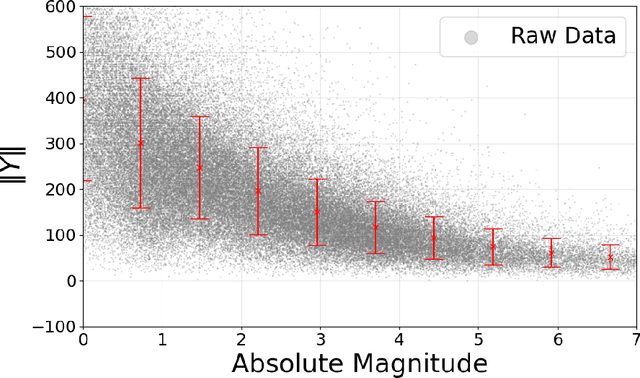
Abstract:Fr\'echet regression extends classical regression methods to non-Euclidean metric spaces, enabling the analysis of data relationships on complex structures such as manifolds and graphs. This work establishes a rigorous theoretical analysis for Fr\'echet regression through the lens of comparison geometry which leads to important considerations for its use in practice. The analysis provides key results on the existence, uniqueness, and stability of the Fr\'echet mean, along with statistical guarantees for nonparametric regression, including exponential concentration bounds and convergence rates. Additionally, insights into angle stability reveal the interplay between curvature of the manifold and the behavior of the regression estimator in these non-Euclidean contexts. Empirical experiments validate the theoretical findings, demonstrating the effectiveness of proposed hyperbolic mappings, particularly for data with heteroscedasticity, and highlighting the practical usefulness of these results.
Faithful Label-free Knowledge Distillation
Nov 22, 2024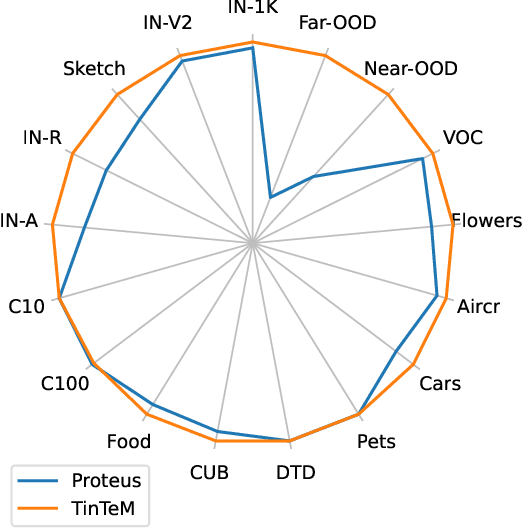
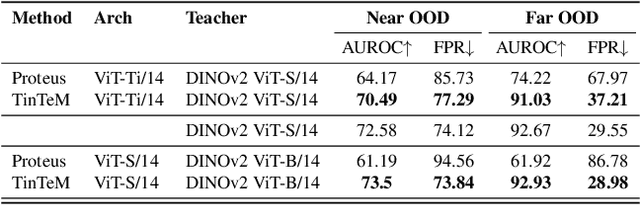

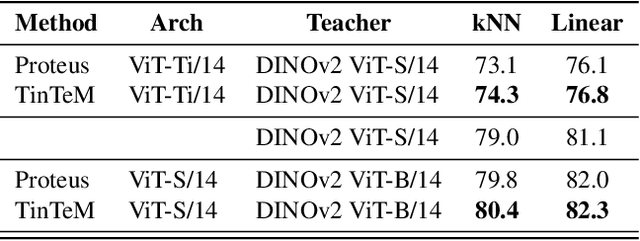
Abstract:Knowledge distillation approaches are model compression techniques, with the goal of training a highly performant student model by using a teacher network that is larger or contains a different inductive bias. These approaches are particularly useful when applied to large computer vision foundation models, which can be compressed into smaller variants that retain desirable properties such as improved robustness. This paper presents a label-free knowledge distillation approach called Teacher in the Middle (TinTeM), which improves on previous methods by learning an approximately orthogonal mapping from the latent space of the teacher to the student network. This produces a more faithful student, which better replicates the behavior of the teacher network across a range of benchmarks testing model robustness, generalisability and out-of-distribution detection. It is further shown that knowledge distillation with TinTeM on task specific datasets leads to more accurate models with greater generalisability and OOD detection performance, and that this technique provides a competitive pathway for training highly performant lightweight models on small datasets.
Density Ratio Estimation via Sampling along Generalized Geodesics on Statistical Manifolds
Jun 27, 2024



Abstract:The density ratio of two probability distributions is one of the fundamental tools in mathematical and computational statistics and machine learning, and it has a variety of known applications. Therefore, density ratio estimation from finite samples is a very important task, but it is known to be unstable when the distributions are distant from each other. One approach to address this problem is density ratio estimation using incremental mixtures of the two distributions. We geometrically reinterpret existing methods for density ratio estimation based on incremental mixtures. We show that these methods can be regarded as iterating on the Riemannian manifold along a particular curve between the two probability distributions. Making use of the geometry of the manifold, we propose to consider incremental density ratio estimation along generalized geodesics on this manifold. To achieve such a method requires Monte Carlo sampling along geodesics via transformations of the two distributions. We show how to implement an iterative algorithm to sample along these geodesics and show how changing the distances along the geodesic affect the variance and accuracy of the estimation of the density ratio. Our experiments demonstrate that the proposed approach outperforms the existing approaches using incremental mixtures that do not take the geometry of the
Scalable and Robust Transformer Decoders for Interpretable Image Classification with Foundation Models
Mar 07, 2024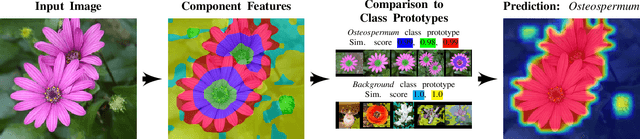
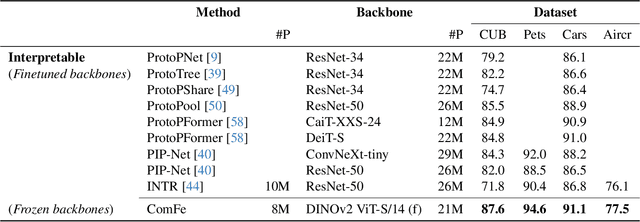
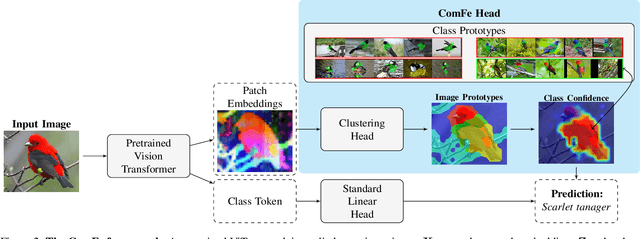
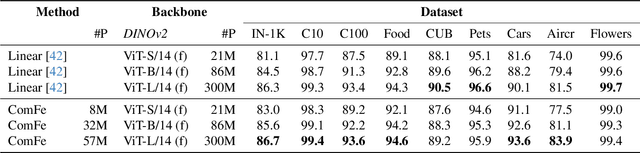
Abstract:Interpretable computer vision models can produce transparent predictions, where the features of an image are compared with prototypes from a training dataset and the similarity between them forms a basis for classification. Nevertheless these methods are computationally expensive to train, introduce additional complexity and may require domain knowledge to adapt hyper-parameters to a new dataset. Inspired by developments in object detection, segmentation and large-scale self-supervised foundation vision models, we introduce Component Features (ComFe), a novel explainable-by-design image classification approach using a transformer-decoder head and hierarchical mixture-modelling. With only global image labels and no segmentation or part annotations, ComFe can identify consistent image components, such as the head, body, wings and tail of a bird, and the image background, and determine which of these features are informative in making a prediction. We demonstrate that ComFe obtains higher accuracy compared to previous interpretable models across a range of fine-grained vision benchmarks, without the need to individually tune hyper-parameters for each dataset. We also show that ComFe outperforms a non-interpretable linear head across a range of datasets, including ImageNet, and improves performance on generalisation and robustness benchmarks.
Improved Prototypical Semi-Supervised Learning with Foundation Models: Prototype Selection, Parametric vMF-SNE Pretraining and Multi-view Pseudolabelling
Nov 28, 2023Abstract:In this paper we present an improved approach to prototypical semi-supervised learning for computer vision, in the context of leveraging a frozen foundation model as the backbone of our neural network. As a general tool, we propose parametric von-Mises Fisher Stochastic Neighbour Embedding (vMF-SNE) to create mappings with neural networks between high-dimensional latent spaces that preserve local structure. This enables us to pretrain the projection head of our network using the high-quality embeddings of the foundation model with vMF-SNE. We also propose soft multi-view pseudolabels, where predictions across multiple views are combined to provide a more reliable supervision signal compared to a consistency or swapped assignment approach. We demonstrate that these ideas improve upon P}redicting View-Assignments with Support Samples (PAWS), a current state-of-the-art semi-supervised learning method, as well as Robust PAWS (RoPAWS), over a range of benchmarking datasets. We also introduce simple $k$-means prototype selection, a technique that provides superior performance to other unsupervised label selection approaches in this context. These changes improve upon PAWS by an average of +2.9% for CIFAR-10 and +5.7% for CIFAR-100 with four labels per class, and by +15.2% for DeepWeeds, a particularly challenging dataset for semi-supervised learning. We also achieve new state-of-the-art results in semi-supervised learning in this small label regime for CIFAR-10 - 95.8% (+0.7%) and CIFAR-100 - 76.6% (+12.0%).
Sparse high-dimensional linear regression with a partitioned empirical Bayes ECM algorithm
Sep 20, 2022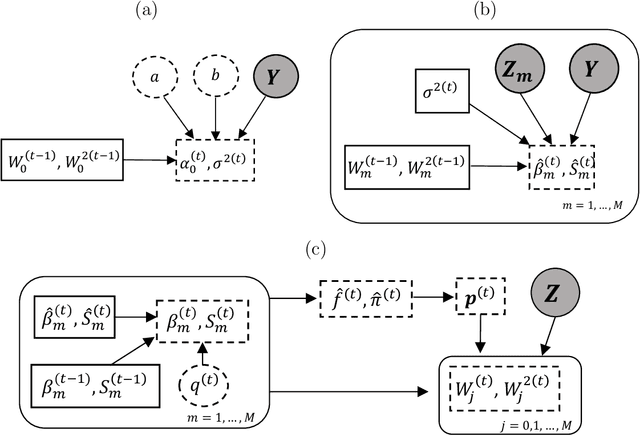
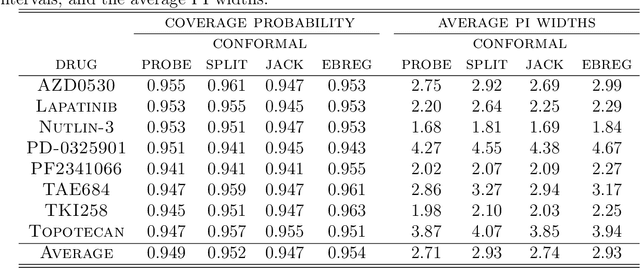
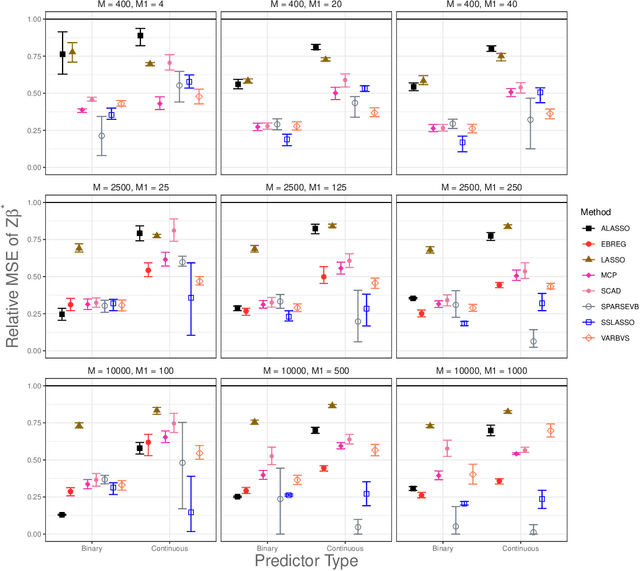
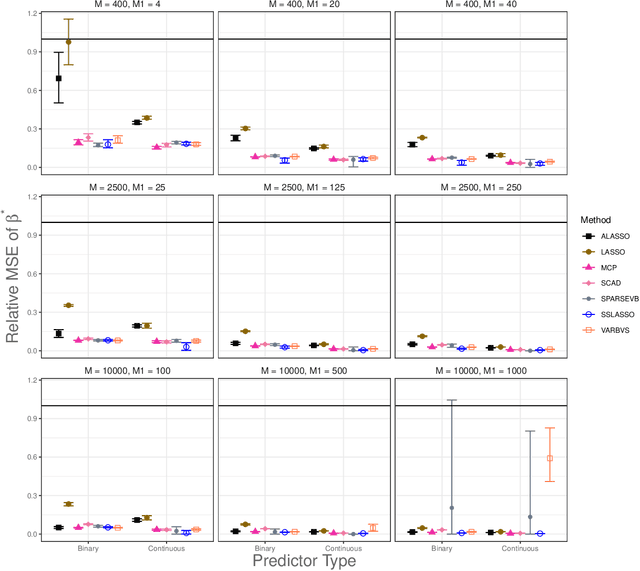
Abstract:Bayesian variable selection methods are powerful techniques for fitting and inferring on sparse high-dimensional linear regression models. However, many are computationally intensive or require restrictive prior distributions on model parameters. Likelihood based penalization methods are more computationally friendly, but resource intensive refitting techniques are needed for inference. In this paper, we proposed an efficient and powerful Bayesian approach for sparse high-dimensional linear regression. Minimal prior assumptions on the parameters are required through the use of plug-in empirical Bayes estimates of hyperparameters. Efficient maximum a posteriori probability (MAP) estimation is completed through the use of a partitioned and extended expectation conditional maximization (ECM) algorithm. The result is a PaRtitiOned empirical Bayes Ecm (PROBE) algorithm applied to sparse high-dimensional linear regression. We propose methods to estimate credible and prediction intervals for predictions of future values. We compare the empirical properties of predictions and our predictive inference to comparable approaches with numerous simulation studies and an analysis of cancer cell lines drug response study. The proposed approach is implemented in the R package probe.
MissDAG: Causal Discovery in the Presence of Missing Data with Continuous Additive Noise Models
May 27, 2022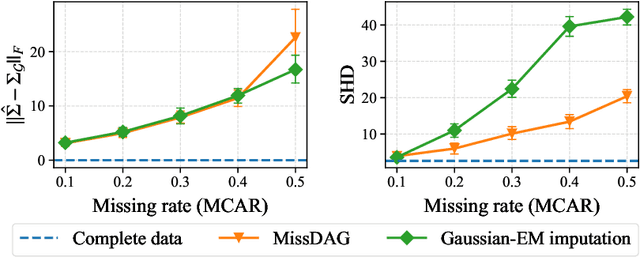
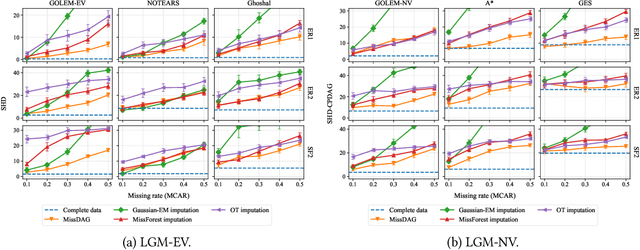
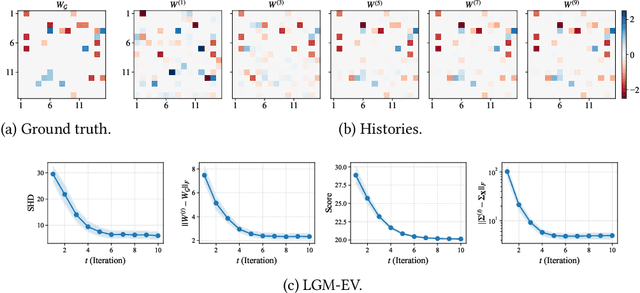
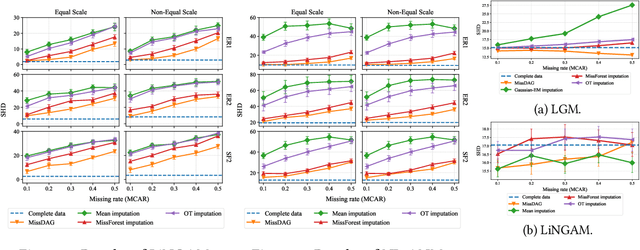
Abstract:State-of-the-art causal discovery methods usually assume that the observational data is complete. However, the missing data problem is pervasive in many practical scenarios such as clinical trials, economics, and biology. One straightforward way to address the missing data problem is first to impute the data using off-the-shelf imputation methods and then apply existing causal discovery methods. However, such a two-step method may suffer from suboptimality, as the imputation algorithm is unaware of the causal discovery step. In this paper, we develop a general method, which we call MissDAG, to perform causal discovery from data with incomplete observations. Focusing mainly on the assumptions of ignorable missingness and the identifiable additive noise models (ANMs), MissDAG maximizes the expected likelihood of the visible part of observations under the expectation-maximization (EM) framework. In the E-step, in cases where computing the posterior distributions of parameters in closed-form is not feasible, Monte Carlo EM is leveraged to approximate the likelihood. In the M-step, MissDAG leverages the density transformation to model the noise distributions with simpler and specific formulations by virtue of the ANMs and uses a likelihood-based causal discovery algorithm with directed acyclic graph prior as an inductive bias. We demonstrate the flexibility of MissDAG for incorporating various causal discovery algorithms and its efficacy through extensive simulations and real data experiments.
Federated Causal Discovery
Dec 07, 2021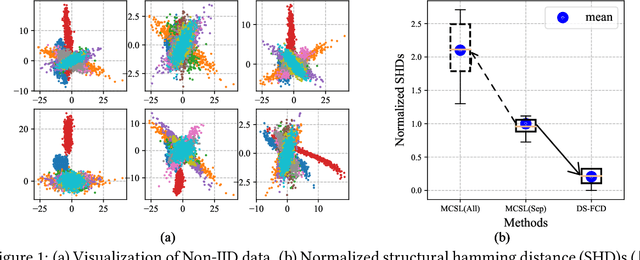
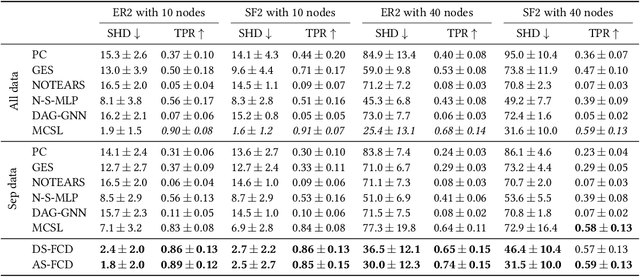
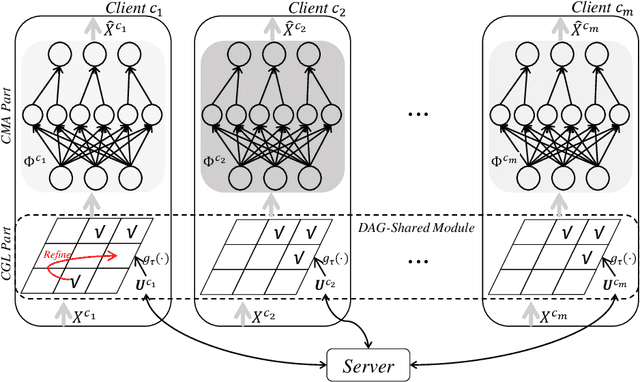
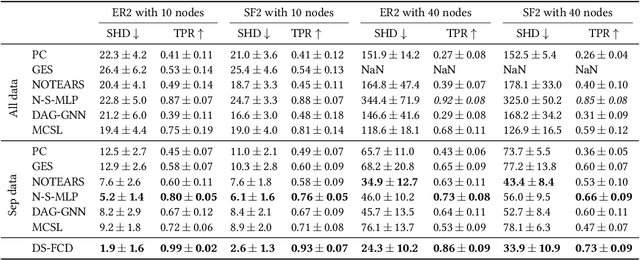
Abstract:Causal discovery aims to learn a causal graph from observational data. To date, most causal discovery methods require data to be stored in a central server. However, data owners gradually refuse to share their personalized data to avoid privacy leakage, making this task more troublesome by cutting off the first step. A puzzle arises: $\textit{how do we infer causal relations from decentralized data?}$ In this paper, with the additive noise model assumption of data, we take the first step in developing a gradient-based learning framework named DAG-Shared Federated Causal Discovery (DS-FCD), which can learn the causal graph without directly touching local data and naturally handle the data heterogeneity. DS-FCD benefits from a two-level structure of each local model. The first level learns the causal graph and communicates with the server to get model information from other clients, while the second level approximates causal mechanisms and personally updates from its own data to accommodate the data heterogeneity. Moreover, DS-FCD formulates the overall learning task as a continuous optimization problem by taking advantage of an equality acyclicity constraint, which can be naturally solved by gradient descent methods. Extensive experiments on both synthetic and real-world datasets verify the efficacy of the proposed method.
Variational approximations using Fisher divergence
May 13, 2019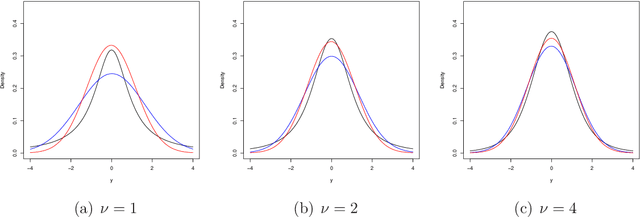
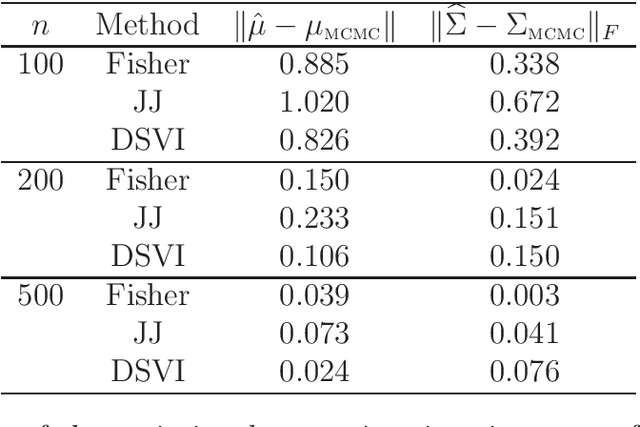
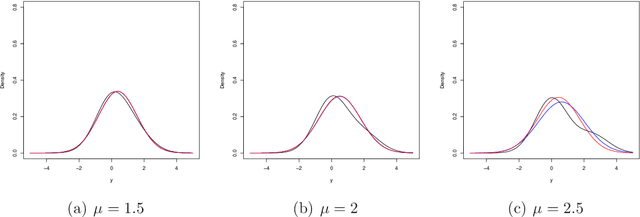
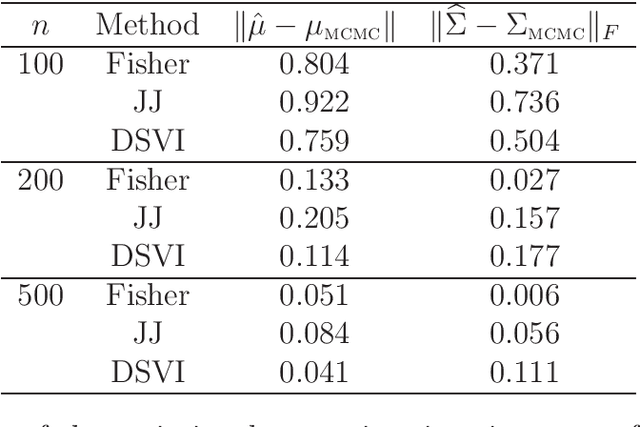
Abstract:Modern applications of Bayesian inference involve models that are sufficiently complex that the corresponding posterior distributions are intractable and must be approximated. The most common approximation is based on Markov chain Monte Carlo, but these can be expensive when the data set is large and/or the model is complex, so more efficient variational approximations have recently received considerable attention. The traditional variational methods, that seek to minimize the Kullback--Leibler divergence between the posterior and a relatively simple parametric family, provide accurate and efficient estimation of the posterior mean, but often does not capture other moments, and have limitations in terms of the models to which they can be applied. Here we propose the construction of variational approximations based on minimizing the Fisher divergence, and develop an efficient computational algorithm that can be applied to a wide range of models without conjugacy or potentially unrealistic mean-field assumptions. We demonstrate the superior performance of the proposed method for the benchmark case of logistic regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge