Variational approximations of empirical Bayes posteriors in high-dimensional linear models

In high-dimensions, the prior tails can have a significant effect on both posterior computation and asymptotic concentration rates. To achieve optimal rates while keeping the posterior computations relatively simple, an empirical Bayes approach has recently been proposed, featuring thin-tailed conjugate priors with data-driven centers. While conjugate priors ease some of the computational burden, Markov chain Monte Carlo methods are still needed, which can be expensive when dimension is high. In this paper, we develop a variational approximation to the empirical Bayes posterior that is fast to compute and retains the optimal concentration rate properties of the original. In simulations, our method is shown to have superior performance compared to existing variational approximations in the literature across a wide range of high-dimensional settings.

Valid distribution-free inferential models for prediction

A fundamental problem in statistics and machine learning is that of using observed data to predict future observations. This is particularly challenging for model-based approaches because often the goal is to carry out this prediction with no or minimal model assumptions. For example, the inferential model (IM) approach is attractive because it has certain validity guarantees, but requires specification of a parametric model. Here we show that a new perspective on a recently developed generalized IM approach can be applied to construct an IM for prediction that satisfies the desirable validity guarantees without specification of a model. One important special case of this approach corresponds to the powerful conformal prediction framework and, consequently, the desirable properties of conformal prediction follow immediately from the general IM validity theory. Several numerical examples are presented to illustrate the theory and highlight the method's performance and flexibility.

Variational approximations using Fisher divergence

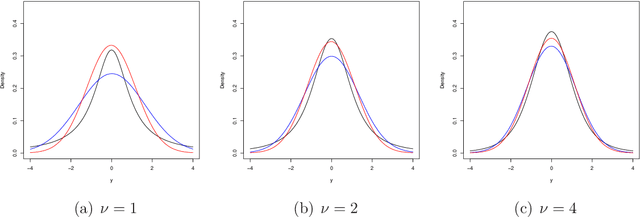
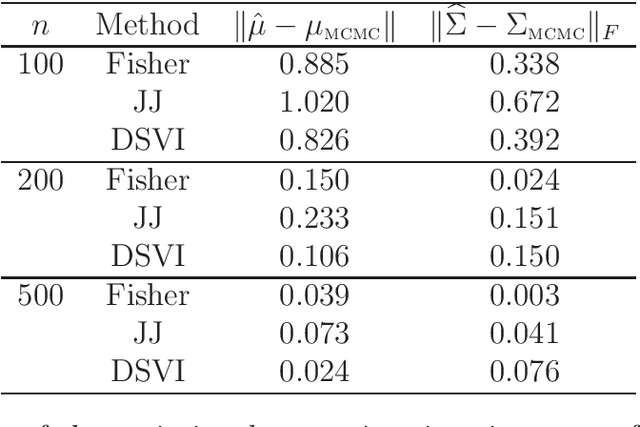
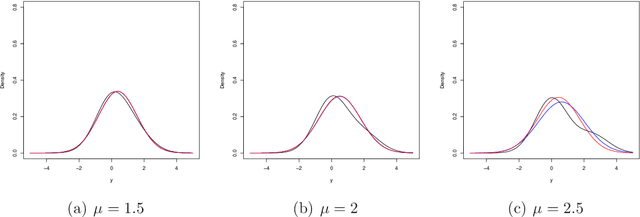
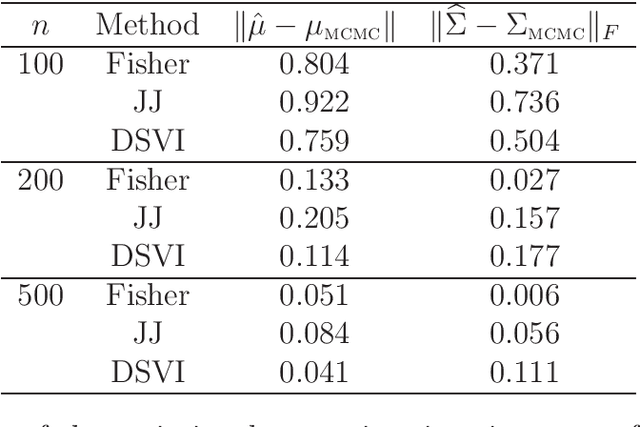
Modern applications of Bayesian inference involve models that are sufficiently complex that the corresponding posterior distributions are intractable and must be approximated. The most common approximation is based on Markov chain Monte Carlo, but these can be expensive when the data set is large and/or the model is complex, so more efficient variational approximations have recently received considerable attention. The traditional variational methods, that seek to minimize the Kullback--Leibler divergence between the posterior and a relatively simple parametric family, provide accurate and efficient estimation of the posterior mean, but often does not capture other moments, and have limitations in terms of the models to which they can be applied. Here we propose the construction of variational approximations based on minimizing the Fisher divergence, and develop an efficient computational algorithm that can be applied to a wide range of models without conjugacy or potentially unrealistic mean-field assumptions. We demonstrate the superior performance of the proposed method for the benchmark case of logistic regression.

On epsilon-optimality of the pursuit learning algorithm

Estimator algorithms in learning automata are useful tools for adaptive, real-time optimization in computer science and engineering applications. This paper investigates theoretical convergence properties for a special case of estimator algorithms: the pursuit learning algorithm. In this note, we identify and fill a gap in existing proofs of probabilistic convergence for pursuit learning. It is tradition to take the pursuit learning tuning parameter to be fixed in practical applications, but our proof sheds light on the importance of a vanishing sequence of tuning parameters in a theoretical convergence analysis.