Spectral Estimation with Free Decompression

Computing eigenvalues of very large matrices is a critical task in many machine learning applications, including the evaluation of log-determinants, the trace of matrix functions, and other important metrics. As datasets continue to grow in scale, the corresponding covariance and kernel matrices become increasingly large, often reaching magnitudes that make their direct formation impractical or impossible. Existing techniques typically rely on matrix-vector products, which can provide efficient approximations, if the matrix spectrum behaves well. However, in settings like distributed learning, or when the matrix is defined only indirectly, access to the full data set can be restricted to only very small sub-matrices of the original matrix. In these cases, the matrix of nominal interest is not even available as an implicit operator, meaning that even matrix-vector products may not be available. In such settings, the matrix is "impalpable," in the sense that we have access to only masked snapshots of it. We draw on principles from free probability theory to introduce a novel method of "free decompression" to estimate the spectrum of such matrices. Our method can be used to extrapolate from the empirical spectral densities of small submatrices to infer the eigenspectrum of extremely large (impalpable) matrices (that we cannot form or even evaluate with full matrix-vector products). We demonstrate the effectiveness of this approach through a series of examples, comparing its performance against known limiting distributions from random matrix theory in synthetic settings, as well as applying it to submatrices of real-world datasets, matching them with their full empirical eigenspectra.

Determinant Estimation under Memory Constraints and Neural Scaling Laws

Calculating or accurately estimating log-determinants of large positive semi-definite matrices is of fundamental importance in many machine learning tasks. While its cubic computational complexity can already be prohibitive, in modern applications, even storing the matrices themselves can pose a memory bottleneck. To address this, we derive a novel hierarchical algorithm based on block-wise computation of the LDL decomposition for large-scale log-determinant calculation in memory-constrained settings. In extreme cases where matrices are highly ill-conditioned, accurately computing the full matrix itself may be infeasible. This is particularly relevant when considering kernel matrices at scale, including the empirical Neural Tangent Kernel (NTK) of neural networks trained on large datasets. Under the assumption of neural scaling laws in the test error, we show that the ratio of pseudo-determinants satisfies a power-law relationship, allowing us to derive corresponding scaling laws. This enables accurate estimation of NTK log-determinants from a tiny fraction of the full dataset; in our experiments, this results in a $\sim$100,000$\times$ speedup with improved accuracy over competing approximations. Using these techniques, we successfully estimate log-determinants for dense matrices of extreme sizes, which were previously deemed intractable and inaccessible due to their enormous scale and computational demands.

Uncertainty Quantification with the Empirical Neural Tangent Kernel

While neural networks have demonstrated impressive performance across various tasks, accurately quantifying uncertainty in their predictions is essential to ensure their trustworthiness and enable widespread adoption in critical systems. Several Bayesian uncertainty quantification (UQ) methods exist that are either cheap or reliable, but not both. We propose a post-hoc, sampling-based UQ method for over-parameterized networks at the end of training. Our approach constructs efficient and meaningful deep ensembles by employing a (stochastic) gradient-descent sampling process on appropriately linearized networks. We demonstrate that our method effectively approximates the posterior of a Gaussian process using the empirical Neural Tangent Kernel. Through a series of numerical experiments, we show that our method not only outperforms competing approaches in computational efficiency (often reducing costs by multiple factors) but also maintains state-of-the-art performance across a variety of UQ metrics for both regression and classification tasks.

Faithful Label-free Knowledge Distillation

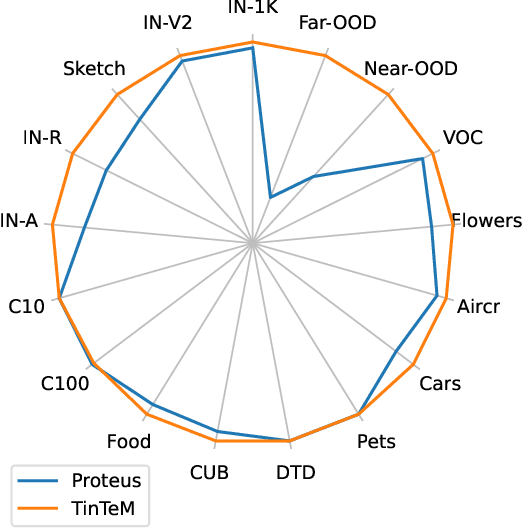
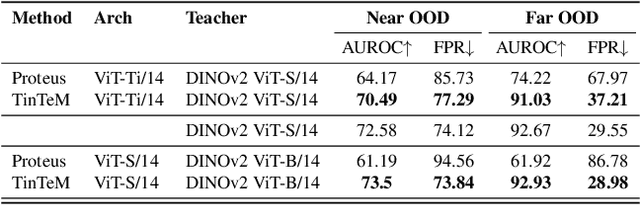
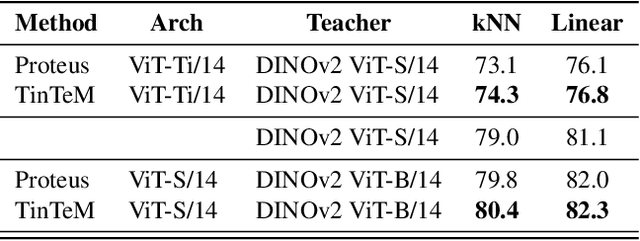
Knowledge distillation approaches are model compression techniques, with the goal of training a highly performant student model by using a teacher network that is larger or contains a different inductive bias. These approaches are particularly useful when applied to large computer vision foundation models, which can be compressed into smaller variants that retain desirable properties such as improved robustness. This paper presents a label-free knowledge distillation approach called Teacher in the Middle (TinTeM), which improves on previous methods by learning an approximately orthogonal mapping from the latent space of the teacher to the student network. This produces a more faithful student, which better replicates the behavior of the teacher network across a range of benchmarks testing model robustness, generalisability and out-of-distribution detection. It is further shown that knowledge distillation with TinTeM on task specific datasets leads to more accurate models with greater generalisability and OOD detection performance, and that this technique provides a competitive pathway for training highly performant lightweight models on small datasets.

How many classifiers do we need?

As performance gains through scaling data and/or model size experience diminishing returns, it is becoming increasingly popular to turn to ensembling, where the predictions of multiple models are combined to improve accuracy. In this paper, we provide a detailed analysis of how the disagreement and the polarization (a notion we introduce and define in this paper) among classifiers relate to the performance gain achieved by aggregating individual classifiers, for majority vote strategies in classification tasks. We address these questions in the following ways. (1) An upper bound for polarization is derived, and we propose what we call a neural polarization law: most interpolating neural network models are 4/3-polarized. Our empirical results not only support this conjecture but also show that polarization is nearly constant for a dataset, regardless of hyperparameters or architectures of classifiers. (2) The error of the majority vote classifier is considered under restricted entropy conditions, and we present a tight upper bound that indicates that the disagreement is linearly correlated with the target, and that the slope is linear in the polarization. (3) We prove results for the asymptotic behavior of the disagreement in terms of the number of classifiers, which we show can help in predicting the performance for a larger number of classifiers from that of a smaller number. Our theories and claims are supported by empirical results on several image classification tasks with various types of neural networks.

Temperature Optimization for Bayesian Deep Learning

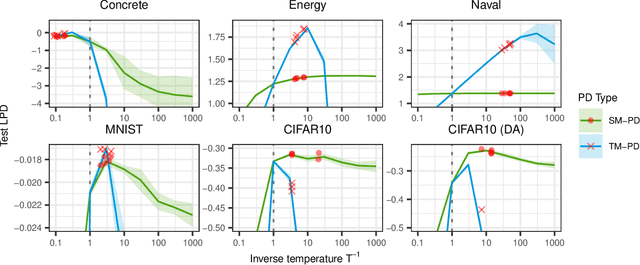
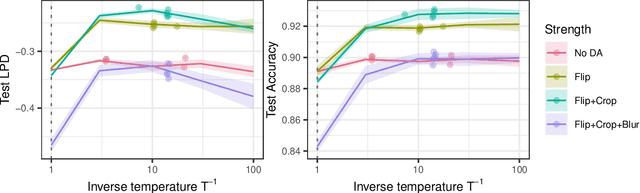
The Cold Posterior Effect (CPE) is a phenomenon in Bayesian Deep Learning (BDL), where tempering the posterior to a cold temperature often improves the predictive performance of the posterior predictive distribution (PPD). Although the term `CPE' suggests colder temperatures are inherently better, the BDL community increasingly recognizes that this is not always the case. Despite this, there remains no systematic method for finding the optimal temperature beyond grid search. In this work, we propose a data-driven approach to select the temperature that maximizes test log-predictive density, treating the temperature as a model parameter and estimating it directly from the data. We empirically demonstrate that our method performs comparably to grid search, at a fraction of the cost, across both regression and classification tasks. Finally, we highlight the differing perspectives on CPE between the BDL and Generalized Bayes communities: while the former primarily focuses on predictive performance of the PPD, the latter emphasizes calibrated uncertainty and robustness to model misspecification; these distinct objectives lead to different temperature preferences.

A PAC-Bayesian Perspective on the Interpolating Information Criterion

Deep learning is renowned for its theory-practice gap, whereby principled theory typically fails to provide much beneficial guidance for implementation in practice. This has been highlighted recently by the benign overfitting phenomenon: when neural networks become sufficiently large to interpolate the dataset perfectly, model performance appears to improve with increasing model size, in apparent contradiction with the well-known bias-variance tradeoff. While such phenomena have proven challenging to theoretically study for general models, the recently proposed Interpolating Information Criterion (IIC) provides a valuable theoretical framework to examine performance for overparameterized models. Using the IIC, a PAC-Bayes bound is obtained for a general class of models, characterizing factors which influence generalization performance in the interpolating regime. From the provided bound, we quantify how the test error for overparameterized models achieving effectively zero training error depends on the quality of the implicit regularization imposed by e.g. the combination of model, optimizer, and parameter-initialization scheme; the spectrum of the empirical neural tangent kernel; curvature of the loss landscape; and noise present in the data.

The Interpolating Information Criterion for Overparameterized Models

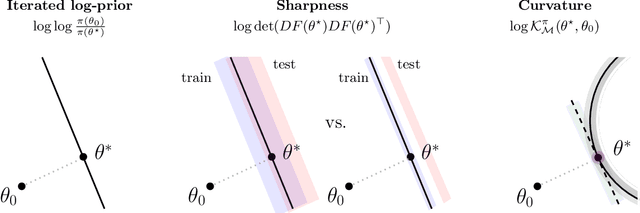
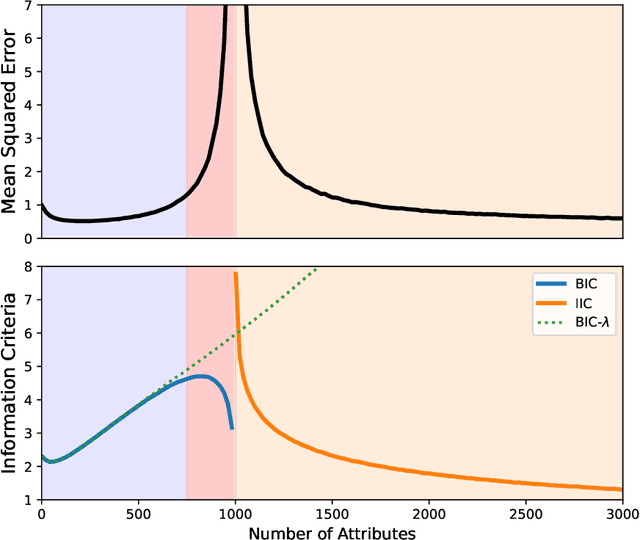
The problem of model selection is considered for the setting of interpolating estimators, where the number of model parameters exceeds the size of the dataset. Classical information criteria typically consider the large-data limit, penalizing model size. However, these criteria are not appropriate in modern settings where overparameterized models tend to perform well. For any overparameterized model, we show that there exists a dual underparameterized model that possesses the same marginal likelihood, thus establishing a form of Bayesian duality. This enables more classical methods to be used in the overparameterized setting, revealing the Interpolating Information Criterion, a measure of model quality that naturally incorporates the choice of prior into the model selection. Our new information criterion accounts for prior misspecification, geometric and spectral properties of the model, and is numerically consistent with known empirical and theoretical behavior in this regime.

Generalization Guarantees via Algorithm-dependent Rademacher Complexity

Algorithm- and data-dependent generalization bounds are required to explain the generalization behavior of modern machine learning algorithms. In this context, there exists information theoretic generalization bounds that involve (various forms of) mutual information, as well as bounds based on hypothesis set stability. We propose a conceptually related, but technically distinct complexity measure to control generalization error, which is the empirical Rademacher complexity of an algorithm- and data-dependent hypothesis class. Combining standard properties of Rademacher complexity with the convenient structure of this class, we are able to (i) obtain novel bounds based on the finite fractal dimension, which (a) extend previous fractal dimension-type bounds from continuous to finite hypothesis classes, and (b) avoid a mutual information term that was required in prior work; (ii) we greatly simplify the proof of a recent dimension-independent generalization bound for stochastic gradient descent; and (iii) we easily recover results for VC classes and compression schemes, similar to approaches based on conditional mutual information.

A Heavy-Tailed Algebra for Probabilistic Programming

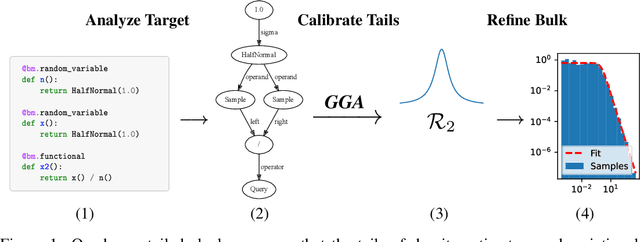
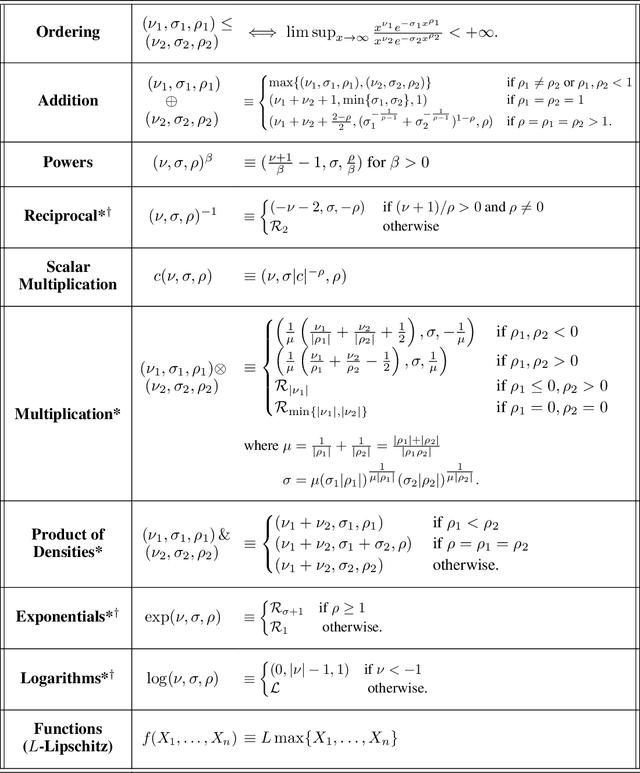
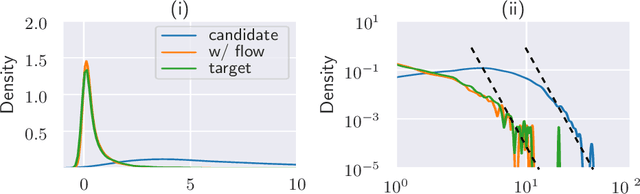
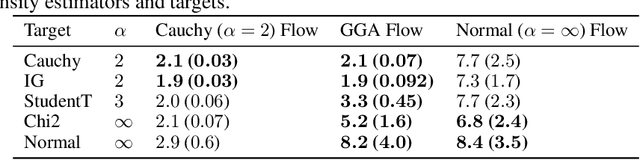
Despite the successes of probabilistic models based on passing noise through neural networks, recent work has identified that such methods often fail to capture tail behavior accurately, unless the tails of the base distribution are appropriately calibrated. To overcome this deficiency, we propose a systematic approach for analyzing the tails of random variables, and we illustrate how this approach can be used during the static analysis (before drawing samples) pass of a probabilistic programming language compiler. To characterize how the tails change under various operations, we develop an algebra which acts on a three-parameter family of tail asymptotics and which is based on the generalized Gamma distribution. Our algebraic operations are closed under addition and multiplication; they are capable of distinguishing sub-Gaussians with differing scales; and they handle ratios sufficiently well to reproduce the tails of most important statistical distributions directly from their definitions. Our empirical results confirm that inference algorithms that leverage our heavy-tailed algebra attain superior performance across a number of density modeling and variational inference tasks.