How many classifiers do we need?

As performance gains through scaling data and/or model size experience diminishing returns, it is becoming increasingly popular to turn to ensembling, where the predictions of multiple models are combined to improve accuracy. In this paper, we provide a detailed analysis of how the disagreement and the polarization (a notion we introduce and define in this paper) among classifiers relate to the performance gain achieved by aggregating individual classifiers, for majority vote strategies in classification tasks. We address these questions in the following ways. (1) An upper bound for polarization is derived, and we propose what we call a neural polarization law: most interpolating neural network models are 4/3-polarized. Our empirical results not only support this conjecture but also show that polarization is nearly constant for a dataset, regardless of hyperparameters or architectures of classifiers. (2) The error of the majority vote classifier is considered under restricted entropy conditions, and we present a tight upper bound that indicates that the disagreement is linearly correlated with the target, and that the slope is linear in the polarization. (3) We prove results for the asymptotic behavior of the disagreement in terms of the number of classifiers, which we show can help in predicting the performance for a larger number of classifiers from that of a smaller number. Our theories and claims are supported by empirical results on several image classification tasks with various types of neural networks.

When are ensembles really effective?

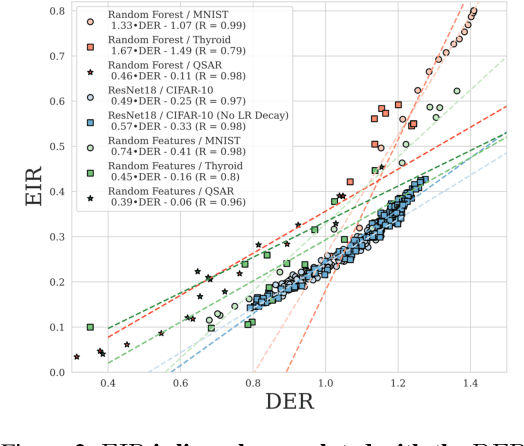
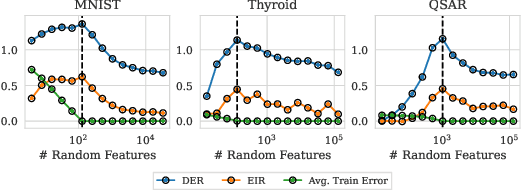
Ensembling has a long history in statistical data analysis, with many impactful applications. However, in many modern machine learning settings, the benefits of ensembling are less ubiquitous and less obvious. We study, both theoretically and empirically, the fundamental question of when ensembling yields significant performance improvements in classification tasks. Theoretically, we prove new results relating the \emph{ensemble improvement rate} (a measure of how much ensembling decreases the error rate versus a single model, on a relative scale) to the \emph{disagreement-error ratio}. We show that ensembling improves performance significantly whenever the disagreement rate is large relative to the average error rate; and that, conversely, one classifier is often enough whenever the disagreement rate is low relative to the average error rate. On the way to proving these results, we derive, under a mild condition called \emph{competence}, improved upper and lower bounds on the average test error rate of the majority vote classifier. To complement this theory, we study ensembling empirically in a variety of settings, verifying the predictions made by our theory, and identifying practical scenarios where ensembling does and does not result in large performance improvements. Perhaps most notably, we demonstrate a distinct difference in behavior between interpolating models (popular in current practice) and non-interpolating models (such as tree-based methods, where ensembling is popular), demonstrating that ensembling helps considerably more in the latter case than in the former.