When are ensembles really effective?
Paper and Code
May 21, 2023

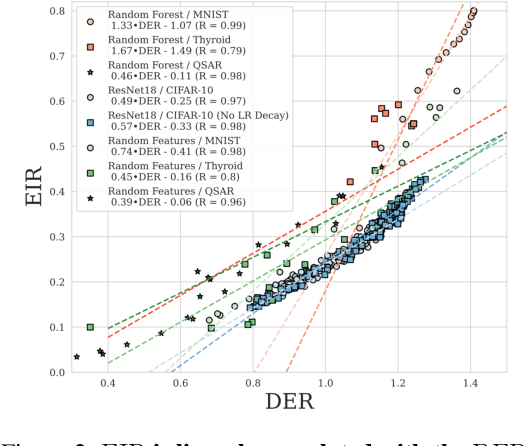
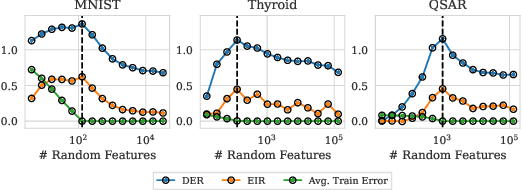
Ensembling has a long history in statistical data analysis, with many impactful applications. However, in many modern machine learning settings, the benefits of ensembling are less ubiquitous and less obvious. We study, both theoretically and empirically, the fundamental question of when ensembling yields significant performance improvements in classification tasks. Theoretically, we prove new results relating the \emph{ensemble improvement rate} (a measure of how much ensembling decreases the error rate versus a single model, on a relative scale) to the \emph{disagreement-error ratio}. We show that ensembling improves performance significantly whenever the disagreement rate is large relative to the average error rate; and that, conversely, one classifier is often enough whenever the disagreement rate is low relative to the average error rate. On the way to proving these results, we derive, under a mild condition called \emph{competence}, improved upper and lower bounds on the average test error rate of the majority vote classifier. To complement this theory, we study ensembling empirically in a variety of settings, verifying the predictions made by our theory, and identifying practical scenarios where ensembling does and does not result in large performance improvements. Perhaps most notably, we demonstrate a distinct difference in behavior between interpolating models (popular in current practice) and non-interpolating models (such as tree-based methods, where ensembling is popular), demonstrating that ensembling helps considerably more in the latter case than in the former.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge