KCES: Training-Free Defense for Robust Graph Neural Networks via Kernel Complexity

Graph Neural Networks (GNNs) have achieved impressive success across a wide range of graph-based tasks, yet they remain highly vulnerable to small, imperceptible perturbations and adversarial attacks. Although numerous defense methods have been proposed to address these vulnerabilities, many rely on heuristic metrics, overfit to specific attack patterns, and suffer from high computational complexity. In this paper, we propose Kernel Complexity-Based Edge Sanitization (KCES), a training-free, model-agnostic defense framework. KCES leverages Graph Kernel Complexity (GKC), a novel metric derived from the graph's Gram matrix that characterizes GNN generalization via its test error bound. Building on GKC, we define a KC score for each edge, measuring the change in GKC when the edge is removed. Edges with high KC scores, typically introduced by adversarial perturbations, are pruned to mitigate their harmful effects, thereby enhancing GNNs' robustness. KCES can also be seamlessly integrated with existing defense strategies as a plug-and-play module without requiring training. Theoretical analysis and extensive experiments demonstrate that KCES consistently enhances GNN robustness, outperforms state-of-the-art baselines, and amplifies the effectiveness of existing defenses, offering a principled and efficient solution for securing GNNs.

Eigenspectrum Analysis of Neural Networks without Aspect Ratio Bias

Diagnosing deep neural networks (DNNs) through the eigenspectrum of weight matrices has been an active area of research in recent years. At a high level, eigenspectrum analysis of DNNs involves measuring the heavytailness of the empirical spectral densities (ESD) of weight matrices. It provides insight into how well a model is trained and can guide decisions on assigning better layer-wise training hyperparameters. In this paper, we address a challenge associated with such eigenspectrum methods: the impact of the aspect ratio of weight matrices on estimated heavytailness metrics. We demonstrate that matrices of varying sizes (and aspect ratios) introduce a non-negligible bias in estimating heavytailness metrics, leading to inaccurate model diagnosis and layer-wise hyperparameter assignment. To overcome this challenge, we propose FARMS (Fixed-Aspect-Ratio Matrix Subsampling), a method that normalizes the weight matrices by subsampling submatrices with a fixed aspect ratio. Instead of measuring the heavytailness of the original ESD, we measure the average ESD of these subsampled submatrices. We show that measuring the heavytailness of these submatrices with the fixed aspect ratio can effectively mitigate the aspect ratio bias. We validate our approach across various optimization techniques and application domains that involve eigenspectrum analysis of weights, including image classification in computer vision (CV) models, scientific machine learning (SciML) model training, and large language model (LLM) pruning. Our results show that despite its simplicity, FARMS uniformly improves the accuracy of eigenspectrum analysis while enabling more effective layer-wise hyperparameter assignment in these application domains. In one of the LLM pruning experiments, FARMS reduces the perplexity of the LLaMA-7B model by 17.3% when compared with the state-of-the-art method.

Why LLM Safety Guardrails Collapse After Fine-tuning: A Similarity Analysis Between Alignment and Fine-tuning Datasets

Recent advancements in large language models (LLMs) have underscored their vulnerability to safety alignment jailbreaks, particularly when subjected to downstream fine-tuning. However, existing mitigation strategies primarily focus on reactively addressing jailbreak incidents after safety guardrails have been compromised, removing harmful gradients during fine-tuning, or continuously reinforcing safety alignment throughout fine-tuning. As such, they tend to overlook a critical upstream factor: the role of the original safety-alignment data. This paper therefore investigates the degradation of safety guardrails through the lens of representation similarity between upstream alignment datasets and downstream fine-tuning tasks. Our experiments demonstrate that high similarity between these datasets significantly weakens safety guardrails, making models more susceptible to jailbreaks. Conversely, low similarity between these two types of datasets yields substantially more robust models and thus reduces harmfulness score by up to 10.33%. By highlighting the importance of upstream dataset design in the building of durable safety guardrails and reducing real-world vulnerability to jailbreak attacks, these findings offer actionable insights for fine-tuning service providers.

A Model Zoo on Phase Transitions in Neural Networks

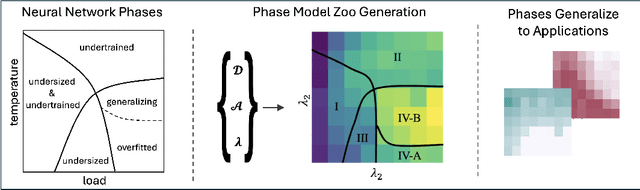
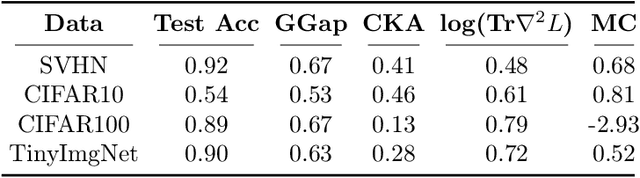
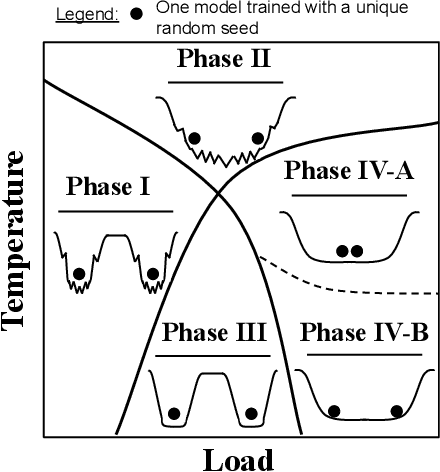
Using the weights of trained Neural Network (NN) models as data modality has recently gained traction as a research field - dubbed Weight Space Learning (WSL). Multiple recent works propose WSL methods to analyze models, evaluate methods, or synthesize weights. Weight space learning methods require populations of trained models as datasets for development and evaluation. However, existing collections of models - called `model zoos' - are unstructured or follow a rudimentary definition of diversity. In parallel, work rooted in statistical physics has identified phases and phase transitions in NN models. Models are homogeneous within the same phase but qualitatively differ from one phase to another. We combine the idea of `model zoos' with phase information to create a controlled notion of diversity in populations. We introduce 12 large-scale zoos that systematically cover known phases and vary over model architecture, size, and datasets. These datasets cover different modalities, such as computer vision, natural language processing, and scientific ML. For every model, we compute loss landscape metrics and validate full coverage of the phases. With this dataset, we provide the community with a resource with a wide range of potential applications for WSL and beyond. Evidence suggests the loss landscape phase plays a role in applications such as model training, analysis, or sparsification. We demonstrate this in an exploratory study of the downstream methods like transfer learning or model weights averaging.

LossLens: Diagnostics for Machine Learning through Loss Landscape Visual Analytics

Modern machine learning often relies on optimizing a neural network's parameters using a loss function to learn complex features. Beyond training, examining the loss function with respect to a network's parameters (i.e., as a loss landscape) can reveal insights into the architecture and learning process. While the local structure of the loss landscape surrounding an individual solution can be characterized using a variety of approaches, the global structure of a loss landscape, which includes potentially many local minima corresponding to different solutions, remains far more difficult to conceptualize and visualize. To address this difficulty, we introduce LossLens, a visual analytics framework that explores loss landscapes at multiple scales. LossLens integrates metrics from global and local scales into a comprehensive visual representation, enhancing model diagnostics. We demonstrate LossLens through two case studies: visualizing how residual connections influence a ResNet-20, and visualizing how physical parameters influence a physics-informed neural network (PINN) solving a simple convection problem.

Visualizing Loss Functions as Topological Landscape Profiles

In machine learning, a loss function measures the difference between model predictions and ground-truth (or target) values. For neural network models, visualizing how this loss changes as model parameters are varied can provide insights into the local structure of the so-called loss landscape (e.g., smoothness) as well as global properties of the underlying model (e.g., generalization performance). While various methods for visualizing the loss landscape have been proposed, many approaches limit sampling to just one or two directions, ignoring potentially relevant information in this extremely high-dimensional space. This paper introduces a new representation based on topological data analysis that enables the visualization of higher-dimensional loss landscapes. After describing this new topological landscape profile representation, we show how the shape of loss landscapes can reveal new details about model performance and learning dynamics, highlighting several use cases, including image segmentation (e.g., UNet) and scientific machine learning (e.g., physics-informed neural networks). Through these examples, we provide new insights into how loss landscapes vary across distinct hyperparameter spaces: we find that the topology of the loss landscape is simpler for better-performing models; and we observe greater variation in the shape of loss landscapes near transitions from low to high model performance.

Evaluating Loss Landscapes from a Topology Perspective

Characterizing the loss of a neural network with respect to model parameters, i.e., the loss landscape, can provide valuable insights into properties of that model. Various methods for visualizing loss landscapes have been proposed, but less emphasis has been placed on quantifying and extracting actionable and reproducible insights from these complex representations. Inspired by powerful tools from topological data analysis (TDA) for summarizing the structure of high-dimensional data, here we characterize the underlying shape (or topology) of loss landscapes, quantifying the topology to reveal new insights about neural networks. To relate our findings to the machine learning (ML) literature, we compute simple performance metrics (e.g., accuracy, error), and we characterize the local structure of loss landscapes using Hessian-based metrics (e.g., largest eigenvalue, trace, eigenvalue spectral density). Following this approach, we study established models from image pattern recognition (e.g., ResNets) and scientific ML (e.g., physics-informed neural networks), and we show how quantifying the shape of loss landscapes can provide new insights into model performance and learning dynamics.

Model Balancing Helps Low-data Training and Fine-tuning

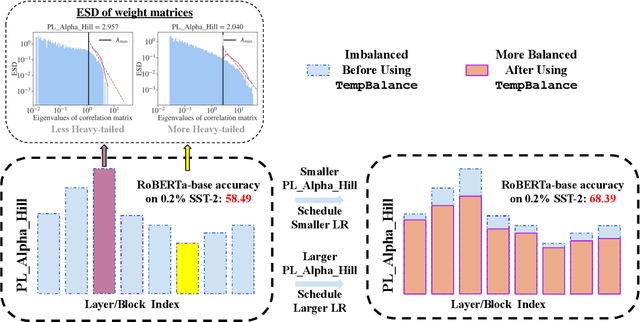
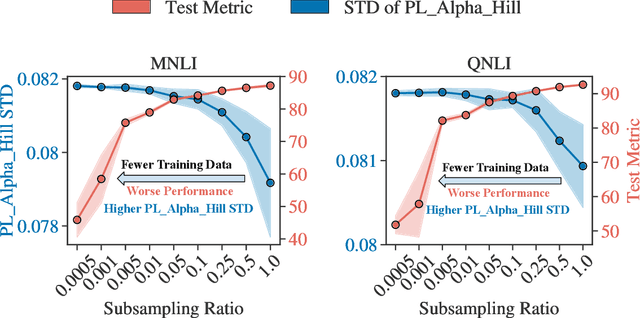
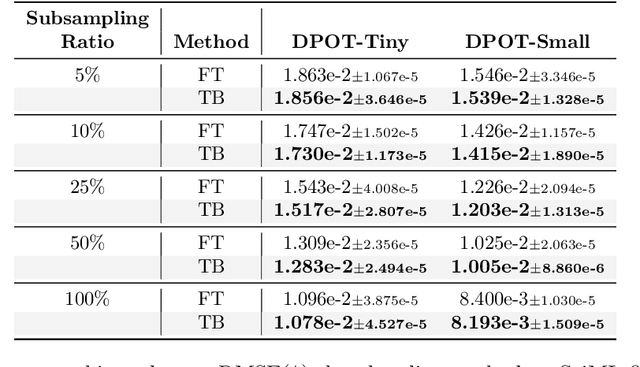
Recent advances in foundation models have emphasized the need to align pre-trained models with specialized domains using small, curated datasets. Studies on these foundation models underscore the importance of low-data training and fine-tuning. This topic, well-known in natural language processing (NLP), has also gained increasing attention in the emerging field of scientific machine learning (SciML). To address the limitations of low-data training and fine-tuning, we draw inspiration from Heavy-Tailed Self-Regularization (HT-SR) theory, analyzing the shape of empirical spectral densities (ESDs) and revealing an imbalance in training quality across different model layers. To mitigate this issue, we adapt a recently proposed layer-wise learning rate scheduler, TempBalance, which effectively balances training quality across layers and enhances low-data training and fine-tuning for both NLP and SciML tasks. Notably, TempBalance demonstrates increasing performance gains as the amount of available tuning data decreases. Comparative analyses further highlight the effectiveness of TempBalance and its adaptability as an "add-on" method for improving model performance.

AlphaLoRA: Assigning LoRA Experts Based on Layer Training Quality

Parameter-efficient fine-tuning methods, such as Low-Rank Adaptation (LoRA), are known to enhance training efficiency in Large Language Models (LLMs). Due to the limited parameters of LoRA, recent studies seek to combine LoRA with Mixture-of-Experts (MoE) to boost performance across various tasks. However, inspired by the observed redundancy in traditional MoE structures, previous studies identify similar redundancy among LoRA experts within the MoE architecture, highlighting the necessity for non-uniform allocation of LoRA experts across different layers. In this paper, we leverage Heavy-Tailed Self-Regularization (HT-SR) Theory to design a fine-grained allocation strategy. Our analysis reveals that the number of experts per layer correlates with layer training quality, which exhibits significant variability across layers. Based on this, we introduce AlphaLoRA, a theoretically principled and training-free method for allocating LoRA experts to further mitigate redundancy. Experiments on three models across ten language processing and reasoning benchmarks demonstrate that AlphaLoRA achieves comparable or superior performance over all baselines. Our code is available at https://github.com/morelife2017/alphalora.

AlphaPruning: Using Heavy-Tailed Self Regularization Theory for Improved Layer-wise Pruning of Large Language Models

Recent work on pruning large language models (LLMs) has shown that one can eliminate a large number of parameters without compromising performance, making pruning a promising strategy to reduce LLM model size. Existing LLM pruning strategies typically assign uniform pruning ratios across layers, limiting overall pruning ability; and recent work on layerwise pruning of LLMs is often based on heuristics that can easily lead to suboptimal performance. In this paper, we leverage Heavy-Tailed Self-Regularization (HT-SR) Theory, in particular the shape of empirical spectral densities (ESDs) of weight matrices, to design improved layerwise pruning ratios for LLMs. Our analysis reveals a wide variability in how well-trained, and thus relatedly how prunable, different layers of an LLM are. Based on this, we propose AlphaPruning, which uses shape metrics to allocate layerwise sparsity ratios in a more theoretically principled manner. AlphaPruning can be used in conjunction with multiple existing LLM pruning methods. Our empirical results show that AlphaPruning prunes LLaMA-7B to 80% sparsity while maintaining reasonable perplexity, marking a first in the literature on LLMs. We have open-sourced our code at https://github.com/haiquanlu/AlphaPruning.