Learning Model Representations Using Publicly Available Model Hubs

The weights of neural networks have emerged as a novel data modality, giving rise to the field of weight space learning. A central challenge in this area is that learning meaningful representations of weights typically requires large, carefully constructed collections of trained models, typically referred to as model zoos. These model zoos are often trained ad-hoc, requiring large computational resources, constraining the learned weight space representations in scale and flexibility. In this work, we drop this requirement by training a weight space learning backbone on arbitrary models downloaded from large, unstructured model repositories such as Hugging Face. Unlike curated model zoos, these repositories contain highly heterogeneous models: they vary in architecture and dataset, and are largely undocumented. To address the methodological challenges posed by such heterogeneity, we propose a new weight space backbone designed to handle unstructured model populations. We demonstrate that weight space representations trained on models from Hugging Face achieve strong performance, often outperforming backbones trained on laboratory-generated model zoos. Finally, we show that the diversity of the model weights in our training set allows our weight space model to generalize to unseen data modalities. By demonstrating that high-quality weight space representations can be learned in the wild, we show that curated model zoos are not indispensable, thereby overcoming a strong limitation currently faced by the weight space learning community.

A Model Zoo on Phase Transitions in Neural Networks

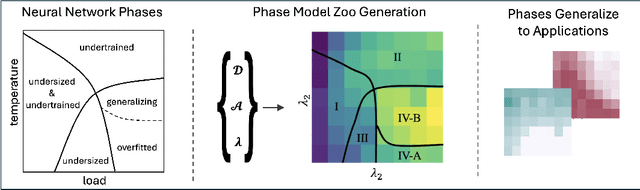
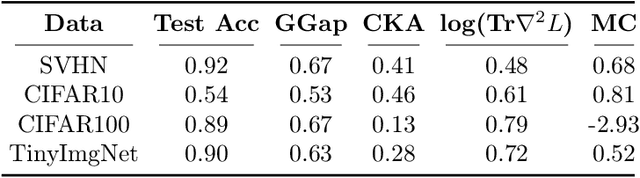
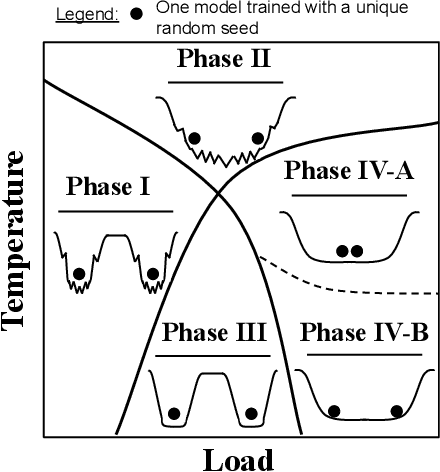
Using the weights of trained Neural Network (NN) models as data modality has recently gained traction as a research field - dubbed Weight Space Learning (WSL). Multiple recent works propose WSL methods to analyze models, evaluate methods, or synthesize weights. Weight space learning methods require populations of trained models as datasets for development and evaluation. However, existing collections of models - called `model zoos' - are unstructured or follow a rudimentary definition of diversity. In parallel, work rooted in statistical physics has identified phases and phase transitions in NN models. Models are homogeneous within the same phase but qualitatively differ from one phase to another. We combine the idea of `model zoos' with phase information to create a controlled notion of diversity in populations. We introduce 12 large-scale zoos that systematically cover known phases and vary over model architecture, size, and datasets. These datasets cover different modalities, such as computer vision, natural language processing, and scientific ML. For every model, we compute loss landscape metrics and validate full coverage of the phases. With this dataset, we provide the community with a resource with a wide range of potential applications for WSL and beyond. Evidence suggests the loss landscape phase plays a role in applications such as model training, analysis, or sparsification. We demonstrate this in an exploratory study of the downstream methods like transfer learning or model weights averaging.

The Impact of Model Zoo Size and Composition on Weight Space Learning

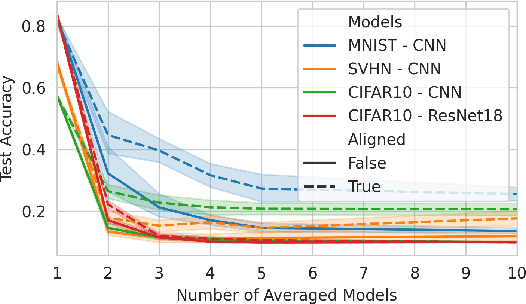
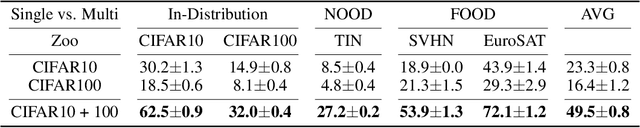
Re-using trained neural network models is a common strategy to reduce training cost and transfer knowledge. Weight space learning - using the weights of trained models as data modality - is a promising new field to re-use populations of pre-trained models for future tasks. Approaches in this field have demonstrated high performance both on model analysis and weight generation tasks. However, until now their learning setup requires homogeneous model zoos where all models share the same exact architecture, limiting their capability to generalize beyond the population of models they saw during training. In this work, we remove this constraint and propose a modification to a common weight space learning method to accommodate training on heterogeneous populations of models. We further investigate the resulting impact of model diversity on generating unseen neural network model weights for zero-shot knowledge transfer. Our extensive experimental evaluation shows that including models with varying underlying image datasets has a high impact on performance and generalization, for both in- and out-of-distribution settings. Code is available on github.com/HSG-AIML/MultiZoo-SANE.

A Model Zoo of Vision Transformers

The availability of large, structured populations of neural networks - called 'model zoos' - has led to the development of a multitude of downstream tasks ranging from model analysis, to representation learning on model weights or generative modeling of neural network parameters. However, existing model zoos are limited in size and architecture and neglect the transformer, which is among the currently most successful neural network architectures. We address this gap by introducing the first model zoo of vision transformers (ViT). To better represent recent training approaches, we develop a new blueprint for model zoo generation that encompasses both pre-training and fine-tuning steps, and publish 250 unique models. They are carefully generated with a large span of generating factors, and their diversity is validated using a thorough choice of weight-space and behavioral metrics. To further motivate the utility of our proposed dataset, we suggest multiple possible applications grounded in both extensive exploratory experiments and a number of examples from the existing literature. By extending previous lines of similar work, our model zoo allows researchers to push their model population-based methods from the small model regime to state-of-the-art architectures. We make our model zoo available at github.com/ModelZoos/ViTModelZoo.

Structure Is Not Enough: Leveraging Behavior for Neural Network Weight Reconstruction

The weights of neural networks (NNs) have recently gained prominence as a new data modality in machine learning, with applications ranging from accuracy and hyperparameter prediction to representation learning or weight generation. One approach to leverage NN weights involves training autoencoders (AEs), using contrastive and reconstruction losses. This allows such models to be applied to a wide variety of downstream tasks, and they demonstrate strong predictive performance and low reconstruction error. However, despite the low reconstruction error, these AEs reconstruct NN models with deteriorated performance compared to the original ones, limiting their usability with regard to model weight generation. In this paper, we identify a limitation of weight-space AEs, specifically highlighting that a structural loss, that uses the Euclidean distance between original and reconstructed weights, fails to capture some features critical for reconstructing high-performing models. We analyze the addition of a behavioral loss for training AEs in weight space, where we compare the output of the reconstructed model with that of the original one, given some common input. We show a strong synergy between structural and behavioral signals, leading to increased performance in all downstream tasks evaluated, in particular NN weights reconstruction and generation.

Hyper-Representations: Learning from Populations of Neural Networks

This thesis addresses the challenge of understanding Neural Networks through the lens of their most fundamental component: the weights, which encapsulate the learned information and determine the model behavior. At the core of this thesis is a fundamental question: Can we learn general, task-agnostic representations from populations of Neural Network models? The key contribution of this thesis to answer that question are hyper-representations, a self-supervised method to learn representations of NN weights. Work in this thesis finds that trained NN models indeed occupy meaningful structures in the weight space, that can be learned and used. Through extensive experiments, this thesis demonstrates that hyper-representations uncover model properties, such as their performance, state of training, or hyperparameters. Moreover, the identification of regions with specific properties in hyper-representation space allows to sample and generate model weights with targeted properties. This thesis demonstrates applications for fine-tuning, and transfer learning to great success. Lastly, it presents methods that allow hyper-representations to generalize beyond model sizes, architectures, and tasks. The practical implications of that are profound, as it opens the door to foundation models of Neural Networks, which aggregate and instantiate their knowledge across models and architectures. Ultimately, this thesis contributes to the deeper understanding of Neural Networks by investigating structures in their weights which leads to more interpretable, efficient, and adaptable models. By laying the groundwork for representation learning of NN weights, this research demonstrates the potential to change the way Neural Networks are developed, analyzed, and used.

Dirac--Bianconi Graph Neural Networks -- Enabling Non-Diffusive Long-Range Graph Predictions

The geometry of a graph is encoded in dynamical processes on the graph. Many graph neural network (GNN) architectures are inspired by such dynamical systems, typically based on the graph Laplacian. Here, we introduce Dirac--Bianconi GNNs (DBGNNs), which are based on the topological Dirac equation recently proposed by Bianconi. Based on the graph Laplacian, we demonstrate that DBGNNs explore the geometry of the graph in a fundamentally different way than conventional message passing neural networks (MPNNs). While regular MPNNs propagate features diffusively, analogous to the heat equation, DBGNNs allow for coherent long-range propagation. Experimental results showcase the superior performance of DBGNNs over existing conventional MPNNs for long-range predictions of power grid stability and peptide properties. This study highlights the effectiveness of DBGNNs in capturing intricate graph dynamics, providing notable advancements in GNN architectures.

MD tree: a model-diagnostic tree grown on loss landscape

This paper considers "model diagnosis", which we formulate as a classification problem. Given a pre-trained neural network (NN), the goal is to predict the source of failure from a set of failure modes (such as a wrong hyperparameter, inadequate model size, and insufficient data) without knowing the training configuration of the pre-trained NN. The conventional diagnosis approach uses training and validation errors to determine whether the model is underfitting or overfitting. However, we show that rich information about NN performance is encoded in the optimization loss landscape, which provides more actionable insights than validation-based measurements. Therefore, we propose a diagnosis method called MD tree based on loss landscape metrics and experimentally demonstrate its advantage over classical validation-based approaches. We verify the effectiveness of MD tree in multiple practical scenarios: (1) use several models trained on one dataset to diagnose a model trained on another dataset, essentially a few-shot dataset transfer problem; (2) use small models (or models trained with small data) to diagnose big models (or models trained with big data), essentially a scale transfer problem. In a dataset transfer task, MD tree achieves an accuracy of 87.7%, outperforming validation-based approaches by 14.88%. Our code is available at https://github.com/YefanZhou/ModelDiagnosis.

Towards Scalable and Versatile Weight Space Learning

Learning representations of well-trained neural network models holds the promise to provide an understanding of the inner workings of those models. However, previous work has either faced limitations when processing larger networks or was task-specific to either discriminative or generative tasks. This paper introduces the SANE approach to weight-space learning. SANE overcomes previous limitations by learning task-agnostic representations of neural networks that are scalable to larger models of varying architectures and that show capabilities beyond a single task. Our method extends the idea of hyper-representations towards sequential processing of subsets of neural network weights, thus allowing one to embed larger neural networks as a set of tokens into the learned representation space. SANE reveals global model information from layer-wise embeddings, and it can sequentially generate unseen neural network models, which was unattainable with previous hyper-representation learning methods. Extensive empirical evaluation demonstrates that SANE matches or exceeds state-of-the-art performance on several weight representation learning benchmarks, particularly in initialization for new tasks and larger ResNet architectures.

Sparsified Model Zoo Twins: Investigating Populations of Sparsified Neural Network Models

With growing size of Neural Networks (NNs), model sparsification to reduce the computational cost and memory demand for model inference has become of vital interest for both research and production. While many sparsification methods have been proposed and successfully applied on individual models, to the best of our knowledge their behavior and robustness has not yet been studied on large populations of models. With this paper, we address that gap by applying two popular sparsification methods on populations of models (so called model zoos) to create sparsified versions of the original zoos. We investigate the performance of these two methods for each zoo, compare sparsification layer-wise, and analyse agreement between original and sparsified populations. We find both methods to be very robust with magnitude pruning able outperform variational dropout with the exception of high sparsification ratios above 80%. Further, we find sparsified models agree to a high degree with their original non-sparsified counterpart, and that the performance of original and sparsified model is highly correlated. Finally, all models of the model zoos and their sparsified model twins are publicly available: modelzoos.cc.