Pathwise Gradient Variance Reduction with Control Variates in Variational Inference

Variational inference in Bayesian deep learning often involves computing the gradient of an expectation that lacks a closed-form solution. In these cases, pathwise and score-function gradient estimators are the most common approaches. The pathwise estimator is often favoured for its substantially lower variance compared to the score-function estimator, which typically requires variance reduction techniques. However, recent research suggests that even pathwise gradient estimators could benefit from variance reduction. In this work, we review existing control-variates-based variance reduction methods for pathwise gradient estimators to assess their effectiveness. Notably, these methods often rely on integrand approximations and are applicable only to simple variational families. To address this limitation, we propose applying zero-variance control variates to pathwise gradient estimators. This approach offers the advantage of requiring minimal assumptions about the variational distribution, other than being able to sample from it.

Temperature Optimization for Bayesian Deep Learning

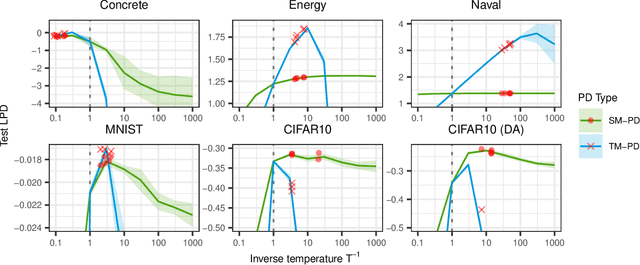
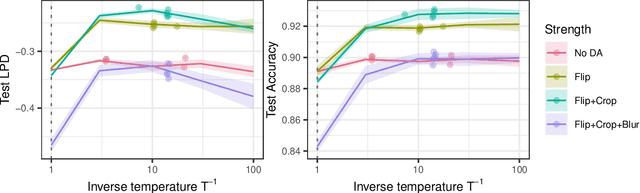
The Cold Posterior Effect (CPE) is a phenomenon in Bayesian Deep Learning (BDL), where tempering the posterior to a cold temperature often improves the predictive performance of the posterior predictive distribution (PPD). Although the term `CPE' suggests colder temperatures are inherently better, the BDL community increasingly recognizes that this is not always the case. Despite this, there remains no systematic method for finding the optimal temperature beyond grid search. In this work, we propose a data-driven approach to select the temperature that maximizes test log-predictive density, treating the temperature as a model parameter and estimating it directly from the data. We empirically demonstrate that our method performs comparably to grid search, at a fraction of the cost, across both regression and classification tasks. Finally, we highlight the differing perspectives on CPE between the BDL and Generalized Bayes communities: while the former primarily focuses on predictive performance of the PPD, the latter emphasizes calibrated uncertainty and robustness to model misspecification; these distinct objectives lead to different temperature preferences.