Spectral Estimation with Free Decompression

Computing eigenvalues of very large matrices is a critical task in many machine learning applications, including the evaluation of log-determinants, the trace of matrix functions, and other important metrics. As datasets continue to grow in scale, the corresponding covariance and kernel matrices become increasingly large, often reaching magnitudes that make their direct formation impractical or impossible. Existing techniques typically rely on matrix-vector products, which can provide efficient approximations, if the matrix spectrum behaves well. However, in settings like distributed learning, or when the matrix is defined only indirectly, access to the full data set can be restricted to only very small sub-matrices of the original matrix. In these cases, the matrix of nominal interest is not even available as an implicit operator, meaning that even matrix-vector products may not be available. In such settings, the matrix is "impalpable," in the sense that we have access to only masked snapshots of it. We draw on principles from free probability theory to introduce a novel method of "free decompression" to estimate the spectrum of such matrices. Our method can be used to extrapolate from the empirical spectral densities of small submatrices to infer the eigenspectrum of extremely large (impalpable) matrices (that we cannot form or even evaluate with full matrix-vector products). We demonstrate the effectiveness of this approach through a series of examples, comparing its performance against known limiting distributions from random matrix theory in synthetic settings, as well as applying it to submatrices of real-world datasets, matching them with their full empirical eigenspectra.

Determinant Estimation under Memory Constraints and Neural Scaling Laws

Calculating or accurately estimating log-determinants of large positive semi-definite matrices is of fundamental importance in many machine learning tasks. While its cubic computational complexity can already be prohibitive, in modern applications, even storing the matrices themselves can pose a memory bottleneck. To address this, we derive a novel hierarchical algorithm based on block-wise computation of the LDL decomposition for large-scale log-determinant calculation in memory-constrained settings. In extreme cases where matrices are highly ill-conditioned, accurately computing the full matrix itself may be infeasible. This is particularly relevant when considering kernel matrices at scale, including the empirical Neural Tangent Kernel (NTK) of neural networks trained on large datasets. Under the assumption of neural scaling laws in the test error, we show that the ratio of pseudo-determinants satisfies a power-law relationship, allowing us to derive corresponding scaling laws. This enables accurate estimation of NTK log-determinants from a tiny fraction of the full dataset; in our experiments, this results in a $\sim$100,000$\times$ speedup with improved accuracy over competing approximations. Using these techniques, we successfully estimate log-determinants for dense matrices of extreme sizes, which were previously deemed intractable and inaccessible due to their enormous scale and computational demands.

A Statistical Framework for Ranking LLM-Based Chatbots

Large language models (LLMs) have transformed natural language processing, with frameworks like Chatbot Arena providing pioneering platforms for evaluating these models. By facilitating millions of pairwise comparisons based on human judgments, Chatbot Arena has become a cornerstone in LLM evaluation, offering rich datasets for ranking models in open-ended conversational tasks. Building upon this foundation, we propose a statistical framework that incorporates key advancements to address specific challenges in pairwise comparison analysis. First, we introduce a factored tie model that enhances the ability to handle ties -- an integral aspect of human-judged comparisons -- significantly improving the model's fit to observed data. Second, we extend the framework to model covariance between competitors, enabling deeper insights into performance relationships and facilitating intuitive groupings into performance tiers. Third, we resolve optimization challenges arising from parameter non-uniqueness by introducing novel constraints, ensuring stable and interpretable parameter estimation. Through rigorous evaluation and extensive experimentation, our framework demonstrates substantial improvements over existing methods in modeling pairwise comparison data. To support reproducibility and practical adoption, we release leaderbot, an open-source Python package implementing our models and analyses.

A Singular Woodbury and Pseudo-Determinant Matrix Identities and Application to Gaussian Process Regression

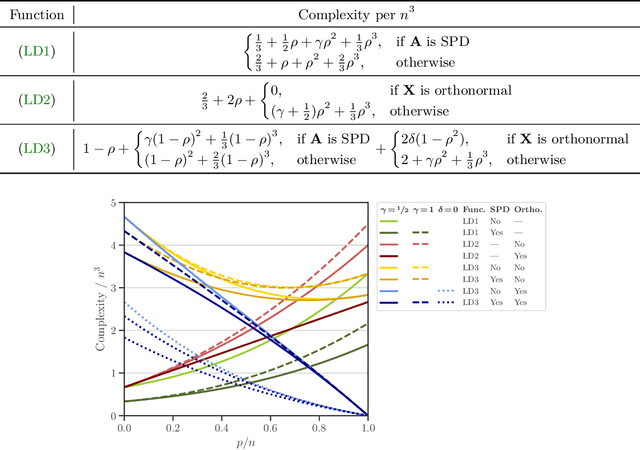
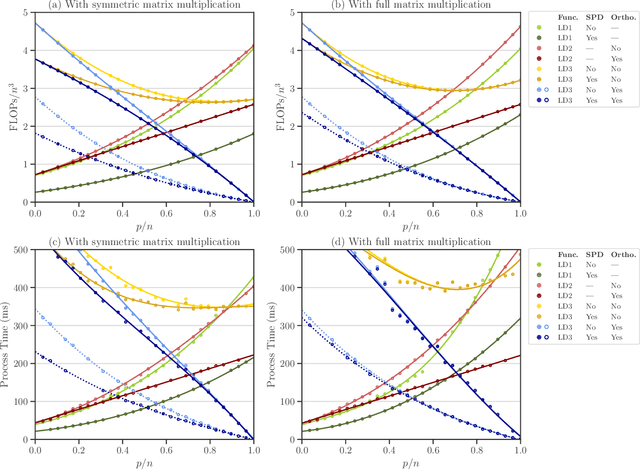
We study a matrix that arises in a singular formulation of the Woodbury matrix identity when the Woodbury identity no longer holds. We present generalized inverse and pseudo-determinant identities for such matrix that have direct applications to the Gaussian process regression, in particular, its likelihood representation and its precision matrix. We also provide an efficient algorithm and numerical analysis for the presented determinant identities and demonstrate their advantages in certain conditions which are applicable to computing log-determinant terms in likelihood functions of Gaussian process regression.

Noise Estimation in Gaussian Process Regression

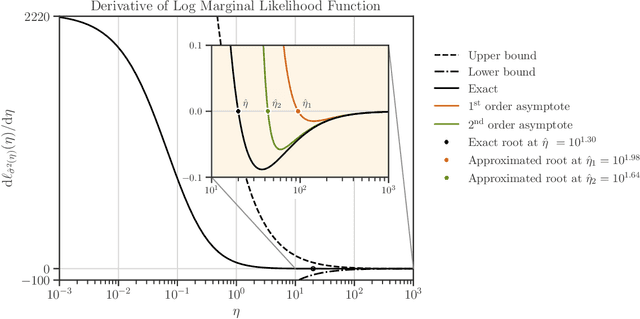
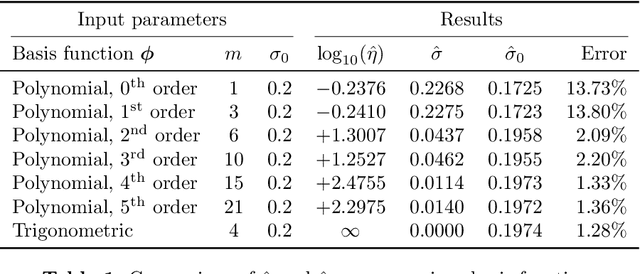
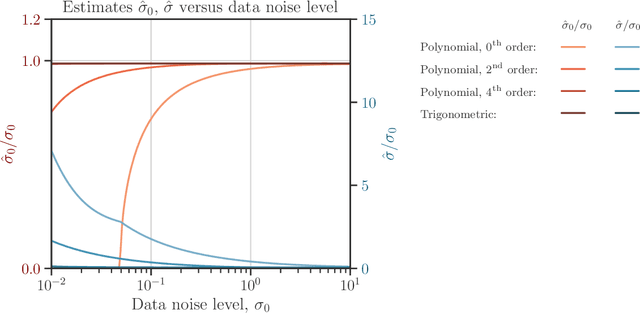
We develop a computational procedure to estimate the covariance hyperparameters for semiparametric Gaussian process regression models with additive noise. Namely, the presented method can be used to efficiently estimate the variance of the correlated error, and the variance of the noise based on maximizing a marginal likelihood function. Our method involves suitably reducing the dimensionality of the hyperparameter space to simplify the estimation procedure to a univariate root-finding problem. Moreover, we derive bounds and asymptotes of the marginal likelihood function and its derivatives, which are useful to narrowing the initial range of the hyperparameter search. Using numerical examples, we demonstrate the computational advantages and robustness of the presented approach compared to traditional parameter optimization.

Interpolating the Trace of the Inverse of Matrix $\mathbf{A} + t \mathbf{B}$

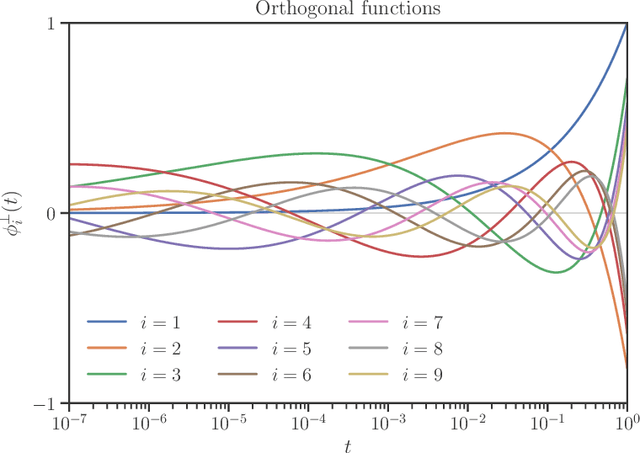
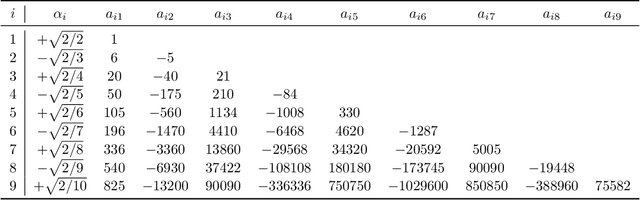
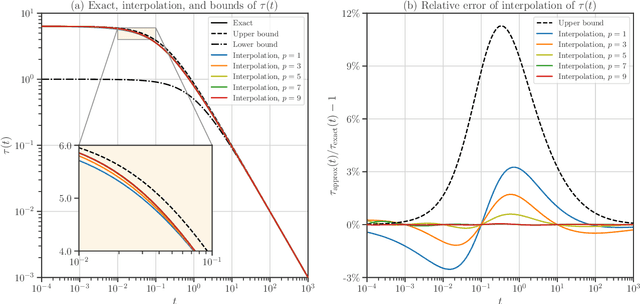
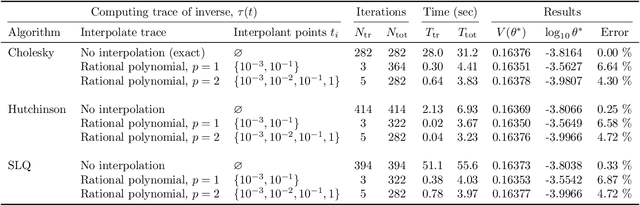
We develop heuristic interpolation methods for the function $t \mapsto \operatorname{trace}\left( (\mathbf{A} + t \mathbf{B})^{-1} \right)$, where the matrices $\mathbf{A}$ and $\mathbf{B}$ are symmetric and positive definite and $t$ is a real variable. This function is featured in many applications in statistics, machine learning, and computational physics. The presented interpolation functions are based on the modification of a sharp upper bound that we derive for this function, which is a new trace inequality for matrices. We demonstrate the accuracy and performance of the proposed method with numerical examples, namely, the marginal maximum likelihood estimation for linear Gaussian process regression and the estimation of the regularization parameter of ridge regression with the generalized cross-validation method.