A Singular Woodbury and Pseudo-Determinant Matrix Identities and Application to Gaussian Process Regression

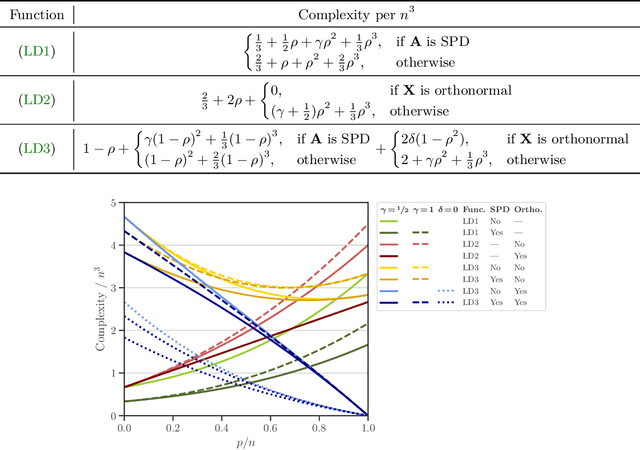
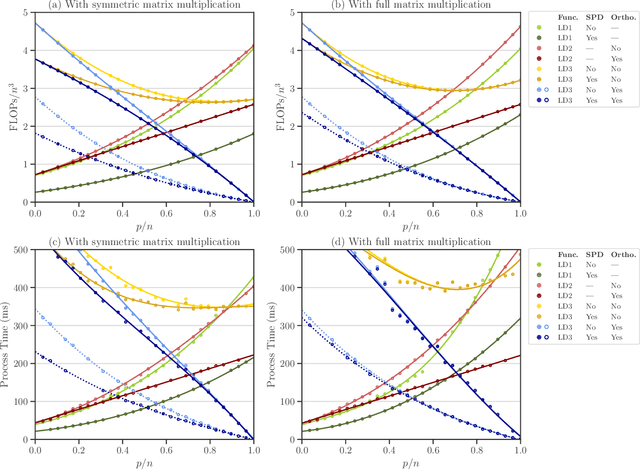
We study a matrix that arises in a singular formulation of the Woodbury matrix identity when the Woodbury identity no longer holds. We present generalized inverse and pseudo-determinant identities for such matrix that have direct applications to the Gaussian process regression, in particular, its likelihood representation and its precision matrix. We also provide an efficient algorithm and numerical analysis for the presented determinant identities and demonstrate their advantages in certain conditions which are applicable to computing log-determinant terms in likelihood functions of Gaussian process regression.

Noise Estimation in Gaussian Process Regression

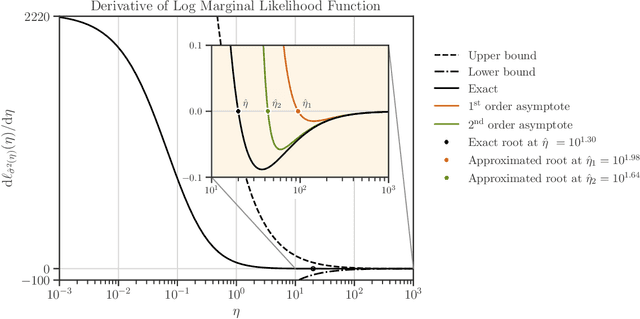
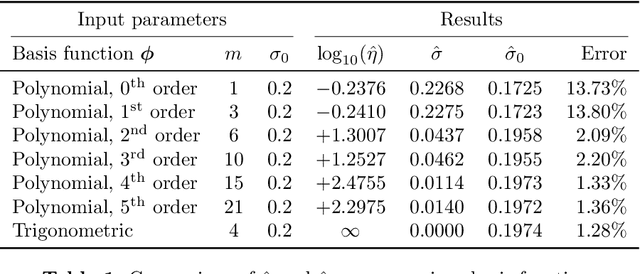
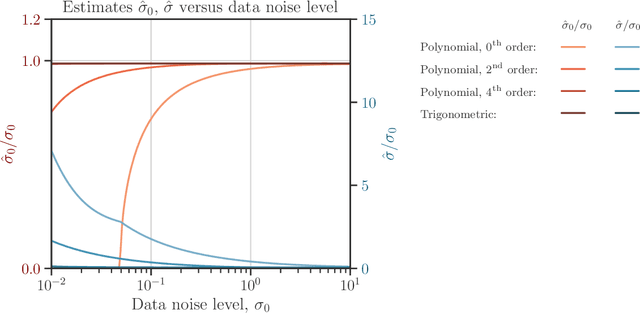
We develop a computational procedure to estimate the covariance hyperparameters for semiparametric Gaussian process regression models with additive noise. Namely, the presented method can be used to efficiently estimate the variance of the correlated error, and the variance of the noise based on maximizing a marginal likelihood function. Our method involves suitably reducing the dimensionality of the hyperparameter space to simplify the estimation procedure to a univariate root-finding problem. Moreover, we derive bounds and asymptotes of the marginal likelihood function and its derivatives, which are useful to narrowing the initial range of the hyperparameter search. Using numerical examples, we demonstrate the computational advantages and robustness of the presented approach compared to traditional parameter optimization.

Whole Heart Mesh Generation For Image-Based Computational Simulations By Learning Free-From Deformations

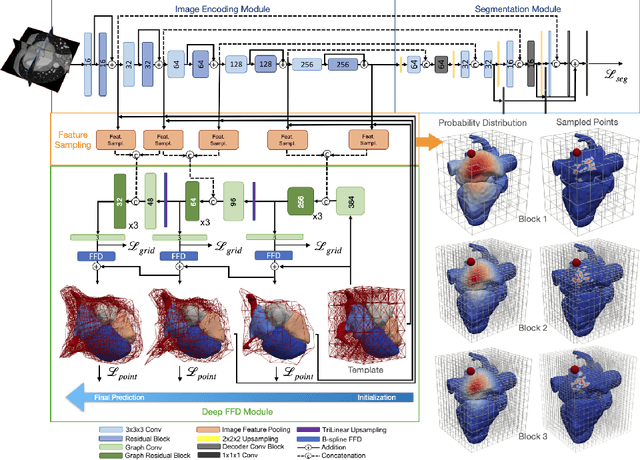
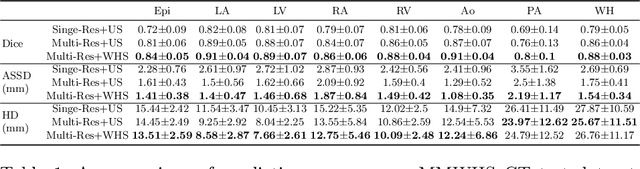
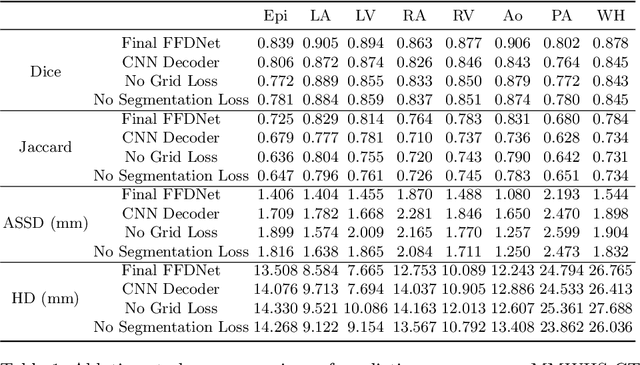
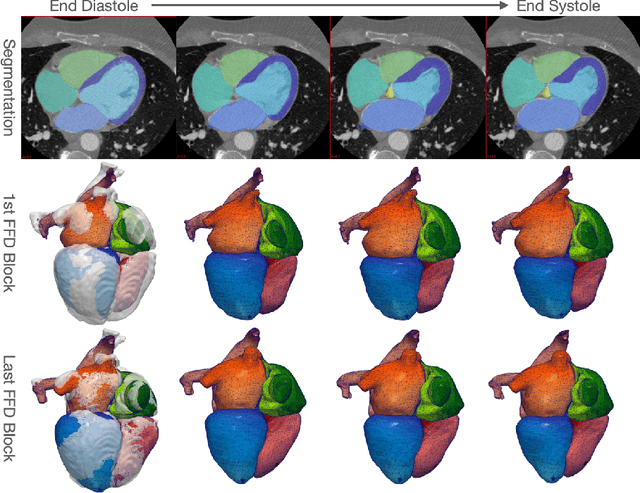
Image-based computer simulation of cardiac function can be used to probe the mechanisms of (patho)physiology, and guide diagnosis and personalized treatment of cardiac diseases. This paradigm requires constructing simulation-ready meshes of cardiac structures from medical image data--a process that has traditionally required significant time and human effort, limiting large-cohort analyses and potential clinical translations. We propose a novel deep learning approach to reconstruct simulation-ready whole heart meshes from volumetric image data. Our approach learns to deform a template mesh to the input image data by predicting displacements of multi-resolution control point grids. We discuss the methods of this approach and demonstrate its application to efficiently create simulation-ready whole heart meshes for computational fluid dynamics simulations of the cardiac flow. Our source code is available at https://github.com/fkong7/HeartFFDNet.

A Deep-Learning Approach For Direct Whole-Heart Mesh Reconstruction

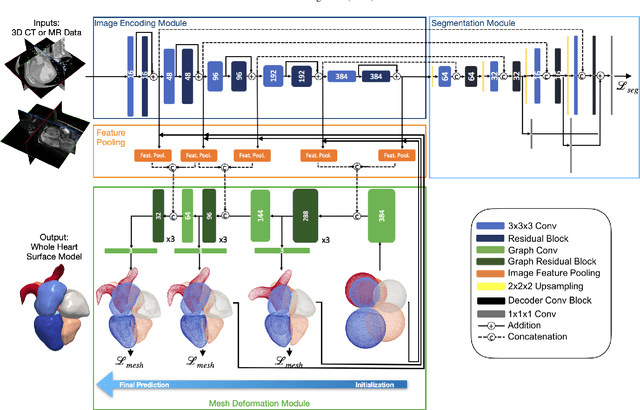
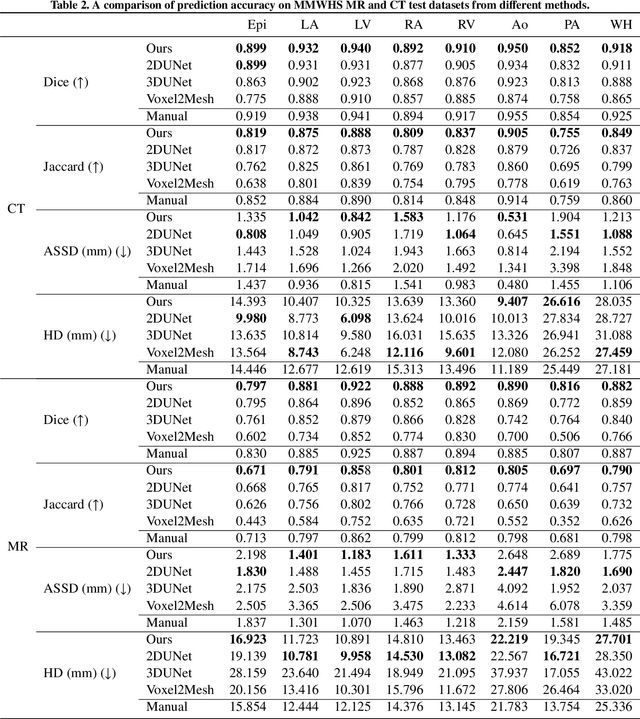
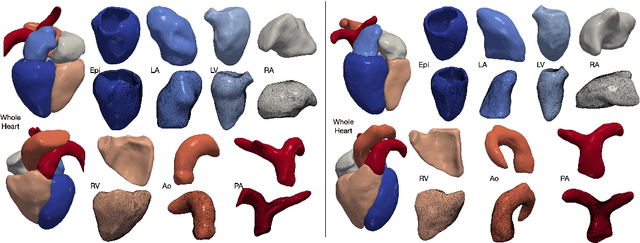
Automated construction of surface geometries of cardiac structures from volumetric medical images is important for a number of clinical applications. While deep-learning based approaches have demonstrated promising reconstruction precision, these approaches have mostly focused on voxel-wise segmentation followed by surface reconstruction and post-processing techniques. However, such approaches suffer from a number of limitations including disconnected regions or incorrect surface topology due to erroneous segmentation and stair-case artifacts due to limited segmentation resolution. We propose a novel deep-learning-based approach that directly predicts whole heart surface meshes from volumetric CT and MR image data. Our approach leverages a graph convolutional neural network to predict deformation on mesh vertices from a pre-defined mesh template to reconstruct multiple anatomical structures in a 3D image volume. Our method demonstrated promising performance of generating high-resolution and high-quality whole heart reconstructions and outperformed prior deep-learning based methods on both CT and MR data in terms of precision and surface quality. Furthermore, our method can more efficiently produce temporally-consistent and feature-corresponding surface mesh predictions for heart motion from CT or MR cine sequences, and therefore can potentially be applied for efficiently constructing 4D whole heart dynamics.

Interpolating the Trace of the Inverse of Matrix $\mathbf{A} + t \mathbf{B}$

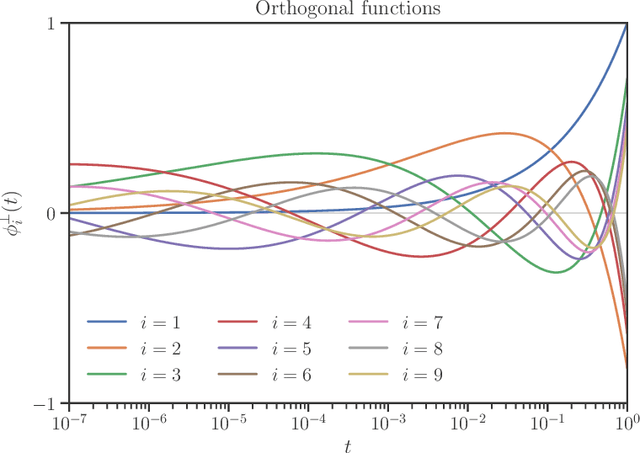
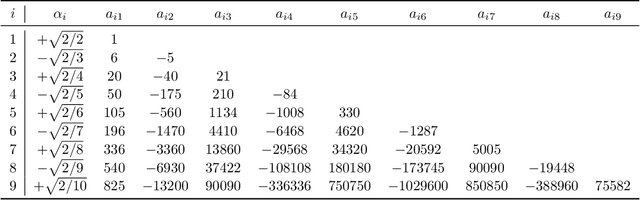
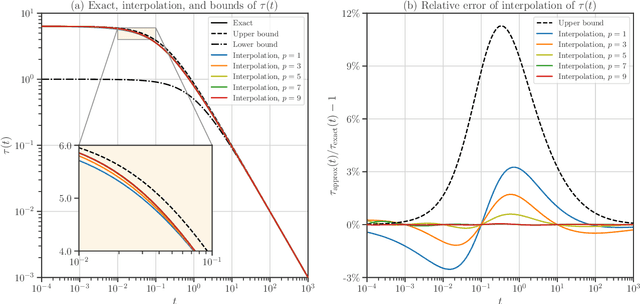
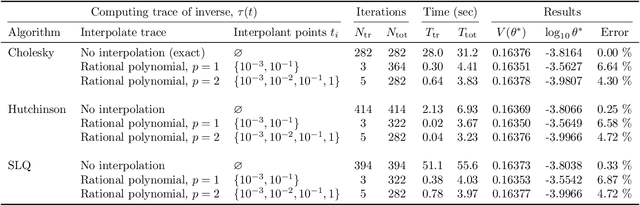
We develop heuristic interpolation methods for the function $t \mapsto \operatorname{trace}\left( (\mathbf{A} + t \mathbf{B})^{-1} \right)$, where the matrices $\mathbf{A}$ and $\mathbf{B}$ are symmetric and positive definite and $t$ is a real variable. This function is featured in many applications in statistics, machine learning, and computational physics. The presented interpolation functions are based on the modification of a sharp upper bound that we derive for this function, which is a new trace inequality for matrices. We demonstrate the accuracy and performance of the proposed method with numerical examples, namely, the marginal maximum likelihood estimation for linear Gaussian process regression and the estimation of the regularization parameter of ridge regression with the generalized cross-validation method.