Convex SGD: Generalization Without Early Stopping

We consider the generalization error associated with stochastic gradient descent on a smooth convex function over a compact set. We show the first bound on the generalization error that vanishes when the number of iterations $T$ and the dataset size $n$ go to zero at arbitrary rates; our bound scales as $\tilde{O}(1/\sqrt{T} + 1/\sqrt{n})$ with step-size $\alpha_t = 1/\sqrt{t}$. In particular, strong convexity is not needed for stochastic gradient descent to generalize well.

PEPit: computer-assisted worst-case analyses of first-order optimization methods in Python

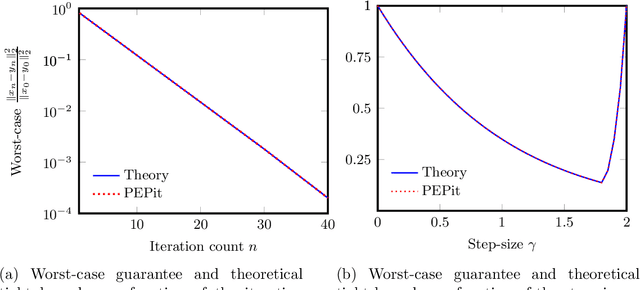
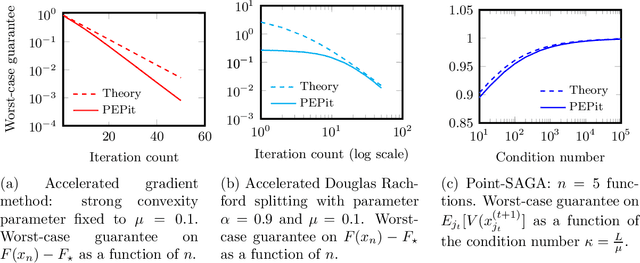
PEPit is a Python package aiming at simplifying the access to worst-case analyses of a large family of first-order optimization methods possibly involving gradient, projection, proximal, or linear optimization oracles, along with their approximate, or Bregman variants. In short, PEPit is a package enabling computer-assisted worst-case analyses of first-order optimization methods. The key underlying idea is to cast the problem of performing a worst-case analysis, often referred to as a performance estimation problem (PEP), as a semidefinite program (SDP) which can be solved numerically. For doing that, the package users are only required to write first-order methods nearly as they would have implemented them. The package then takes care of the SDP modelling parts, and the worst-case analysis is performed numerically via a standard solver.