Sample Complexity of Linear Quadratic Regulator Without Initial Stability

Inspired by REINFORCE, we introduce a novel receding-horizon algorithm for the Linear Quadratic Regulator (LQR) problem with unknown parameters. Unlike prior methods, our algorithm avoids reliance on two-point gradient estimates while maintaining the same order of sample complexity. Furthermore, it eliminates the restrictive requirement of starting with a stable initial policy, broadening its applicability. Beyond these improvements, we introduce a refined analysis of error propagation through the contraction of the Riemannian distance over the Riccati operator. This refinement leads to a better sample complexity and ensures improved convergence guarantees. Numerical simulations validate the theoretical results, demonstrating the method's practical feasibility and performance in realistic scenarios.

Analysis of Value Iteration Through Absolute Probability Sequences

Value Iteration is a widely used algorithm for solving Markov Decision Processes (MDPs). While previous studies have extensively analyzed its convergence properties, they primarily focus on convergence with respect to the infinity norm. In this work, we use absolute probability sequences to develop a new line of analysis and examine the algorithm's convergence in terms of the $L^2$ norm, offering a new perspective on its behavior and performance.

MDP Geometry, Normalization and Value Free Solvers

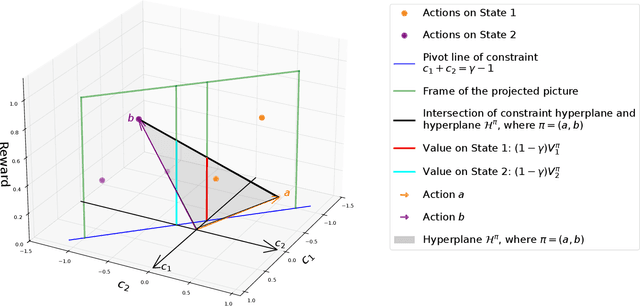
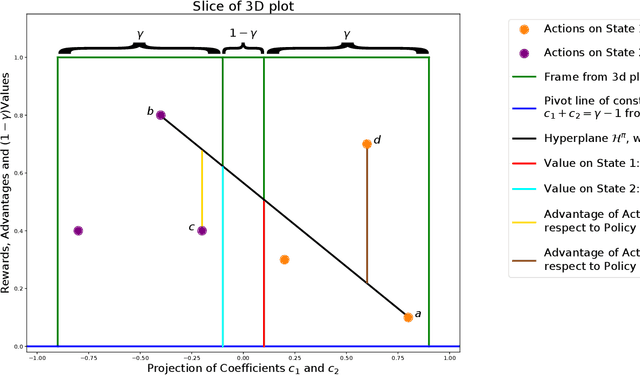
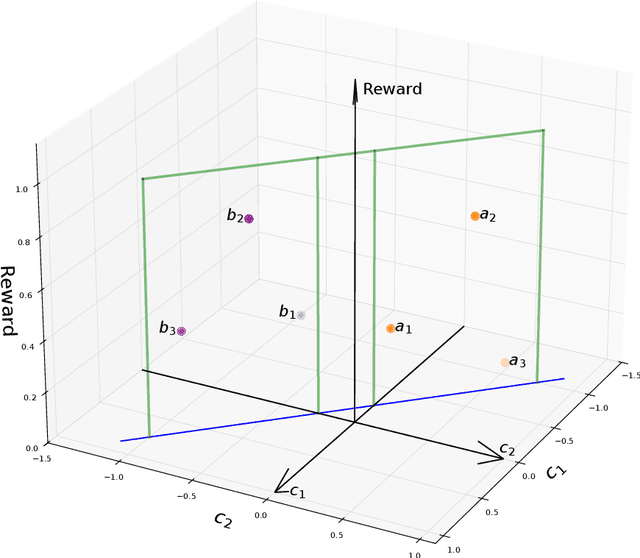
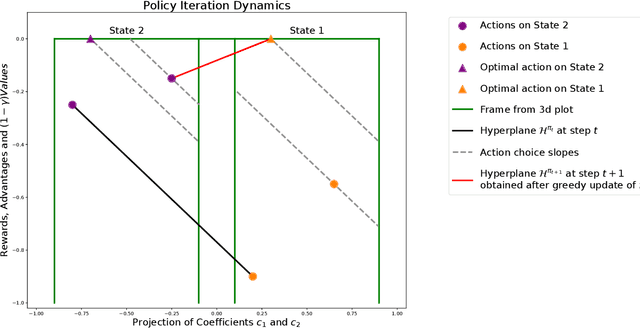
Markov Decision Process (MDP) is a common mathematical model for sequential decision-making problems. In this paper, we present a new geometric interpretation of MDP, which is useful for analyzing the dynamics of main MDP algorithms. Based on this interpretation, we demonstrate that MDPs can be split into equivalence classes with indistinguishable algorithm dynamics. The related normalization procedure allows for the design of a new class of MDP-solving algorithms that find optimal policies without computing policy values.

Tree Search for Simultaneous Move Games via Equilibrium Approximation

Neural network supported tree-search has shown strong results in a variety of perfect information multi-agent tasks. However, the performance of these methods on partial information games has generally been below competing approaches. Here we study the class of simultaneous-move games, which are a subclass of partial information games which are most similar to perfect information games: both agents know the game state with the exception of the opponent's move, which is revealed only after each agent makes its own move. Simultaneous move games include popular benchmarks such as Google Research Football and Starcraft. In this study we answer the question: can we take tree search algorithms trained through self-play from perfect information settings and adapt them to simultaneous move games without significant loss of performance? We answer this question by deriving a practical method that attempts to approximate a coarse correlated equilibrium as a subroutine within a tree search. Our algorithm works on cooperative, competitive, and mixed tasks. Our results are better than the current best MARL algorithms on a wide range of accepted baseline environments.

On Value Iteration Convergence in Connected MDPs

This paper establishes that an MDP with a unique optimal policy and ergodic associated transition matrix ensures the convergence of various versions of the Value Iteration algorithm at a geometric rate that exceeds the discount factor {\gamma} for both discounted and average-reward criteria.

Sample Complexity of the Linear Quadratic Regulator: A Reinforcement Learning Lens

We provide the first known algorithm that provably achieves $\varepsilon$-optimality within $\widetilde{\mathcal{O}}(1/\varepsilon)$ function evaluations for the discounted discrete-time LQR problem with unknown parameters, without relying on two-point gradient estimates. These estimates are known to be unrealistic in many settings, as they depend on using the exact same initialization, which is to be selected randomly, for two different policies. Our results substantially improve upon the existing literature outside the realm of two-point gradient estimates, which either leads to $\widetilde{\mathcal{O}}(1/\varepsilon^2)$ rates or heavily relies on stability assumptions.

One-Shot Averaging for Distributed TD Under Markov Sampling

We consider a distributed setup for reinforcement learning, where each agent has a copy of the same Markov Decision Process but transitions are sampled from the corresponding Markov chain independently by each agent. We show that in this setting, we can achieve a linear speedup for TD($\lambda$), a family of popular methods for policy evaluation, in the sense that $N$ agents can evaluate a policy $N$ times faster provided the target accuracy is small enough. Notably, this speedup is achieved by ``one shot averaging,'' a procedure where the agents run TD($\lambda$) with Markov sampling independently and only average their results after the final step. This significantly reduces the amount of communication required to achieve a linear speedup relative to previous work.

Convex SGD: Generalization Without Early Stopping

We consider the generalization error associated with stochastic gradient descent on a smooth convex function over a compact set. We show the first bound on the generalization error that vanishes when the number of iterations $T$ and the dataset size $n$ go to zero at arbitrary rates; our bound scales as $\tilde{O}(1/\sqrt{T} + 1/\sqrt{n})$ with step-size $\alpha_t = 1/\sqrt{t}$. In particular, strong convexity is not needed for stochastic gradient descent to generalize well.

On the Performance of Temporal Difference Learning With Neural Networks

Neural Temporal Difference (TD) Learning is an approximate temporal difference method for policy evaluation that uses a neural network for function approximation. Analysis of Neural TD Learning has proven to be challenging. In this paper we provide a convergence analysis of Neural TD Learning with a projection onto $B(\theta_0, \omega)$, a ball of fixed radius $\omega$ around the initial point $\theta_0$. We show an approximation bound of $O(\epsilon) + \tilde{O} (1/\sqrt{m})$ where $\epsilon$ is the approximation quality of the best neural network in $B(\theta_0, \omega)$ and $m$ is the width of all hidden layers in the network.

Distributed TD(0) with Almost No Communication

We provide a new non-asymptotic analysis of distributed temporal difference learning with linear function approximation. Our approach relies on ``one-shot averaging,'' where $N$ agents run identical local copies of the TD(0) method and average the outcomes only once at the very end. We demonstrate a version of the linear time speedup phenomenon, where the convergence time of the distributed process is a factor of $N$ faster than the convergence time of TD(0). This is the first result proving benefits from parallelism for temporal difference methods.