Localmax dynamics for attention in transformers and its asymptotic behavior

We introduce a new discrete-time attention model, termed the localmax dynamics, which interpolates between the classic softmax dynamics and the hardmax dynamics, where only the tokens that maximize the influence toward a given token have a positive weight. As in hardmax, uniform weights are determined by a parameter controlling neighbor influence, but the key extension lies in relaxing neighborhood interactions through an alignment-sensitivity parameter, which allows controlled deviations from pure hardmax behavior. As we prove, while the convex hull of the token states still converges to a convex polytope, its structure can no longer be fully described by a maximal alignment set, prompting the introduction of quiescent sets to capture the invariant behavior of tokens near vertices. We show that these sets play a key role in understanding the asymptotic behavior of the system, even under time-varying alignment sensitivity parameters. We further show that localmax dynamics does not exhibit finite-time convergence and provide results for vanishing, nonzero, time-varying alignment-sensitivity parameters, recovering the limiting behavior of hardmax as a by-product. Finally, we adapt Lyapunov-based methods from classical opinion dynamics, highlighting their limitations in the asymmetric setting of localmax interactions and outlining directions for future research.

Neural Lyapunov Function Approximation with Self-Supervised Reinforcement Learning

Control Lyapunov functions are traditionally used to design a controller which ensures convergence to a desired state, yet deriving these functions for nonlinear systems remains a complex challenge. This paper presents a novel, sample-efficient method for neural approximation of nonlinear Lyapunov functions, leveraging self-supervised Reinforcement Learning (RL) to enhance training data generation, particularly for inaccurately represented regions of the state space. The proposed approach employs a data-driven World Model to train Lyapunov functions from off-policy trajectories. The method is validated on both standard and goal-conditioned robotic tasks, demonstrating faster convergence and higher approximation accuracy compared to the state-of-the-art neural Lyapunov approximation baseline. The code is available at: https://github.com/CAV-Research-Lab/SACLA.git

Sample Complexity of Linear Quadratic Regulator Without Initial Stability

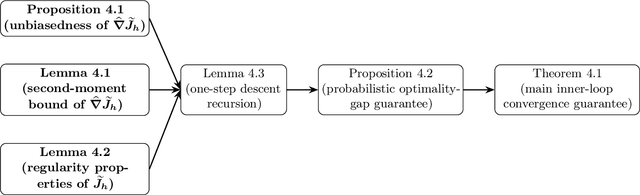
Inspired by REINFORCE, we introduce a novel receding-horizon algorithm for the Linear Quadratic Regulator (LQR) problem with unknown parameters. Unlike prior methods, our algorithm avoids reliance on two-point gradient estimates while maintaining the same order of sample complexity. Furthermore, it eliminates the restrictive requirement of starting with a stable initial policy, broadening its applicability. Beyond these improvements, we introduce a refined analysis of error propagation through the contraction of the Riemannian distance over the Riccati operator. This refinement leads to a better sample complexity and ensures improved convergence guarantees. Numerical simulations validate the theoretical results, demonstrating the method's practical feasibility and performance in realistic scenarios.

Sample Complexity of the Linear Quadratic Regulator: A Reinforcement Learning Lens

We provide the first known algorithm that provably achieves $\varepsilon$-optimality within $\widetilde{\mathcal{O}}(1/\varepsilon)$ function evaluations for the discounted discrete-time LQR problem with unknown parameters, without relying on two-point gradient estimates. These estimates are known to be unrealistic in many settings, as they depend on using the exact same initialization, which is to be selected randomly, for two different policies. Our results substantially improve upon the existing literature outside the realm of two-point gradient estimates, which either leads to $\widetilde{\mathcal{O}}(1/\varepsilon^2)$ rates or heavily relies on stability assumptions.

A Unifying Generator Loss Function for Generative Adversarial Networks

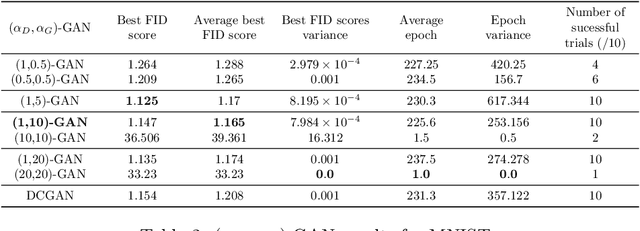
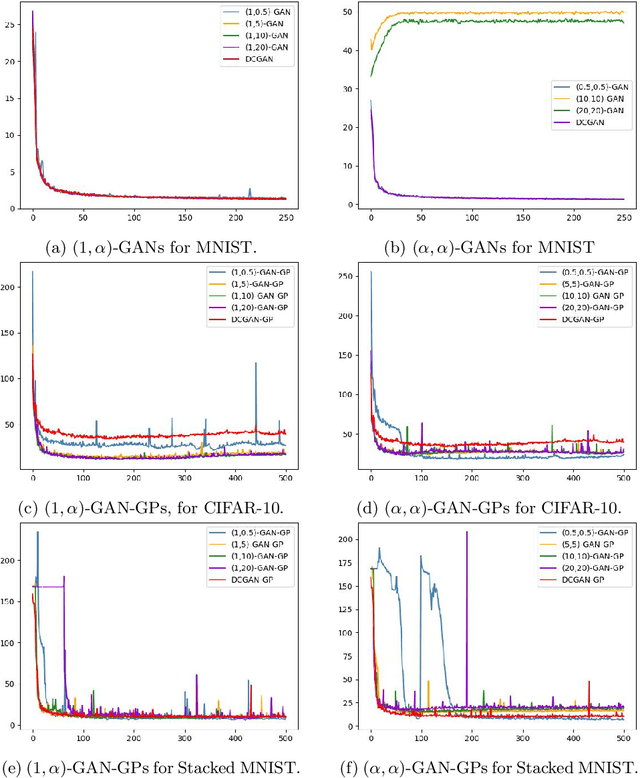
A unifying $\alpha$-parametrized generator loss function is introduced for a dual-objective generative adversarial network (GAN), which uses a canonical (or classical) discriminator loss function such as the one in the original GAN (VanillaGAN) system. The generator loss function is based on a symmetric class probability estimation type function, $\mathcal{L}_\alpha$, and the resulting GAN system is termed $\mathcal{L}_\alpha$-GAN. Under an optimal discriminator, it is shown that the generator's optimization problem consists of minimizing a Jensen-$f_\alpha$-divergence, a natural generalization of the Jensen-Shannon divergence, where $f_\alpha$ is a convex function expressed in terms of the loss function $\mathcal{L}_\alpha$. It is also demonstrated that this $\mathcal{L}_\alpha$-GAN problem recovers as special cases a number of GAN problems in the literature, including VanillaGAN, Least Squares GAN (LSGAN), Least $k$th order GAN (L$k$GAN) and the recently introduced $(\alpha_D,\alpha_G)$-GAN with $\alpha_D=1$. Finally, experimental results are conducted on three datasets, MNIST, CIFAR-10, and Stacked MNIST to illustrate the performance of various examples of the $\mathcal{L}_\alpha$-GAN system.

Achieving Utility, Fairness, and Compactness via Tunable Information Bottleneck Measures

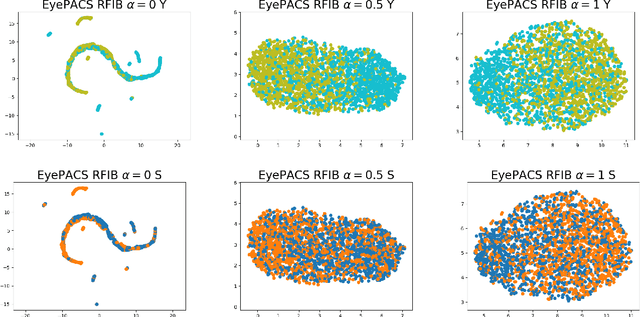
Designing machine learning algorithms that are accurate yet fair, not discriminating based on any sensitive attribute, is of paramount importance for society to accept AI for critical applications. In this article, we propose a novel fair representation learning method termed the R\'enyi Fair Information Bottleneck Method (RFIB) which incorporates constraints for utility, fairness, and compactness of representation, and apply it to image classification. A key attribute of our approach is that we consider - in contrast to most prior work - both demographic parity and equalized odds as fairness constraints, allowing for a more nuanced satisfaction of both criteria. Leveraging a variational approach, we show that our objectives yield a loss function involving classical Information Bottleneck (IB) measures and establish an upper bound in terms of the R\'enyi divergence of order $\alpha$ on the mutual information IB term measuring compactness between the input and its encoded embedding. Experimenting on three different image datasets (EyePACS, CelebA, and FairFace), we study the influence of the $\alpha$ parameter as well as two other tunable IB parameters on achieving utility/fairness trade-off goals, and show that the $\alpha$ parameter gives an additional degree of freedom that can be used to control the compactness of the representation. We evaluate the performance of our method using various utility, fairness, and compound utility/fairness metrics, showing that RFIB outperforms current state-of-the-art approaches.

Neural ODE Control for Trajectory Approximation of Continuity Equation

We consider the controllability problem for the continuity equation, corresponding to neural ordinary differential equations (ODEs), which describes how a probability measure is pushedforward by the flow. We show that the controlled continuity equation has very strong controllability properties. Particularly, a given solution of the continuity equation corresponding to a bounded Lipschitz vector field defines a trajectory on the set of probability measures. For this trajectory, we show that there exist piecewise constant training weights for a neural ODE such that the solution of the continuity equation corresponding to the neural ODE is arbitrarily close to it. As a corollary to this result, we establish that the continuity equation of the neural ODE is approximately controllable on the set of compactly supported probability measures that are absolutely continuous with respect to the Lebesgue measure.

Renyi Fair Information Bottleneck for Image Classification

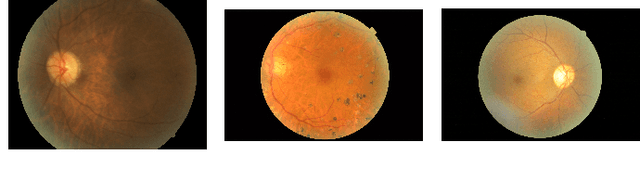
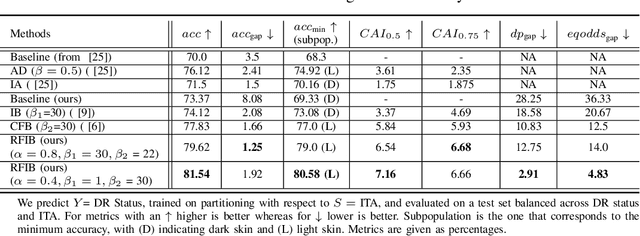
We develop a novel method for ensuring fairness in machine learning which we term as the Renyi Fair Information Bottleneck (RFIB). We consider two different fairness constraints - demographic parity and equalized odds - for learning fair representations and derive a loss function via a variational approach that uses Renyi's divergence with its tunable parameter $\alpha$ and that takes into account the triple constraints of utility, fairness, and compactness of representation. We then evaluate the performance of our method for image classification using the EyePACS medical imaging dataset, showing it outperforms competing state of the art techniques with performance measured using a variety of compound utility/fairness metrics, including accuracy gap and Rawls' minimal accuracy.

A Small Gain Analysis of Single Timescale Actor Critic

We consider a version of actor-critic which uses proportional step-sizes and only one critic update with a single sample from the stationary distribution per actor step. We provide an analysis of this method using the small-gain theorem. Specifically, we prove that this method can be used to find a stationary point, and that the resulting sample complexity improves the state of the art for actor-critic methods to $O \left(\mu^{-2} \epsilon^{-2} \right)$ to find an $\epsilon$-approximate stationary point where $\mu$ is the condition number associated with the critic.

Universal Approximation Power of Deep Neural Networks via Nonlinear Control Theory

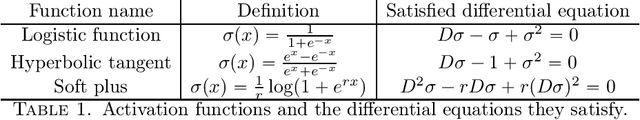
In this paper, we explain the universal approximation capabilities of deep neural networks through geometric nonlinear control. Inspired by recent work establishing links between residual networks and control systems, we provide a general sufficient condition for a residual network to have the power of universal approximation by asking the activation function, or one of its derivatives, to satisfy a quadratic differential equation. Many activation functions used in practice satisfy this assumption, exactly or approximately, and we show this property to be sufficient for an adequately deep neural network with n states to approximate arbitrarily well any continuous function defined on a compact subset of R^n. We further show this result to hold for very simple architectures, where the weights only need to assume two values. The key technical contribution consists of relating the universal approximation problem to controllability of an ensemble of control systems corresponding to a residual network, and to leverage classical Lie algebraic techniques to characterize controllability.