Secure Safety Filter: Towards Safe Flight Control under Sensor Attacks

Modern autopilot systems are prone to sensor attacks that can jeopardize flight safety. To mitigate this risk, we proposed a modular solution: the secure safety filter, which extends the well-established control barrier function (CBF)-based safety filter to account for, and mitigate, sensor attacks. This module consists of a secure state reconstructor (which generates plausible states) and a safety filter (which computes the safe control input that is closest to the nominal one). Differing from existing work focusing on linear, noise-free systems, the proposed secure safety filter handles bounded measurement noise and, by leveraging reduced-order model techniques, is applicable to the nonlinear dynamics of drones. Software-in-the-loop simulations and drone hardware experiments demonstrate the effectiveness of the secure safety filter in rendering the system safe in the presence of sensor attacks.

The Asymptotic Behavior of Attention in Transformers

A key component of transformers is the attention mechanism orchestrating how each token influences the propagation of every other token through a transformer. In this paper we provide a rigorous, mathematical analysis of the asymptotic properties of attention in transformers. Although we present several results based on different assumptions, all of them point to the same conclusion, all tokens asymptotically converge to each other, a phenomenon that has been empirically reported in the literature. Our findings are carefully compared with existing theoretical results and illustrated by simulations and experimental studies using the GPT-2 model.

Meanings and Feelings of Large Language Models: Observability of Latent States in Generative AI

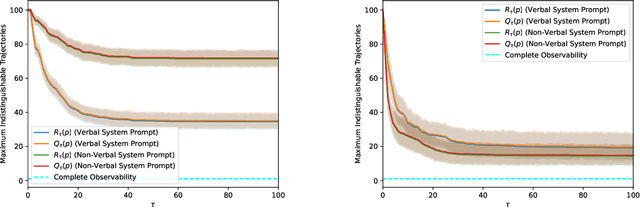
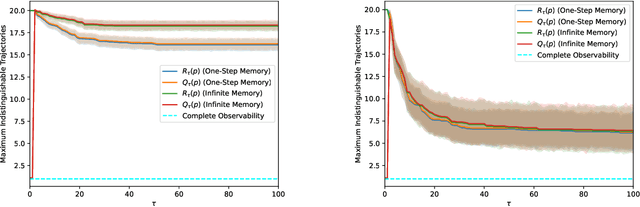
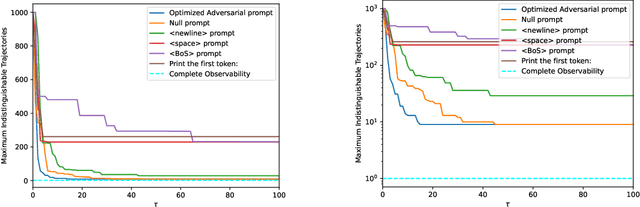
We tackle the question of whether Large Language Models (LLMs), viewed as dynamical systems with state evolving in the embedding space of symbolic tokens, are observable. That is, whether there exist multiple 'mental' state trajectories that yield the same sequence of generated tokens, or sequences that belong to the same Nerode equivalence class ('meaning'). If not observable, mental state trajectories ('experiences') evoked by an input ('perception') or by feedback from the model's own state ('thoughts') could remain self-contained and evolve unbeknown to the user while being potentially accessible to the model provider. Such "self-contained experiences evoked by perception or thought" are akin to what the American Psychological Association (APA) defines as 'feelings'. Beyond the lexical curiosity, we show that current LLMs implemented by autoregressive Transformers cannot have 'feelings' according to this definition: The set of state trajectories indistinguishable from the tokenized output is a singleton. But if there are 'system prompts' not visible to the user, then the set of indistinguishable trajectories becomes non-trivial, and there can be multiple state trajectories that yield the same verbalized output. We prove these claims analytically, and show examples of modifications to standard LLMs that engender such 'feelings.' Our analysis sheds light on possible designs that would enable a model to perform non-trivial computation that is not visible to the user, as well as on controls that the provider of services using the model could take to prevent unintended behavior.

Heat Death of Generative Models in Closed-Loop Learning

Improvement and adoption of generative machine learning models is rapidly accelerating, as exemplified by the popularity of LLMs (Large Language Models) for text, and diffusion models for image generation.As generative models become widespread, data they generate is incorporated into shared content through the public web. This opens the question of what happens when data generated by a model is fed back to the model in subsequent training campaigns. This is a question about the stability of the training process, whether the distribution of publicly accessible content, which we refer to as "knowledge", remains stable or collapses. Small scale empirical experiments reported in the literature show that this closed-loop training process is prone to degenerating. Models may start producing gibberish data, or sample from only a small subset of the desired data distribution (a phenomenon referred to as mode collapse). So far there has been only limited theoretical understanding of this process, in part due to the complexity of the deep networks underlying these generative models. The aim of this paper is to provide insights into this process (that we refer to as "generative closed-loop learning") by studying the learning dynamics of generative models that are fed back their own produced content in addition to their original training dataset. The sampling of many of these models can be controlled via a "temperature" parameter. Using dynamical systems tools, we show that, unless a sufficient amount of external data is introduced at each iteration, any non-trivial temperature leads the model to asymptotically degenerate. In fact, either the generative distribution collapses to a small set of outputs, or becomes uniform over a large set of outputs.

Taming AI Bots: Controllability of Neural States in Large Language Models

We tackle the question of whether an agent can, by suitable choice of prompts, control an AI bot to any state. To that end, we first introduce a formal definition of ``meaning'' that is amenable to analysis. Then, we characterize ``meaningful data'' on which large language models (LLMs) are ostensibly trained, and ``well-trained LLMs'' through conditions that are largely met by today's LLMs. While a well-trained LLM constructs an embedding space of meanings that is Euclidean, meanings themselves do not form a vector (linear) subspace, but rather a quotient space within. We then characterize the subset of meanings that can be reached by the state of the LLMs for some input prompt, and show that a well-trained bot can reach any meaning albeit with small probability. We then introduce a stronger notion of controllability as {\em almost certain reachability}, and show that, when restricted to the space of meanings, an AI bot is controllable. We do so after introducing a functional characterization of attentive AI bots, and finally derive necessary and sufficient conditions for controllability. The fact that AI bots are controllable means that an adversary could steer them towards any state. However, the sampling process can be designed to counteract adverse actions and avoid reaching undesirable regions of state space before their boundary is crossed.

Learning to control from expert demonstrations

In this paper, we revisit the problem of learning a stabilizing controller from a finite number of demonstrations by an expert. By first focusing on feedback linearizable systems, we show how to combine expert demonstrations into a stabilizing controller, provided that demonstrations are sufficiently long and there are at least $n+1$ of them, where $n$ is the number of states of the system being controlled. When we have more than $n+1$ demonstrations, we discuss how to optimally choose the best $n+1$ demonstrations to construct the stabilizing controller. We then extend these results to a class of systems that can be embedded into a higher-dimensional system containing a chain of integrators. The feasibility of the proposed algorithm is demonstrated by applying it on a CrazyFlie 2.0 quadrotor.

Dirty derivatives for output feedback stabilization

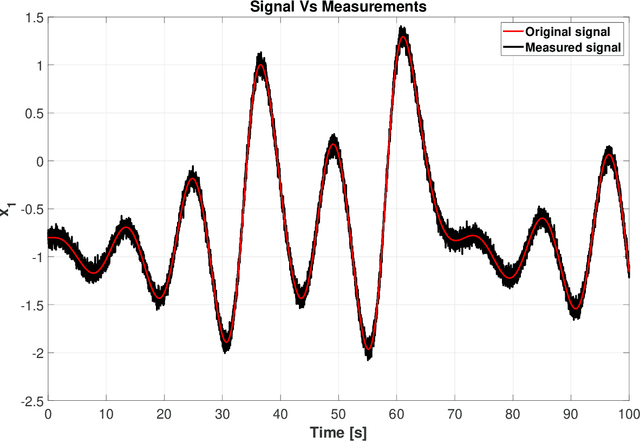
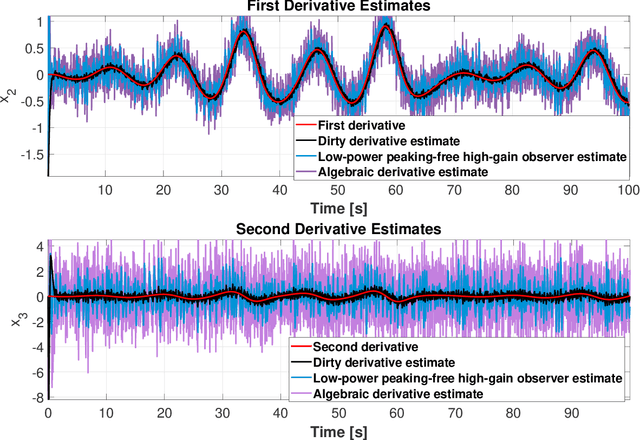
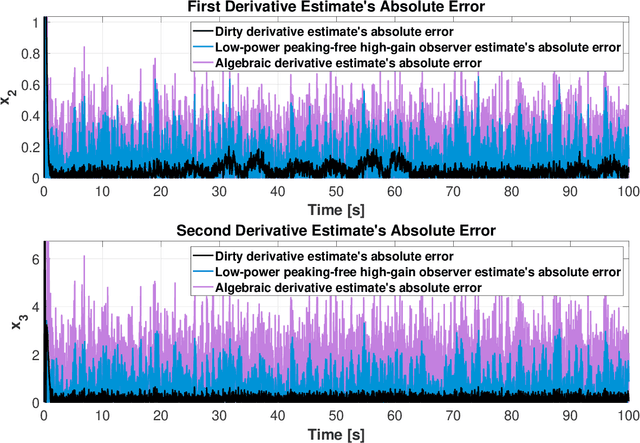
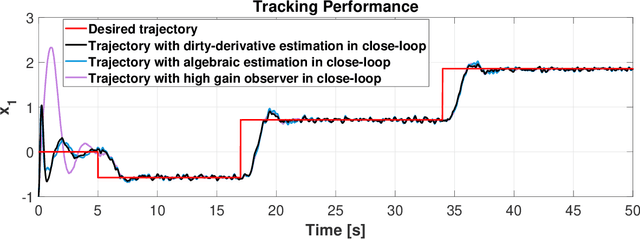
Dirty derivatives are routinely used in industrial settings, particularly in the implementation of the derivative term in PID control, and are especially appealing due to their noise-attenuation and model-free characteristics. In this paper, we provide a Lyapunov-based proof for the stability of linear time-invariant control systems in controller canonical form when utilizing dirty derivatives in place of observers for the purpose of output feedback. This is, to the best of the authors' knowledge, the first time that stability proofs are provided for the use of dirty derivatives in lieu of derivatives of different orders. In the spirit of adaptive control, we also show how dirty derivatives can be used for output feedback control when the control gain is unknown.

Learned Uncertainty Calibration for Visual Inertial Localization

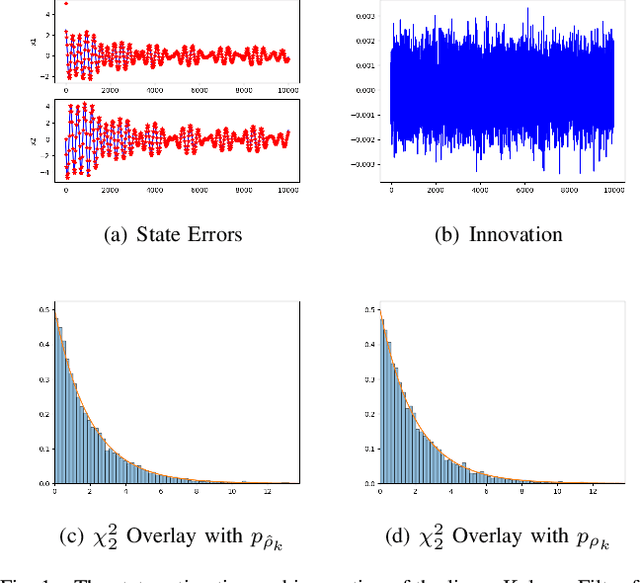
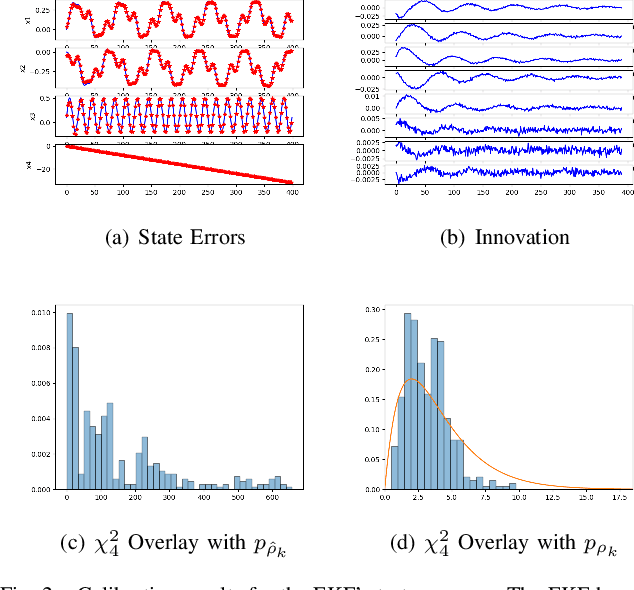
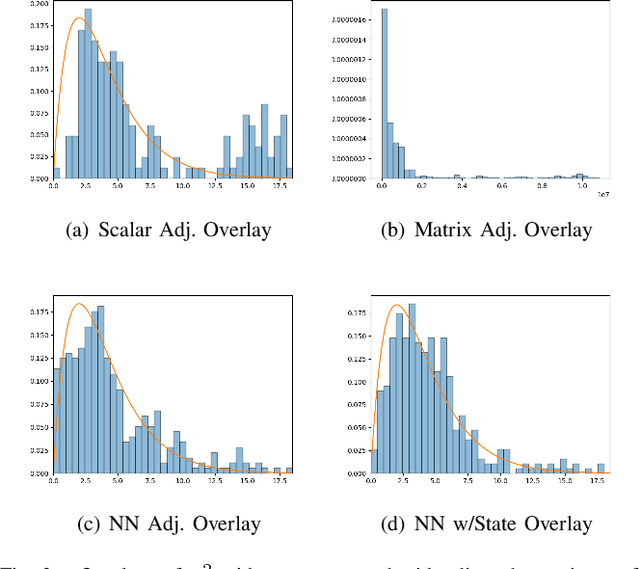
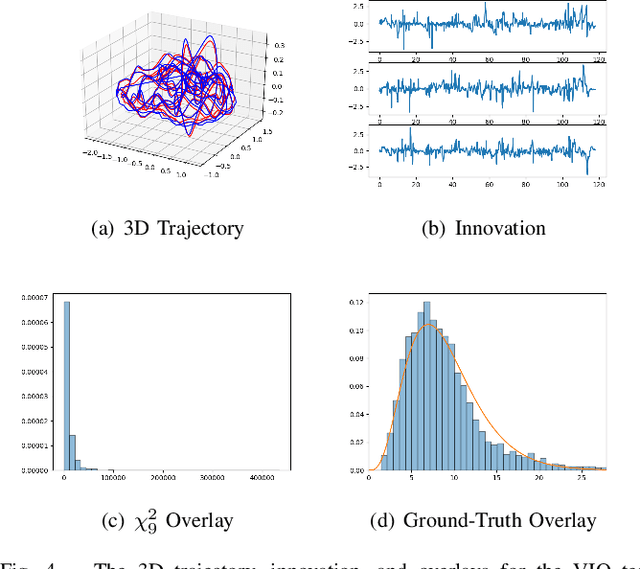
The widely-used Extended Kalman Filter (EKF) provides a straightforward recipe to estimate the mean and covariance of the state given all past measurements in a causal and recursive fashion. For a wide variety of applications, the EKF is known to produce accurate estimates of the mean and typically inaccurate estimates of the covariance. For applications in visual inertial localization, we show that inaccuracies in the covariance estimates are \emph{systematic}, i.e. it is possible to learn a nonlinear map from the empirical ground truth to the estimated one. This is demonstrated on both a standard EKF in simulation and a Visual Inertial Odometry system on real-world data.

Joint Continuous and Discrete Model Selection via Submodularity

In model selection problems for machine learning, the desire for a well-performing model with meaningful structure is typically expressed through a regularized optimization problem. In many scenarios, however, the meaningful structure is specified in some discrete space, leading to difficult nonconvex optimization problems. In this paper, we relate the model selection problem with structure-promoting regularizers to submodular function minimization defined with continuous and discrete arguments. In particular, we leverage submodularity theory to identify a class of these problems that can be solved exactly and efficiently with an agnostic combination of discrete and continuous optimization routines. We show how simple continuous or discrete constraints can also be handled for certain problem classes, motivated by robust optimization. Finally, we numerically validate our theoretical results with several proof-of-concept examples, comparing against state-of-the-art algorithms.

Universal Approximation Power of Deep Neural Networks via Nonlinear Control Theory

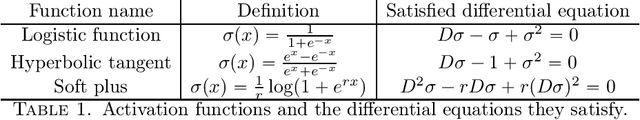
In this paper, we explain the universal approximation capabilities of deep neural networks through geometric nonlinear control. Inspired by recent work establishing links between residual networks and control systems, we provide a general sufficient condition for a residual network to have the power of universal approximation by asking the activation function, or one of its derivatives, to satisfy a quadratic differential equation. Many activation functions used in practice satisfy this assumption, exactly or approximately, and we show this property to be sufficient for an adequately deep neural network with n states to approximate arbitrarily well any continuous function defined on a compact subset of R^n. We further show this result to hold for very simple architectures, where the weights only need to assume two values. The key technical contribution consists of relating the universal approximation problem to controllability of an ensemble of control systems corresponding to a residual network, and to leverage classical Lie algebraic techniques to characterize controllability.