Universal Approximation Power of Deep Neural Networks via Nonlinear Control Theory

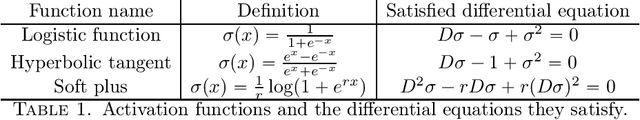
In this paper, we explain the universal approximation capabilities of deep neural networks through geometric nonlinear control. Inspired by recent work establishing links between residual networks and control systems, we provide a general sufficient condition for a residual network to have the power of universal approximation by asking the activation function, or one of its derivatives, to satisfy a quadratic differential equation. Many activation functions used in practice satisfy this assumption, exactly or approximately, and we show this property to be sufficient for an adequately deep neural network with n states to approximate arbitrarily well any continuous function defined on a compact subset of R^n. We further show this result to hold for very simple architectures, where the weights only need to assume two values. The key technical contribution consists of relating the universal approximation problem to controllability of an ensemble of control systems corresponding to a residual network, and to leverage classical Lie algebraic techniques to characterize controllability.