Learning to control from expert demonstrations

In this paper, we revisit the problem of learning a stabilizing controller from a finite number of demonstrations by an expert. By first focusing on feedback linearizable systems, we show how to combine expert demonstrations into a stabilizing controller, provided that demonstrations are sufficiently long and there are at least $n+1$ of them, where $n$ is the number of states of the system being controlled. When we have more than $n+1$ demonstrations, we discuss how to optimally choose the best $n+1$ demonstrations to construct the stabilizing controller. We then extend these results to a class of systems that can be embedded into a higher-dimensional system containing a chain of integrators. The feasibility of the proposed algorithm is demonstrated by applying it on a CrazyFlie 2.0 quadrotor.

Dirty derivatives for output feedback stabilization

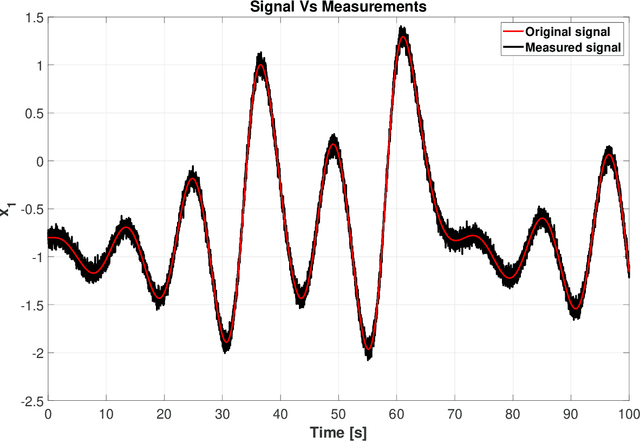
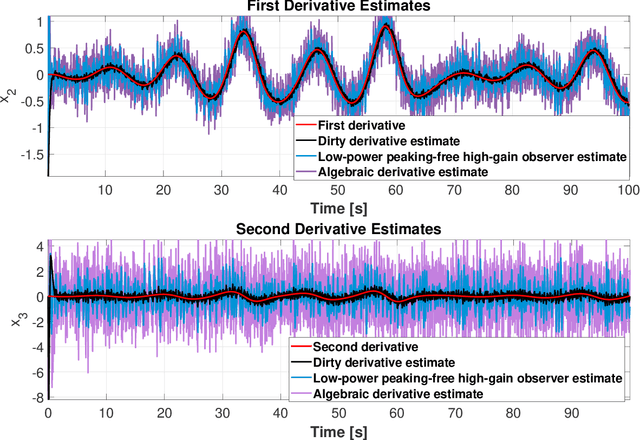
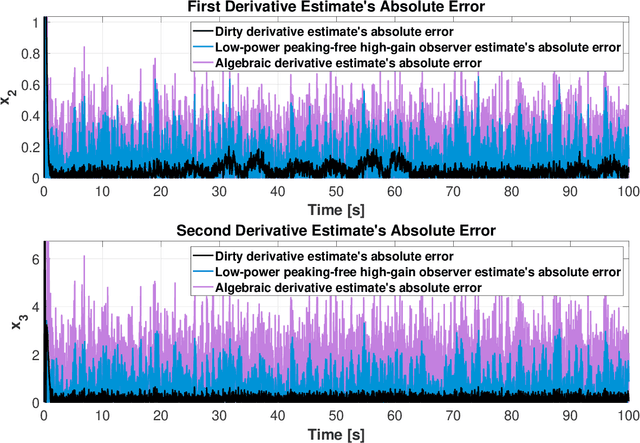
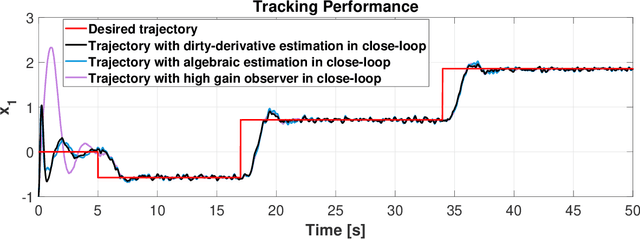
Dirty derivatives are routinely used in industrial settings, particularly in the implementation of the derivative term in PID control, and are especially appealing due to their noise-attenuation and model-free characteristics. In this paper, we provide a Lyapunov-based proof for the stability of linear time-invariant control systems in controller canonical form when utilizing dirty derivatives in place of observers for the purpose of output feedback. This is, to the best of the authors' knowledge, the first time that stability proofs are provided for the use of dirty derivatives in lieu of derivatives of different orders. In the spirit of adaptive control, we also show how dirty derivatives can be used for output feedback control when the control gain is unknown.