Meanings and Feelings of Large Language Models: Observability of Latent States in Generative AI

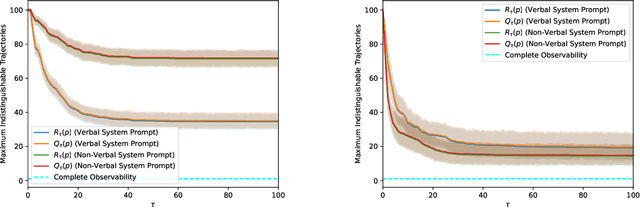
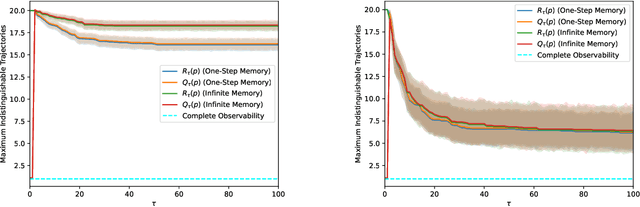
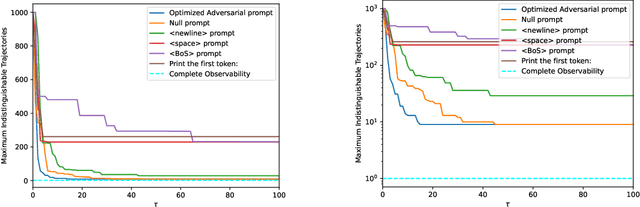
We tackle the question of whether Large Language Models (LLMs), viewed as dynamical systems with state evolving in the embedding space of symbolic tokens, are observable. That is, whether there exist multiple 'mental' state trajectories that yield the same sequence of generated tokens, or sequences that belong to the same Nerode equivalence class ('meaning'). If not observable, mental state trajectories ('experiences') evoked by an input ('perception') or by feedback from the model's own state ('thoughts') could remain self-contained and evolve unbeknown to the user while being potentially accessible to the model provider. Such "self-contained experiences evoked by perception or thought" are akin to what the American Psychological Association (APA) defines as 'feelings'. Beyond the lexical curiosity, we show that current LLMs implemented by autoregressive Transformers cannot have 'feelings' according to this definition: The set of state trajectories indistinguishable from the tokenized output is a singleton. But if there are 'system prompts' not visible to the user, then the set of indistinguishable trajectories becomes non-trivial, and there can be multiple state trajectories that yield the same verbalized output. We prove these claims analytically, and show examples of modifications to standard LLMs that engender such 'feelings.' Our analysis sheds light on possible designs that would enable a model to perform non-trivial computation that is not visible to the user, as well as on controls that the provider of services using the model could take to prevent unintended behavior.

Heat Death of Generative Models in Closed-Loop Learning

Improvement and adoption of generative machine learning models is rapidly accelerating, as exemplified by the popularity of LLMs (Large Language Models) for text, and diffusion models for image generation.As generative models become widespread, data they generate is incorporated into shared content through the public web. This opens the question of what happens when data generated by a model is fed back to the model in subsequent training campaigns. This is a question about the stability of the training process, whether the distribution of publicly accessible content, which we refer to as "knowledge", remains stable or collapses. Small scale empirical experiments reported in the literature show that this closed-loop training process is prone to degenerating. Models may start producing gibberish data, or sample from only a small subset of the desired data distribution (a phenomenon referred to as mode collapse). So far there has been only limited theoretical understanding of this process, in part due to the complexity of the deep networks underlying these generative models. The aim of this paper is to provide insights into this process (that we refer to as "generative closed-loop learning") by studying the learning dynamics of generative models that are fed back their own produced content in addition to their original training dataset. The sampling of many of these models can be controlled via a "temperature" parameter. Using dynamical systems tools, we show that, unless a sufficient amount of external data is introduced at each iteration, any non-trivial temperature leads the model to asymptotically degenerate. In fact, either the generative distribution collapses to a small set of outputs, or becomes uniform over a large set of outputs.

Dirty derivatives for output feedback stabilization

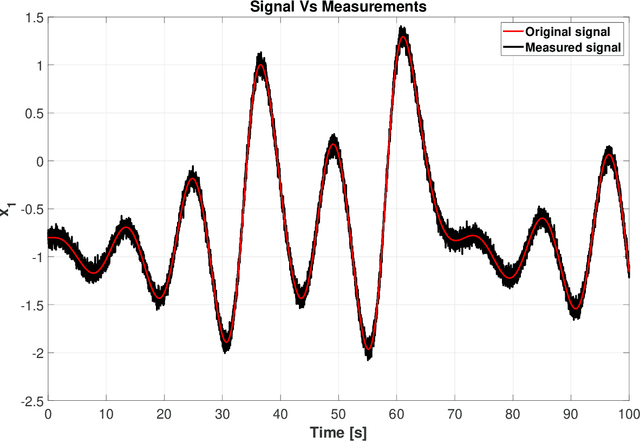
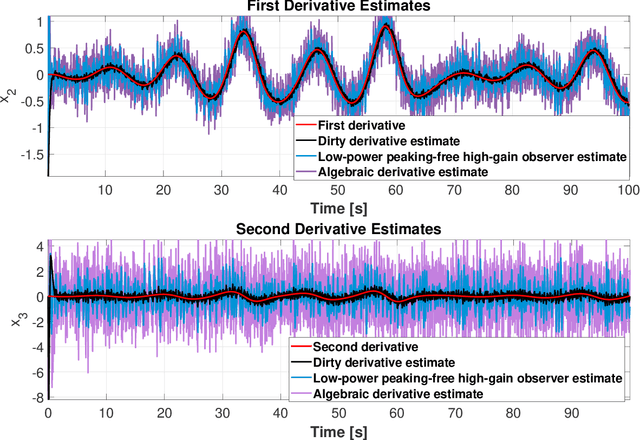
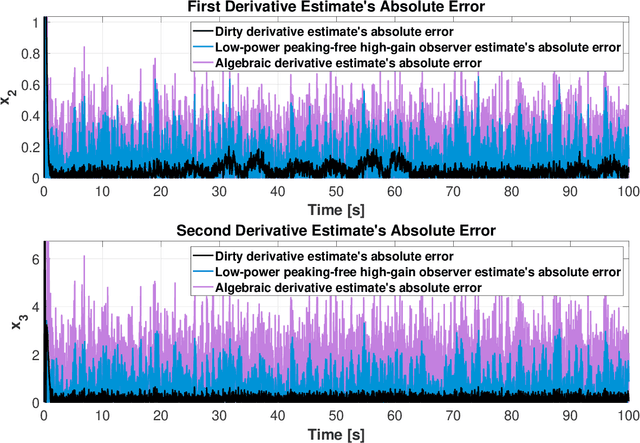
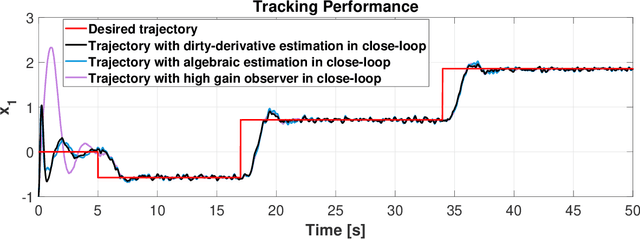
Dirty derivatives are routinely used in industrial settings, particularly in the implementation of the derivative term in PID control, and are especially appealing due to their noise-attenuation and model-free characteristics. In this paper, we provide a Lyapunov-based proof for the stability of linear time-invariant control systems in controller canonical form when utilizing dirty derivatives in place of observers for the purpose of output feedback. This is, to the best of the authors' knowledge, the first time that stability proofs are provided for the use of dirty derivatives in lieu of derivatives of different orders. In the spirit of adaptive control, we also show how dirty derivatives can be used for output feedback control when the control gain is unknown.