Dirty derivatives for output feedback stabilization
Paper and Code
Feb 04, 2022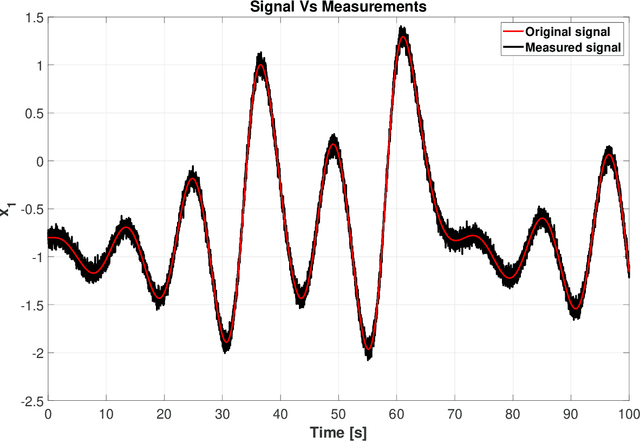
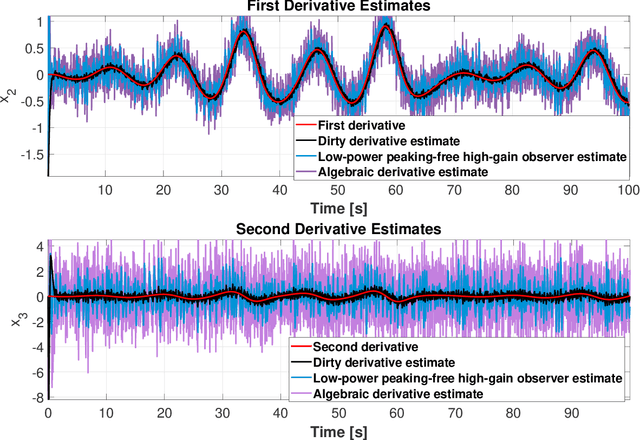
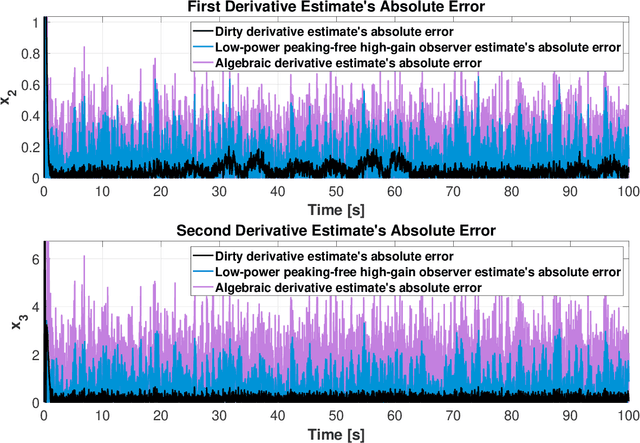
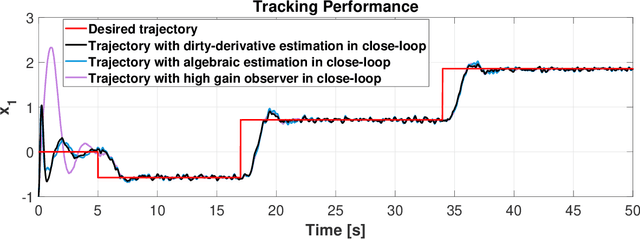
Dirty derivatives are routinely used in industrial settings, particularly in the implementation of the derivative term in PID control, and are especially appealing due to their noise-attenuation and model-free characteristics. In this paper, we provide a Lyapunov-based proof for the stability of linear time-invariant control systems in controller canonical form when utilizing dirty derivatives in place of observers for the purpose of output feedback. This is, to the best of the authors' knowledge, the first time that stability proofs are provided for the use of dirty derivatives in lieu of derivatives of different orders. In the spirit of adaptive control, we also show how dirty derivatives can be used for output feedback control when the control gain is unknown.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge