Learned Uncertainty Calibration for Visual Inertial Localization
Paper and Code
Oct 05, 2021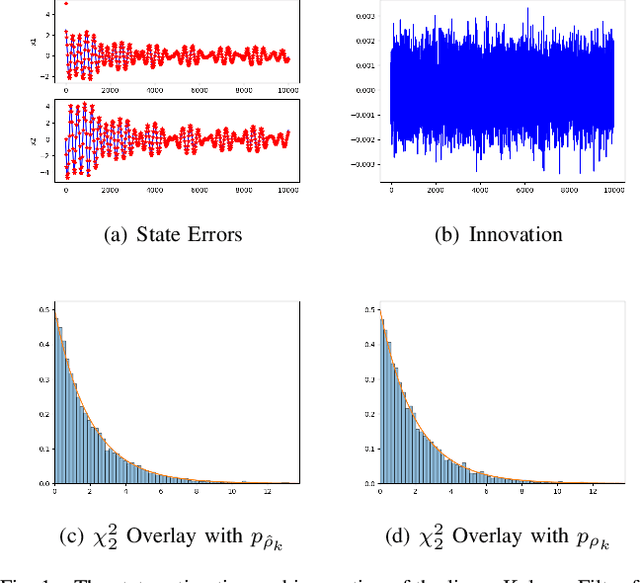
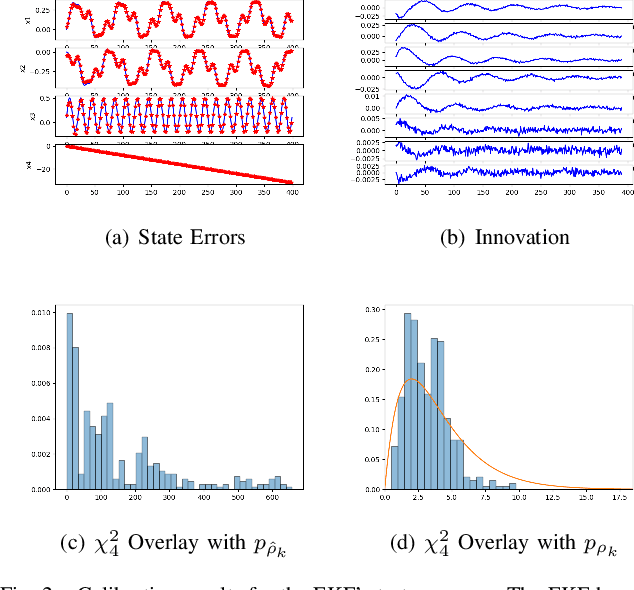
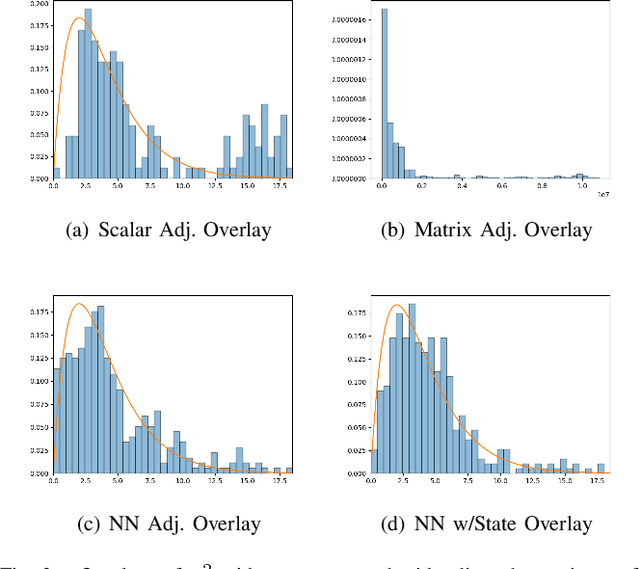
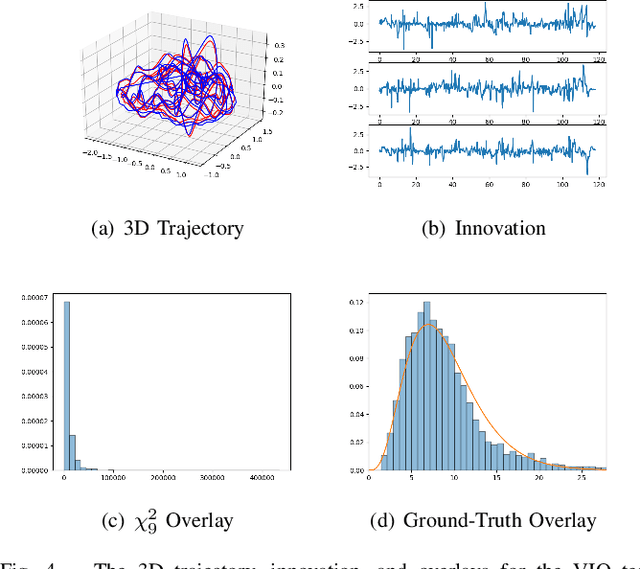
The widely-used Extended Kalman Filter (EKF) provides a straightforward recipe to estimate the mean and covariance of the state given all past measurements in a causal and recursive fashion. For a wide variety of applications, the EKF is known to produce accurate estimates of the mean and typically inaccurate estimates of the covariance. For applications in visual inertial localization, we show that inaccuracies in the covariance estimates are \emph{systematic}, i.e. it is possible to learn a nonlinear map from the empirical ground truth to the estimated one. This is demonstrated on both a standard EKF in simulation and a Visual Inertial Odometry system on real-world data.
* Published in International Conference on Robotics and Automation
(ICRA) 2021
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge