Score Matching Diffusion Based Feedback Control and Planning of Nonlinear Systems

We propose a novel control-theoretic framework that leverages principles from generative modeling -- specifically, Denoising Diffusion Probabilistic Models (DDPMs) -- to stabilize control-affine systems with nonholonomic constraints. Unlike traditional stochastic approaches, which rely on noise-driven dynamics in both forward and reverse processes, our method crucially eliminates the need for noise in the reverse phase, making it particularly relevant for control applications. We introduce two formulations: one where noise perturbs all state dimensions during the forward phase while the control system enforces time reversal deterministically, and another where noise is restricted to the control channels, embedding system constraints directly into the forward process. For controllable nonlinear drift-free systems, we prove that deterministic feedback laws can exactly reverse the forward process, ensuring that the system's probability density evolves correctly without requiring artificial diffusion in the reverse phase. Furthermore, for linear time-invariant systems, we establish a time-reversal result under the second formulation. By eliminating noise in the backward process, our approach provides a more practical alternative to machine learning-based denoising methods, which are unsuitable for control applications due to the presence of stochasticity. We validate our results through numerical simulations on benchmark systems, including a unicycle model in a domain with obstacles, a driftless five-dimensional system, and a four-dimensional linear system, demonstrating the potential for applying diffusion-inspired techniques in linear, nonlinear, and settings with state space constraints.

The Ground Cost for Optimal Transport of Angular Velocity

We revisit the optimal transport problem over angular velocity dynamics given by the controlled Euler equation. The solution of this problem enables stochastic guidance of spin states of a rigid body (e.g., spacecraft) over hard deadline constraint by transferring a given initial state statistics to a desired terminal state statistics. This is an instance of generalized optimal transport over a nonlinear dynamical system. While prior work has reported existence-uniqueness and numerical solution of this dynamical optimal transport problem, here we present structural results about the equivalent Kantorovich a.k.a. optimal coupling formulation. Specifically, we focus on deriving the ground cost for the associated Kantorovich optimal coupling formulation. The ground cost equals to the cost of transporting unit amount of mass from a specific realization of the initial or source joint probability measure to a realization of the terminal or target joint probability measure, and determines the Kantorovich formulation. Finding the ground cost leads to solving a structured deterministic nonlinear optimal control problem, which is shown to be amenable to an analysis technique pioneered by Athans et. al. We show that such techniques have broader applicability in determining the ground cost (thus Kantorovich formulation) for a class of generalized optimal mass transport problems involving nonlinear dynamics with translated norm-invariant drift.

Quantitative Flow Approximation Properties of Narrow Neural ODEs

In this note, we revisit the problem of flow approximation properties of neural ordinary differential equations (NODEs). The approximation properties have been considered as a flow controllability problem in recent literature. The neural ODE is considered {\it narrow} when the parameters have dimension equal to the input of the neural network, and hence have limited width. We derive the relation of narrow NODEs in approximating flows of shallow but wide NODEs. Due to existing results on approximation properties of shallow neural networks, this facilitates understanding which kind of flows of dynamical systems can be approximated using narrow neural ODEs. While approximation properties of narrow NODEs have been established in literature, the proofs often involve extensive constructions or require invoking deep controllability theorems from control theory. In this paper, we provide a simpler proof technique that involves only ideas from ODEs and Gr{\"o}nwall's lemma. Moreover, we provide an estimate on the number of switches needed for the time dependent weights of the narrow NODE to mimic the behavior of a NODE with a single layer wide neural network as the velocity field.

Denoising Diffusion-Based Control of Nonlinear Systems

We propose a novel approach based on Denoising Diffusion Probabilistic Models (DDPMs) to control nonlinear dynamical systems. DDPMs are the state-of-art of generative models that have achieved success in a wide variety of sampling tasks. In our framework, we pose the feedback control problem as a generative task of drawing samples from a target set under control system constraints. The forward process of DDPMs constructs trajectories originating from a target set by adding noise. We learn to control a dynamical system in reverse such that the terminal state belongs to the target set. For control-affine systems without drift, we prove that the control system can exactly track the trajectory of the forward process in reverse, whenever the the Lie bracket based condition for controllability holds. We numerically study our approach on various nonlinear systems and verify our theoretical results. We also conduct numerical experiments for cases beyond our theoretical results on a physics-engine.

Noise in the reverse process improves the approximation capabilities of diffusion models

In Score based Generative Modeling (SGMs), the state-of-the-art in generative modeling, stochastic reverse processes are known to perform better than their deterministic counterparts. This paper delves into the heart of this phenomenon, comparing neural ordinary differential equations (ODEs) and neural stochastic differential equations (SDEs) as reverse processes. We use a control theoretic perspective by posing the approximation of the reverse process as a trajectory tracking problem. We analyze the ability of neural SDEs to approximate trajectories of the Fokker-Planck equation, revealing the advantages of stochasticity. First, neural SDEs exhibit a powerful regularizing effect, enabling $L^2$ norm trajectory approximation surpassing the Wasserstein metric approximation achieved by neural ODEs under similar conditions, even when the reference vector field or score function is not Lipschitz. Applying this result, we establish the class of distributions that can be sampled using score matching in SGMs, relaxing the Lipschitz requirement on the gradient of the data distribution in existing literature. Second, we show that this approximation property is preserved when network width is limited to the input dimension of the network. In this limited width case, the weights act as control inputs, framing our analysis as a controllability problem for neural SDEs in probability density space. This sheds light on how noise helps to steer the system towards the desired solution and illuminates the empirical success of stochasticity in generative modeling.

Learning on Manifolds: Universal Approximations Properties using Geometric Controllability Conditions for Neural ODEs

In numerous robotics and mechanical engineering applications, among others, data is often constrained on smooth manifolds due to the presence of rotational degrees of freedom. Common datadriven and learning-based methods such as neural ordinary differential equations (ODEs), however, typically fail to satisfy these manifold constraints and perform poorly for these applications. To address this shortcoming, in this paper we study a class of neural ordinary differential equations that, by design, leave a given manifold invariant, and characterize their properties by leveraging the controllability properties of control affine systems. In particular, using a result due to Agrachev and Caponigro on approximating diffeomorphisms with flows of feedback control systems, we show that any map that can be represented as the flow of a manifold-constrained dynamical system can also be approximated using the flow of manifold-constrained neural ODE, whenever a certain controllability condition is satisfied. Additionally, we show that this universal approximation property holds when the neural ODE has limited width in each layer, thus leveraging the depth of network instead for approximation. We verify our theoretical findings using numerical experiments on PyTorch for the manifolds S2 and the 3-dimensional orthogonal group SO(3), which are model manifolds for mechanical systems such as spacecrafts and satellites. We also compare the performance of the manifold invariant neural ODE with classical neural ODEs that ignore the manifold invariant properties and show the superiority of our approach in terms of accuracy and sample complexity.

Neural ODE Control for Trajectory Approximation of Continuity Equation

We consider the controllability problem for the continuity equation, corresponding to neural ordinary differential equations (ODEs), which describes how a probability measure is pushedforward by the flow. We show that the controlled continuity equation has very strong controllability properties. Particularly, a given solution of the continuity equation corresponding to a bounded Lipschitz vector field defines a trajectory on the set of probability measures. For this trajectory, we show that there exist piecewise constant training weights for a neural ODE such that the solution of the continuity equation corresponding to the neural ODE is arbitrarily close to it. As a corollary to this result, we establish that the continuity equation of the neural ODE is approximately controllable on the set of compactly supported probability measures that are absolutely continuous with respect to the Lebesgue measure.

A blob method for inhomogeneous diffusion with applications to multi-agent control and sampling

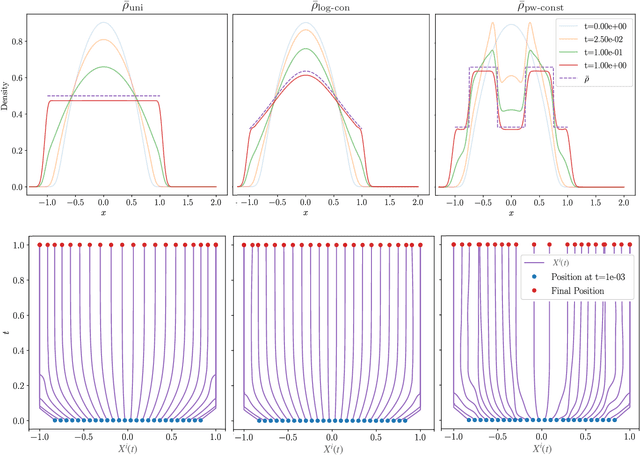
As a counterpoint to classical stochastic particle methods for linear diffusion equations, we develop a deterministic particle method for the weighted porous medium equation (WPME) and prove its convergence on bounded time intervals. This generalizes related work on blob methods for unweighted porous medium equations. From a numerical analysis perspective, our method has several advantages: it is meshfree, preserves the gradient flow structure of the underlying PDE, converges in arbitrary dimension, and captures the correct asymptotic behavior in simulations. That our method succeeds in capturing the long time behavior of WPME is significant from the perspective of related problems in quantization. Just as the Fokker-Planck equation provides a way to quantize a probability measure $\bar{\rho}$ by evolving an empirical measure according to stochastic Langevin dynamics so that the empirical measure flows toward $\bar{\rho}$, our particle method provides a way to quantize $\bar{\rho}$ according to deterministic particle dynamics approximating WMPE. In this way, our method has natural applications to multi-agent coverage algorithms and sampling probability measures. A specific case of our method corresponds exactly to the mean-field dynamics of training a two-layer neural network for a radial basis function activation function. From this perspective, our convergence result shows that, in the over parametrized regime and as the variance of the radial basis functions goes to zero, the continuum limit is given by WPME. This generalizes previous results, which considered the case of a uniform data distribution, to the more general inhomogeneous setting. As a consequence of our convergence result, we identify conditions on the target function and data distribution for which convexity of the energy landscape emerges in the continuum limit.

Multi-Robot Target Search using Probabilistic Consensus on Discrete Markov Chains

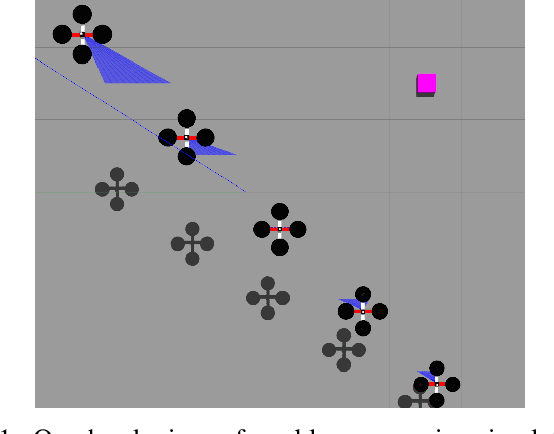
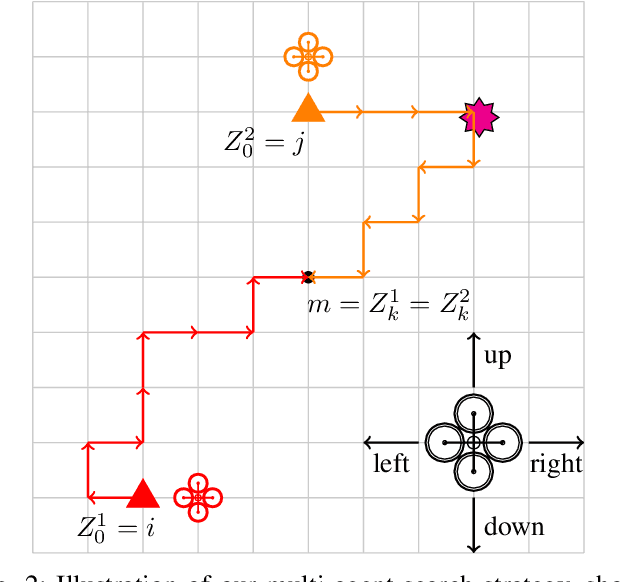
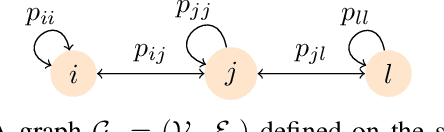
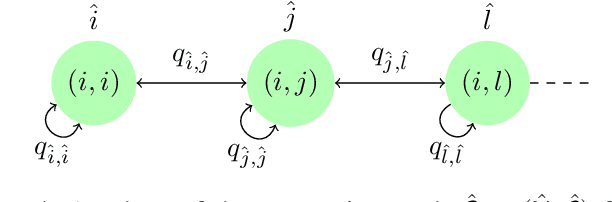
In this paper, we propose a probabilistic consensus-based multi-robot search strategy that is robust to communication link failures, and thus is suitable for disaster affected areas. The robots, capable of only local communication, explore a bounded environment according to a random walk modeled by a discrete-time discrete-state (DTDS) Markov chain and exchange information with neighboring robots, resulting in a time-varying communication network topology. The proposed strategy is proved to achieve consensus, here defined as agreement on the presence of a static target, with no assumptions on the connectivity of the communication network. Using numerical simulations, we investigate the effect of the robot population size, domain size, and information uncertainty on the consensus time statistics under this scheme. We also validate our theoretical results with 3D physics-based simulations in Gazebo. The simulations demonstrate that all robots achieve consensus in finite time with the proposed search strategy over a range of robot densities in the environment.

Using Reinforcement Learning to Herd a Robotic Swarm to a Target Distribution

In this paper, we present a reinforcement learning approach to designing a control policy for a "leader'' agent that herds a swarm of "follower'' agents, via repulsive interactions, as quickly as possible to a target probability distribution over a strongly connected graph. The leader control policy is a function of the swarm distribution, which evolves over time according to a mean-field model in the form of an ordinary difference equation. The dependence of the policy on agent populations at each graph vertex, rather than on individual agent activity, simplifies the observations required by the leader and enables the control strategy to scale with the number of agents. Two Temporal-Difference learning algorithms, SARSA and Q-Learning, are used to generate the leader control policy based on the follower agent distribution and the leader's location on the graph. A simulation environment corresponding to a grid graph with 4 vertices was used to train and validate the control policies for follower agent populations ranging from 10 to 100. Finally, the control policies trained on 100 simulated agents were used to successfully redistribute a physical swarm of 10 small robots to a target distribution among 4 spatial regions.