A blob method for inhomogeneous diffusion with applications to multi-agent control and sampling
Paper and Code
Mar 09, 2022
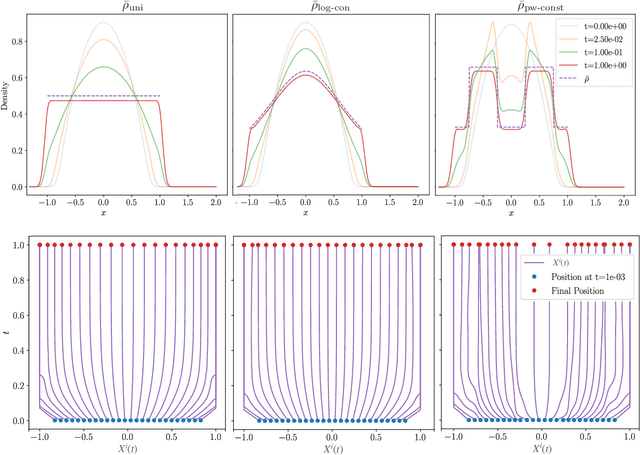


As a counterpoint to classical stochastic particle methods for linear diffusion equations, we develop a deterministic particle method for the weighted porous medium equation (WPME) and prove its convergence on bounded time intervals. This generalizes related work on blob methods for unweighted porous medium equations. From a numerical analysis perspective, our method has several advantages: it is meshfree, preserves the gradient flow structure of the underlying PDE, converges in arbitrary dimension, and captures the correct asymptotic behavior in simulations. That our method succeeds in capturing the long time behavior of WPME is significant from the perspective of related problems in quantization. Just as the Fokker-Planck equation provides a way to quantize a probability measure $\bar{\rho}$ by evolving an empirical measure according to stochastic Langevin dynamics so that the empirical measure flows toward $\bar{\rho}$, our particle method provides a way to quantize $\bar{\rho}$ according to deterministic particle dynamics approximating WMPE. In this way, our method has natural applications to multi-agent coverage algorithms and sampling probability measures. A specific case of our method corresponds exactly to the mean-field dynamics of training a two-layer neural network for a radial basis function activation function. From this perspective, our convergence result shows that, in the over parametrized regime and as the variance of the radial basis functions goes to zero, the continuum limit is given by WPME. This generalizes previous results, which considered the case of a uniform data distribution, to the more general inhomogeneous setting. As a consequence of our convergence result, we identify conditions on the target function and data distribution for which convexity of the energy landscape emerges in the continuum limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge