Score Matching Diffusion Based Feedback Control and Planning of Nonlinear Systems

We propose a novel control-theoretic framework that leverages principles from generative modeling -- specifically, Denoising Diffusion Probabilistic Models (DDPMs) -- to stabilize control-affine systems with nonholonomic constraints. Unlike traditional stochastic approaches, which rely on noise-driven dynamics in both forward and reverse processes, our method crucially eliminates the need for noise in the reverse phase, making it particularly relevant for control applications. We introduce two formulations: one where noise perturbs all state dimensions during the forward phase while the control system enforces time reversal deterministically, and another where noise is restricted to the control channels, embedding system constraints directly into the forward process. For controllable nonlinear drift-free systems, we prove that deterministic feedback laws can exactly reverse the forward process, ensuring that the system's probability density evolves correctly without requiring artificial diffusion in the reverse phase. Furthermore, for linear time-invariant systems, we establish a time-reversal result under the second formulation. By eliminating noise in the backward process, our approach provides a more practical alternative to machine learning-based denoising methods, which are unsuitable for control applications due to the presence of stochasticity. We validate our results through numerical simulations on benchmark systems, including a unicycle model in a domain with obstacles, a driftless five-dimensional system, and a four-dimensional linear system, demonstrating the potential for applying diffusion-inspired techniques in linear, nonlinear, and settings with state space constraints.

Dynamics-aware Diffusion Models for Planning and Control

This paper addresses the problem of generating dynamically admissible trajectories for control tasks using diffusion models, particularly in scenarios where the environment is complex and system dynamics are crucial for practical application. We propose a novel framework that integrates system dynamics directly into the diffusion model's denoising process through a sequential prediction and projection mechanism. This mechanism, aligned with the diffusion model's noising schedule, ensures generated trajectories are both consistent with expert demonstrations and adhere to underlying physical constraints. Notably, our approach can generate maximum likelihood trajectories and accurately recover trajectories generated by linear feedback controllers, even when explicit dynamics knowledge is unavailable. We validate the effectiveness of our method through experiments on standard control tasks and a complex non-convex optimal control problem involving waypoint tracking and collision avoidance, demonstrating its potential for efficient trajectory generation in practical applications.

Predicting AI Agent Behavior through Approximation of the Perron-Frobenius Operator

Predicting the behavior of AI-driven agents is particularly challenging without a preexisting model. In our paper, we address this by treating AI agents as nonlinear dynamical systems and adopting a probabilistic perspective to predict their statistical behavior using the Perron-Frobenius (PF) operator. We formulate the approximation of the PF operator as an entropy minimization problem, which can be solved by leveraging the Markovian property of the operator and decomposing its spectrum. Our data-driven methodology simultaneously approximates the PF operator to perform prediction of the evolution of the agents and also predicts the terminal probability density of AI agents, such as robotic systems and generative models. We demonstrate the effectiveness of our prediction model through extensive experiments on practical systems driven by AI algorithms.

Denoising Diffusion-Based Control of Nonlinear Systems

We propose a novel approach based on Denoising Diffusion Probabilistic Models (DDPMs) to control nonlinear dynamical systems. DDPMs are the state-of-art of generative models that have achieved success in a wide variety of sampling tasks. In our framework, we pose the feedback control problem as a generative task of drawing samples from a target set under control system constraints. The forward process of DDPMs constructs trajectories originating from a target set by adding noise. We learn to control a dynamical system in reverse such that the terminal state belongs to the target set. For control-affine systems without drift, we prove that the control system can exactly track the trajectory of the forward process in reverse, whenever the the Lie bracket based condition for controllability holds. We numerically study our approach on various nonlinear systems and verify our theoretical results. We also conduct numerical experiments for cases beyond our theoretical results on a physics-engine.

Noise in the reverse process improves the approximation capabilities of diffusion models

In Score based Generative Modeling (SGMs), the state-of-the-art in generative modeling, stochastic reverse processes are known to perform better than their deterministic counterparts. This paper delves into the heart of this phenomenon, comparing neural ordinary differential equations (ODEs) and neural stochastic differential equations (SDEs) as reverse processes. We use a control theoretic perspective by posing the approximation of the reverse process as a trajectory tracking problem. We analyze the ability of neural SDEs to approximate trajectories of the Fokker-Planck equation, revealing the advantages of stochasticity. First, neural SDEs exhibit a powerful regularizing effect, enabling $L^2$ norm trajectory approximation surpassing the Wasserstein metric approximation achieved by neural ODEs under similar conditions, even when the reference vector field or score function is not Lipschitz. Applying this result, we establish the class of distributions that can be sampled using score matching in SGMs, relaxing the Lipschitz requirement on the gradient of the data distribution in existing literature. Second, we show that this approximation property is preserved when network width is limited to the input dimension of the network. In this limited width case, the weights act as control inputs, framing our analysis as a controllability problem for neural SDEs in probability density space. This sheds light on how noise helps to steer the system towards the desired solution and illuminates the empirical success of stochasticity in generative modeling.

Fusing Multiple Algorithms for Heterogeneous Online Learning

This study addresses the challenge of online learning in contexts where agents accumulate disparate data, face resource constraints, and use different local algorithms. This paper introduces the Switched Online Learning Algorithm (SOLA), designed to solve the heterogeneous online learning problem by amalgamating updates from diverse agents through a dynamic switching mechanism contingent upon their respective performance and available resources. We theoretically analyze the design of the selecting mechanism to ensure that the regret of SOLA is bounded. Our findings show that the number of changes in selection needs to be bounded by a parameter dependent on the performance of the different local algorithms. Additionally, two test cases are presented to emphasize the effectiveness of SOLA, first on an online linear regression problem and then on an online classification problem with the MNIST dataset.

Astrocytes as a mechanism for meta-plasticity and contextually-guided network function

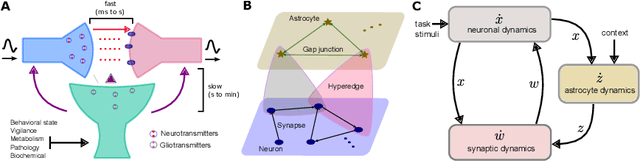
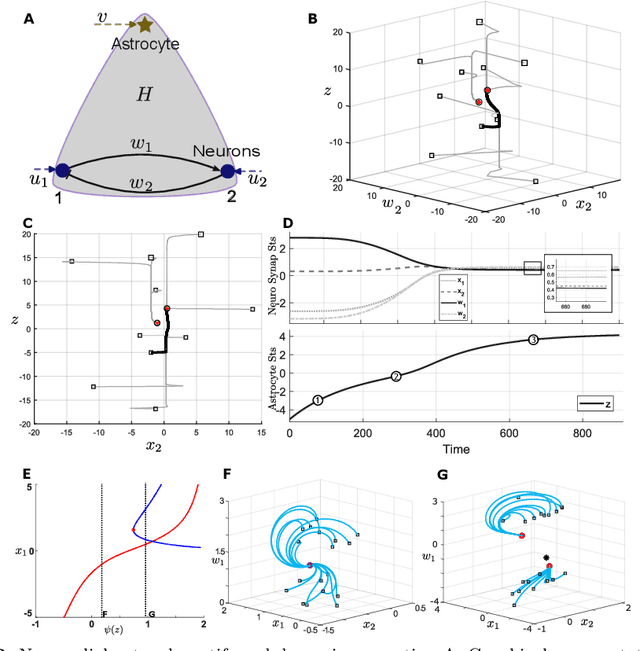
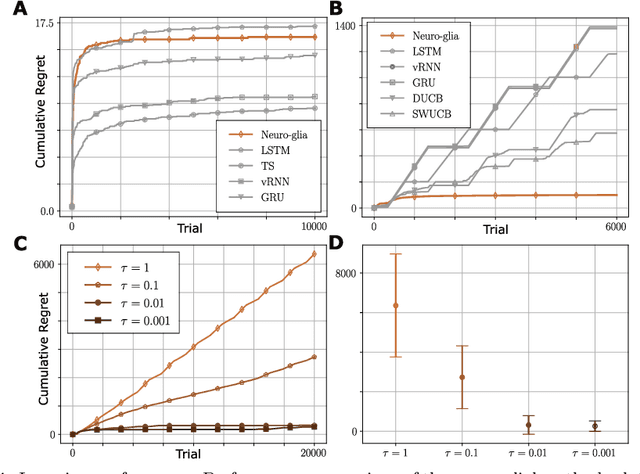
Astrocytes are a ubiquitous and enigmatic type of non-neuronal cell and are found in the brain of all vertebrates. While traditionally viewed as being supportive of neurons, it is increasingly recognized that astrocytes may play a more direct and active role in brain function and neural computation. On account of their sensitivity to a host of physiological covariates and ability to modulate neuronal activity and connectivity on slower time scales, astrocytes may be particularly well poised to modulate the dynamics of neural circuits in functionally salient ways. In the current paper, we seek to capture these features via actionable abstractions within computational models of neuron-astrocyte interaction. Specifically, we engage how nested feedback loops of neuron-astrocyte interaction, acting over separated time-scales may endow astrocytes with the capability to enable learning in context-dependent settings, where fluctuations in task parameters may occur much more slowly than within-task requirements. We pose a general model of neuron-synapse-astrocyte interaction and use formal analysis to characterize how astrocytic modulation may constitute a form of meta-plasticity, altering the ways in which synapses and neurons adapt as a function of time. We then embed this model in a bandit-based reinforcement learning task environment, and show how the presence of time-scale separated astrocytic modulation enables learning over multiple fluctuating contexts. Indeed, these networks learn far more reliably versus dynamically homogeneous networks and conventional non-network-based bandit algorithms. Our results indicate how the presence of neuron-astrocyte interaction in the brain may benefit learning over different time-scales and the conveyance of task-relevant contextual information onto circuit dynamics.

Learning on Manifolds: Universal Approximations Properties using Geometric Controllability Conditions for Neural ODEs

In numerous robotics and mechanical engineering applications, among others, data is often constrained on smooth manifolds due to the presence of rotational degrees of freedom. Common datadriven and learning-based methods such as neural ordinary differential equations (ODEs), however, typically fail to satisfy these manifold constraints and perform poorly for these applications. To address this shortcoming, in this paper we study a class of neural ordinary differential equations that, by design, leave a given manifold invariant, and characterize their properties by leveraging the controllability properties of control affine systems. In particular, using a result due to Agrachev and Caponigro on approximating diffeomorphisms with flows of feedback control systems, we show that any map that can be represented as the flow of a manifold-constrained dynamical system can also be approximated using the flow of manifold-constrained neural ODE, whenever a certain controllability condition is satisfied. Additionally, we show that this universal approximation property holds when the neural ODE has limited width in each layer, thus leveraging the depth of network instead for approximation. We verify our theoretical findings using numerical experiments on PyTorch for the manifolds S2 and the 3-dimensional orthogonal group SO(3), which are model manifolds for mechanical systems such as spacecrafts and satellites. We also compare the performance of the manifold invariant neural ODE with classical neural ODEs that ignore the manifold invariant properties and show the superiority of our approach in terms of accuracy and sample complexity.

Stochastic Contextual Bandits with Long Horizon Rewards

The growing interest in complex decision-making and language modeling problems highlights the importance of sample-efficient learning over very long horizons. This work takes a step in this direction by investigating contextual linear bandits where the current reward depends on at most $s$ prior actions and contexts (not necessarily consecutive), up to a time horizon of $h$. In order to avoid polynomial dependence on $h$, we propose new algorithms that leverage sparsity to discover the dependence pattern and arm parameters jointly. We consider both the data-poor ($T<h$) and data-rich ($T\ge h$) regimes, and derive respective regret upper bounds $\tilde O(d\sqrt{sT} +\min\{ q, T\})$ and $\tilde O(\sqrt{sdT})$, with sparsity $s$, feature dimension $d$, total time horizon $T$, and $q$ that is adaptive to the reward dependence pattern. Complementing upper bounds, we also show that learning over a single trajectory brings inherent challenges: While the dependence pattern and arm parameters form a rank-1 matrix, circulant matrices are not isometric over rank-1 manifolds and sample complexity indeed benefits from the sparse reward dependence structure. Our results necessitate a new analysis to address long-range temporal dependencies across data and avoid polynomial dependence on the reward horizon $h$. Specifically, we utilize connections to the restricted isometry property of circulant matrices formed by dependent sub-Gaussian vectors and establish new guarantees that are also of independent interest.

Representation Learning for Context-Dependent Decision-Making

Humans are capable of adjusting to changing environments flexibly and quickly. Empirical evidence has revealed that representation learning plays a crucial role in endowing humans with such a capability. Inspired by this observation, we study representation learning in the sequential decision-making scenario with contextual changes. We propose an online algorithm that is able to learn and transfer context-dependent representations and show that it significantly outperforms the existing ones that do not learn representations adaptively. As a case study, we apply our algorithm to the Wisconsin Card Sorting Task, a well-established test for the mental flexibility of humans in sequential decision-making. By comparing our algorithm with the standard Q-learning and Deep-Q learning algorithms, we demonstrate the benefits of adaptive representation learning.