Weyl Calculus and Exactly Solvable Schrödinger Bridges with Quadratic State Cost

Schr\"{o}dinger bridge--a stochastic dynamical generalization of optimal mass transport--exhibits a learning-control duality. Viewed as a stochastic control problem, the Schr\"{o}dinger bridge finds an optimal control policy that steers a given joint state statistics to another while minimizing the total control effort subject to controlled diffusion and deadline constraints. Viewed as a stochastic learning problem, the Schr\"{o}dinger bridge finds the most-likely distribution-valued trajectory connecting endpoint distributional observations, i.e., solves the two point boundary-constrained maximum likelihood problem over the manifold of probability distributions. Recent works have shown that solving the Schr\"{o}dinger bridge problem with state cost requires finding the Markov kernel associated with a reaction-diffusion PDE where the state cost appears as a state-dependent reaction rate. We explain how ideas from Weyl calculus in quantum mechanics, specifically the Weyl operator and the Weyl symbol, can help determine such Markov kernels. We illustrate these ideas by explicitly finding the Markov kernel for the case of quadratic state cost via Weyl calculus, recovering our earlier results but avoiding tedious computation with Hermite polynomials.

Schrödinger Bridge with Quadratic State Cost is Exactly Solvable

Schr\"odinger bridge is a diffusion process that steers a given distribution to another in a prescribed time while minimizing the effort to do so. It can be seen as the stochastic dynamical version of the optimal mass transport, and has growing applications in generative diffusion models and stochastic optimal control. In this work, we propose a regularized variant of the Schr\"odinger bridge with a quadratic state cost-to-go that incentivizes the optimal sample paths to stay close to a nominal level. Unlike the conventional Schr\"odinger bridge, the regularization induces a state-dependent rate of killing and creation of probability mass, and its solution requires determining the Markov kernel of a reaction-diffusion partial differential equation. We derive this Markov kernel in closed form. Our solution recovers the heat kernel in the vanishing regularization (i.e., diffusion without reaction) limit, thereby recovering the solution of the conventional Schr\"odinger bridge. Our results enable the use of dynamic Sinkhorn recursion for computing the Schr\"odinger bridge with a quadratic state cost-to-go, which would otherwise be challenging to use in this setting. We deduce properties of the new kernel and explain its connections with certain exactly solvable models in quantum mechanics.

Stochastic Learning of Computational Resource Usage as Graph Structured Multimarginal Schrödinger Bridge

We propose to learn the time-varying stochastic computational resource usage of software as a graph structured Schr\"odinger bridge problem. In general, learning the computational resource usage from data is challenging because resources such as the number of CPU instructions and the number of last level cache requests are both time-varying and statistically correlated. Our proposed method enables learning the joint time-varying stochasticity in computational resource usage from the measured profile snapshots in a nonparametric manner. The method can be used to predict the most-likely time-varying distribution of computational resource availability at a desired time. We provide detailed algorithms for stochastic learning in both single and multi-core cases, discuss the convergence guarantees, computational complexities, and demonstrate their practical use in two case studies: a single-core nonlinear model predictive controller, and a synthetic multi-core software.

Solution of the Probabilistic Lambert Problem: Connections with Optimal Mass Transport, Schrödinger Bridge and Reaction-Diffusion PDEs

Lambert's problem concerns with transferring a spacecraft from a given initial to a given terminal position within prescribed flight time via velocity control subject to a gravitational force field. We consider a probabilistic variant of the Lambert problem where the knowledge of the endpoint constraints in position vectors are replaced by the knowledge of their respective joint probability density functions. We show that the Lambert problem with endpoint joint probability density constraints is a generalized optimal mass transport (OMT) problem, thereby connecting this classical astrodynamics problem with a burgeoning area of research in modern stochastic control and stochastic machine learning. This newfound connection allows us to rigorously establish the existence and uniqueness of solution for the probabilistic Lambert problem. The same connection also helps to numerically solve the probabilistic Lambert problem via diffusion regularization, i.e., by leveraging further connection of the OMT with the Schr\"odinger bridge problem (SBP). This also shows that the probabilistic Lambert problem with additive dynamic process noise is in fact a generalized SBP, and can be solved numerically using the so-called Schr\"odinger factors, as we do in this work. We explain how the resulting analysis leads to solving a boundary-coupled system of reaction-diffusion PDEs where the nonlinear gravitational potential appears as the reaction rate. We propose novel algorithms for the same, and present illustrative numerical results. Our analysis and the algorithmic framework are nonparametric, i.e., we make neither statistical (e.g., Gaussian, first few moments, mixture or exponential family, finite dimensionality of the sufficient statistic) nor dynamical (e.g., Taylor series) approximations.

Path Structured Multimarginal Schrödinger Bridge for Probabilistic Learning of Hardware Resource Usage by Control Software

The solution of the path structured multimarginal Schr\"{o}dinger bridge problem (MSBP) is the most-likely measure-valued trajectory consistent with a sequence of observed probability measures or distributional snapshots. We leverage recent algorithmic advances in solving such structured MSBPs for learning stochastic hardware resource usage by control software. The solution enables predicting the time-varying distribution of hardware resource availability at a desired time with guaranteed linear convergence. We demonstrate the efficacy of our probabilistic learning approach in a model predictive control software execution case study. The method exhibits rapid convergence to an accurate prediction of hardware resource utilization of the controller. The method can be broadly applied to any software to predict cyber-physical context-dependent performance at arbitrary time.

On the Contraction Coefficient of the Schrödinger Bridge for Stochastic Linear Systems

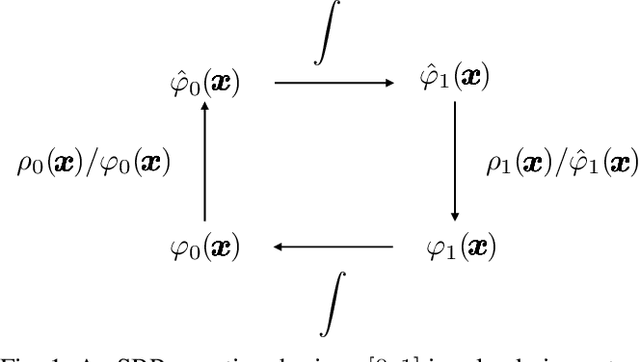
Schr\"{o}dinger bridge is a stochastic optimal control problem to steer a given initial state density to another, subject to controlled diffusion and deadline constraints. A popular method to numerically solve the Schr\"{o}dinger bridge problems, in both classical and in the linear system settings, is via contractive fixed point recursions. These recursions can be seen as dynamic versions of the well-known Sinkhorn iterations, and under mild assumptions, they solve the so-called Schr\"{o}dinger systems with guaranteed linear convergence. In this work, we study a priori estimates for the contraction coefficients associated with the convergence of respective Schr\"{o}dinger systems. We provide new geometric and control-theoretic interpretations for the same. Building on these newfound interpretations, we point out the possibility of improved computation for the worst-case contraction coefficients of linear SBPs by preconditioning the endpoint support sets.

Neural Schrödinger Bridge with Sinkhorn Losses: Application to Data-driven Minimum Effort Control of Colloidal Self-assembly

We show that the minimum effort control of colloidal self-assembly can be naturally formulated in the order-parameter space as a generalized Schr\"odinger bridge problem -- a class of fixed-horizon stochastic optimal control problems that originated in the works of Erwin Schr\"odinger in the early 1930s. In recent years, this class of problems has seen a resurgence of research activities in control and machine learning communities. Different from the existing literature on the theory and computation for such problems, the controlled drift and diffusion coefficients for colloidal self-assembly are typically non-affine in control, and are difficult to obtain from physics-based modeling. We deduce the conditions of optimality for such generalized problems, and show that the resulting system of equations is structurally very different from the existing results in a way that standard computational approaches no longer apply. Thus motivated, we propose a data-driven learning and control framework, named `neural Schr\"odinger bridge', to solve such generalized Schr\"odinger bridge problems by innovating on recent advances in neural networks. We illustrate the effectiveness of the proposed framework using a numerical case study of colloidal self-assembly. We learn the controlled drift and diffusion coefficients as two neural networks using molecular dynamics simulation data, and then use these two to train a third network with Sinkhorn losses designed for distributional endpoint constraints, specific for this class of control problems.

Optimal Mass Transport over the Euler Equation

We consider the finite horizon optimal steering of the joint state probability distribution subject to the angular velocity dynamics governed by the Euler equation. The problem and its solution amounts to controlling the spin of a rigid body via feedback, and is of practical importance, for example, in angular stabilization of a spacecraft with stochastic initial and terminal states. We clarify how this problem is an instance of the optimal mass transport (OMT) problem with bilinear prior drift. We deduce both static and dynamic versions of the Eulerian OMT, and provide analytical and numerical results for the synthesis of the optimal controller.

Proximal Mean Field Learning in Shallow Neural Networks

Recent mean field interpretations of learning dynamics in over-parameterized neural networks offer theoretical insights on the empirical success of first order optimization algorithms in finding global minima of the nonconvex risk landscape. In this paper, we explore applying mean field learning dynamics as a computational algorithm, rather than as an analytical tool. Specifically, we design a Sinkhorn regularized proximal algorithm to approximate the distributional flow from the learning dynamics in the mean field regime over weighted point clouds. In this setting, a contractive fixed point recursion computes the time-varying weights, numerically realizing the interacting Wasserstein gradient flow of the parameter distribution supported over the neuronal ensemble. An appealing aspect of the proposed algorithm is that the measure-valued recursions allow meshless computation. We demonstrate the proposed computational framework of interacting weighted particle evolution on binary and multi-class classification. Our algorithm performs gradient descent of the free energy associated with the risk functional.

Convex and Nonconvex Sublinear Regression with Application to Data-driven Learning of Reach Sets

We consider estimating a compact set from finite data by approximating the support function of that set via sublinear regression. Support functions uniquely characterize a compact set up to closure of convexification, and are sublinear (convex as well as positive homogeneous of degree one). Conversely, any sublinear function is the support function of a compact set. We leverage this property to transcribe the task of learning a compact set to that of learning its support function. We propose two algorithms to perform the sublinear regression, one via convex and another via nonconvex programming. The convex programming approach involves solving a quadratic program (QP) followed by a linear program (LP), and is referred to as QP-LP. The nonconvex programming approach involves training a input sublinear neural network. We illustrate the proposed methods via numerical examples on learning the reach sets of controlled dynamics subject to set-valued input uncertainties from trajectory data.