A Unifying Generator Loss Function for Generative Adversarial Networks

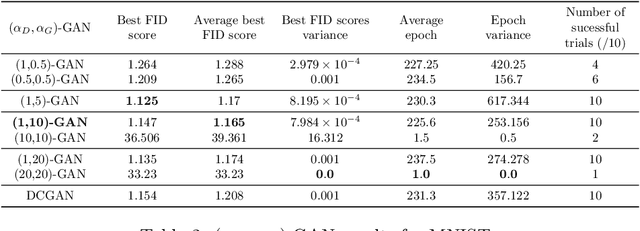
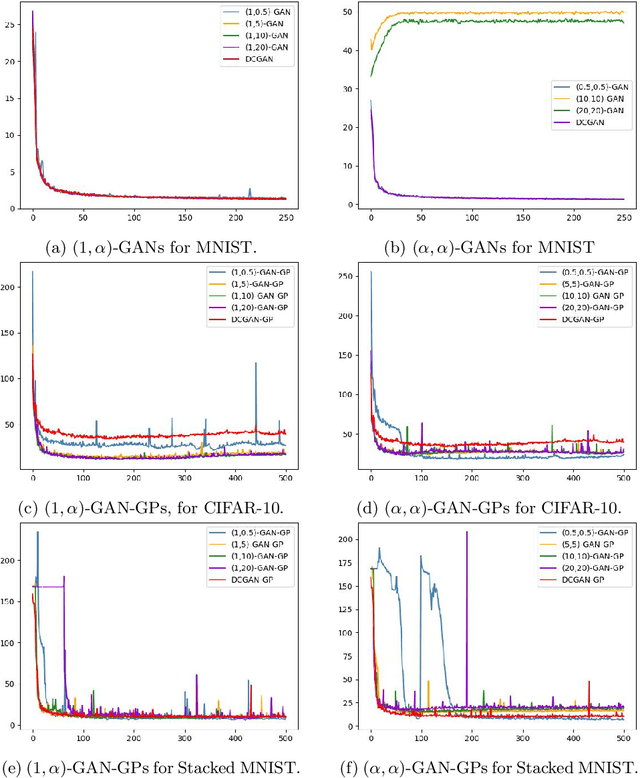
A unifying $\alpha$-parametrized generator loss function is introduced for a dual-objective generative adversarial network (GAN), which uses a canonical (or classical) discriminator loss function such as the one in the original GAN (VanillaGAN) system. The generator loss function is based on a symmetric class probability estimation type function, $\mathcal{L}_\alpha$, and the resulting GAN system is termed $\mathcal{L}_\alpha$-GAN. Under an optimal discriminator, it is shown that the generator's optimization problem consists of minimizing a Jensen-$f_\alpha$-divergence, a natural generalization of the Jensen-Shannon divergence, where $f_\alpha$ is a convex function expressed in terms of the loss function $\mathcal{L}_\alpha$. It is also demonstrated that this $\mathcal{L}_\alpha$-GAN problem recovers as special cases a number of GAN problems in the literature, including VanillaGAN, Least Squares GAN (LSGAN), Least $k$th order GAN (L$k$GAN) and the recently introduced $(\alpha_D,\alpha_G)$-GAN with $\alpha_D=1$. Finally, experimental results are conducted on three datasets, MNIST, CIFAR-10, and Stacked MNIST to illustrate the performance of various examples of the $\mathcal{L}_\alpha$-GAN system.

Evaluating Trade-offs in Computer Vision Between Attribute Privacy, Fairness and Utility

This paper investigates to what degree and magnitude tradeoffs exist between utility, fairness and attribute privacy in computer vision. Regarding privacy, we look at this important problem specifically in the context of attribute inference attacks, a less addressed form of privacy. To create a variety of models with different preferences, we use adversarial methods to intervene on attributes relating to fairness and privacy. We see that that certain tradeoffs exist between fairness and utility, privacy and utility, and between privacy and fairness. The results also show that those tradeoffs and interactions are more complex and nonlinear between the three goals than intuition would suggest.

On the Rényi Cross-Entropy

The R\'{e}nyi cross-entropy measure between two distributions, a generalization of the Shannon cross-entropy, was recently used as a loss function for the improved design of deep learning generative adversarial networks. In this work, we examine the properties of this measure and derive closed-form expressions for it when one of the distributions is fixed and when both distributions belong to the exponential family. We also analytically determine a formula for the cross-entropy rate for stationary Gaussian processes and for finite-alphabet Markov sources.

Achieving Utility, Fairness, and Compactness via Tunable Information Bottleneck Measures

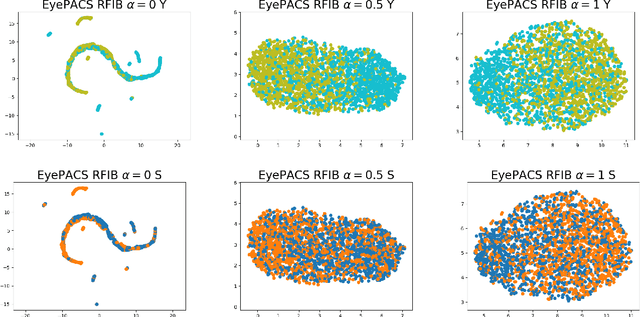
Designing machine learning algorithms that are accurate yet fair, not discriminating based on any sensitive attribute, is of paramount importance for society to accept AI for critical applications. In this article, we propose a novel fair representation learning method termed the R\'enyi Fair Information Bottleneck Method (RFIB) which incorporates constraints for utility, fairness, and compactness of representation, and apply it to image classification. A key attribute of our approach is that we consider - in contrast to most prior work - both demographic parity and equalized odds as fairness constraints, allowing for a more nuanced satisfaction of both criteria. Leveraging a variational approach, we show that our objectives yield a loss function involving classical Information Bottleneck (IB) measures and establish an upper bound in terms of the R\'enyi divergence of order $\alpha$ on the mutual information IB term measuring compactness between the input and its encoded embedding. Experimenting on three different image datasets (EyePACS, CelebA, and FairFace), we study the influence of the $\alpha$ parameter as well as two other tunable IB parameters on achieving utility/fairness trade-off goals, and show that the $\alpha$ parameter gives an additional degree of freedom that can be used to control the compactness of the representation. We evaluate the performance of our method using various utility, fairness, and compound utility/fairness metrics, showing that RFIB outperforms current state-of-the-art approaches.

Renyi Fair Information Bottleneck for Image Classification

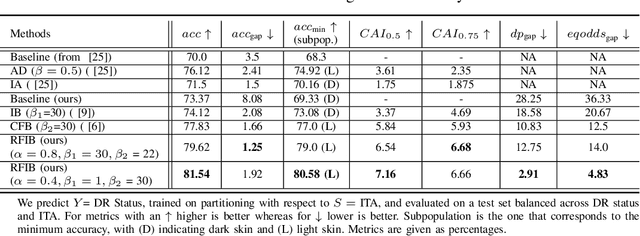
We develop a novel method for ensuring fairness in machine learning which we term as the Renyi Fair Information Bottleneck (RFIB). We consider two different fairness constraints - demographic parity and equalized odds - for learning fair representations and derive a loss function via a variational approach that uses Renyi's divergence with its tunable parameter $\alpha$ and that takes into account the triple constraints of utility, fairness, and compactness of representation. We then evaluate the performance of our method for image classification using the EyePACS medical imaging dataset, showing it outperforms competing state of the art techniques with performance measured using a variety of compound utility/fairness metrics, including accuracy gap and Rawls' minimal accuracy.

Rényi Generative Adversarial Networks

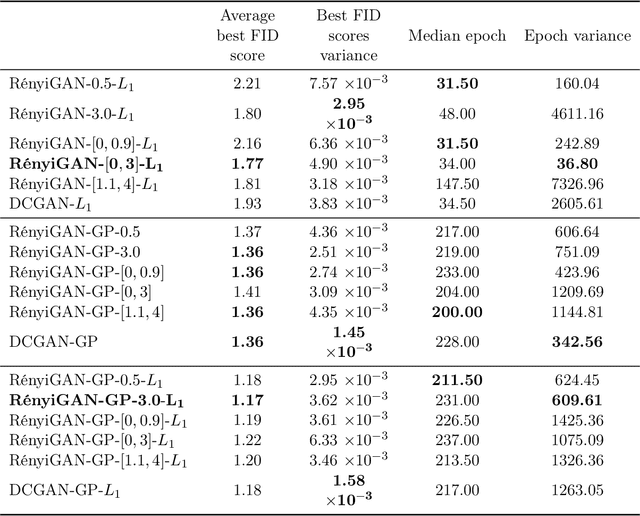
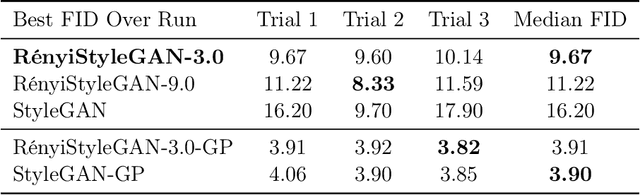
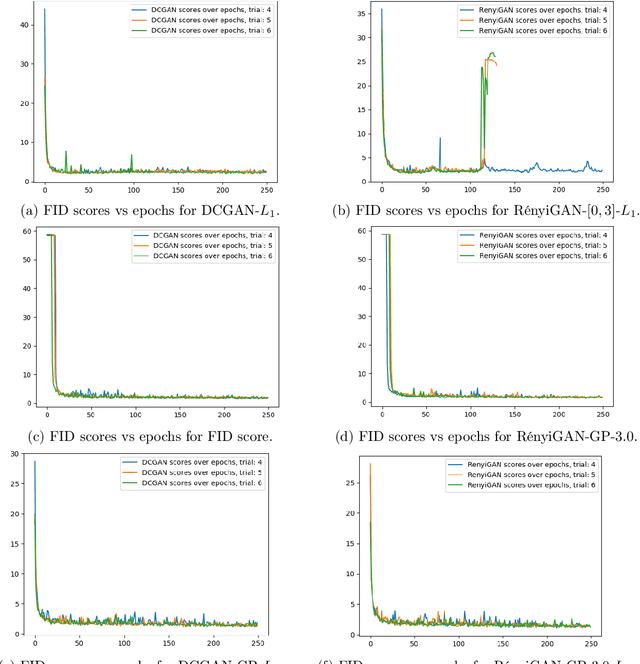
We propose a loss function for generative adversarial networks (GANs) using R\'{e}nyi information measures with parameter $\alpha$. More specifically, we formulate GAN's generator loss function in terms of R\'{e}nyi cross-entropy functionals. We demonstrate that for any $\alpha$, this generalized loss function preserves the equilibrium point satisfied by the original GAN loss based on the Jensen-Renyi divergence, a natural extension of the Jensen-Shannon divergence. We also prove that the R\'{e}nyi-centric loss function reduces to the original GAN loss function as $\alpha \to 1$. We show empirically that the proposed loss function, when implemented on both DCGAN (with $L_1$ normalization) and StyleGAN architectures, confers performance benefits by virtue of the extra degree of freedom provided by the parameter $\alpha$. More specifically, we show improvements with regard to: (a) the quality of the generated images as measured via the Fr\'echet Inception Distance (FID) score (e.g., best FID=8.33 for RenyiStyleGAN vs 9.7 for StyleGAN when evaluated over 64$\times$64 CelebA images) and (b) training stability. While it was applied to GANs in this study, the proposed approach is generic and can be used in other applications of information theory to deep learning, e.g., AI bias or privacy.

Unsupervised Semantic Attribute Discovery and Control in Generative Models

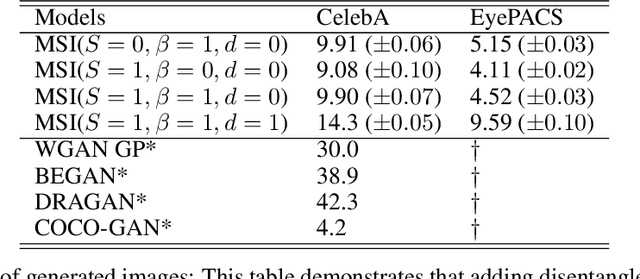
This work focuses on the ability to control via latent space factors semantic image attributes in generative models, and the faculty to discover mappings from factors to attributes in an unsupervised fashion. The discovery of controllable semantic attributes is of special importance, as it would facilitate higher level tasks such as unsupervised representation learning to improve anomaly detection, or the controlled generation of novel data for domain shift and imbalanced datasets. The ability to control semantic attributes is related to the disentanglement of latent factors, which dictates that latent factors be "uncorrelated" in their effects. Unfortunately, despite past progress, the connection between control and disentanglement remains, at best, confused and entangled, requiring clarifications we hope to provide in this work. To this end, we study the design of algorithms for image generation that allow unsupervised discovery and control of semantic attributes.We make several contributions: a) We bring order to the concepts of control and disentanglement, by providing an analytical derivation that connects mutual information maximization, which promotes attribute control, to total correlation minimization, which relates to disentanglement. b) We propose hybrid generative model architectures that use mutual information maximization with multi-scale style transfer. c) We introduce a novel metric to characterize the performance of semantic attributes control. We report experiments that appear to demonstrate, quantitatively and qualitatively, the ability of the proposed model to perform satisfactory control while still preserving competitive visual quality. We compare to other state of the art methods (e.g., Frechet inception distance (FID)= 9.90 on CelebA and 4.52 on EyePACS).

Information Extraction Under Privacy Constraints

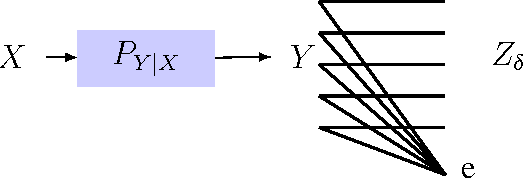
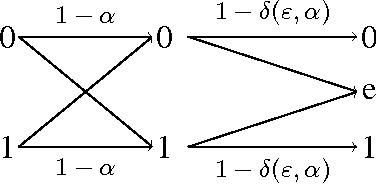
A privacy-constrained information extraction problem is considered where for a pair of correlated discrete random variables $(X,Y)$ governed by a given joint distribution, an agent observes $Y$ and wants to convey to a potentially public user as much information about $Y$ as possible without compromising the amount of information revealed about $X$. To this end, the so-called {\em rate-privacy function} is introduced to quantify the maximal amount of information (measured in terms of mutual information) that can be extracted from $Y$ under a privacy constraint between $X$ and the extracted information, where privacy is measured using either mutual information or maximal correlation. Properties of the rate-privacy function are analyzed and information-theoretic and estimation-theoretic interpretations of it are presented for both the mutual information and maximal correlation privacy measures. It is also shown that the rate-privacy function admits a closed-form expression for a large family of joint distributions of $(X,Y)$. Finally, the rate-privacy function under the mutual information privacy measure is considered for the case where $(X,Y)$ has a joint probability density function by studying the problem where the extracted information is a uniform quantization of $Y$ corrupted by additive Gaussian noise. The asymptotic behavior of the rate-privacy function is studied as the quantization resolution grows without bound and it is observed that not all of the properties of the rate-privacy function carry over from the discrete to the continuous case.