Bounds on the Excess Minimum Risk via Generalized Information Divergence Measures

Given finite-dimensional random vectors $Y$, $X$, and $Z$ that form a Markov chain in that order (i.e., $Y \to X \to Z$), we derive upper bounds on the excess minimum risk using generalized information divergence measures. Here, $Y$ is a target vector to be estimated from an observed feature vector $X$ or its stochastically degraded version $Z$. The excess minimum risk is defined as the difference between the minimum expected loss in estimating $Y$ from $X$ and from $Z$. We present a family of bounds that generalize the mutual information based bound of Gy\"orfi et al. (2023), using the R\'enyi and $\alpha$-Jensen-Shannon divergences, as well as Sibson's mutual information. Our bounds are similar to those developed by Modak et al. (2021) and Aminian et al. (2024) for the generalization error of learning algorithms. However, unlike these works, our bounds do not require the sub-Gaussian parameter to be constant and therefore apply to a broader class of joint distributions over $Y$, $X$, and $Z$. We also provide numerical examples under both constant and non-constant sub-Gaussianity assumptions, illustrating that our generalized divergence based bounds can be tighter than the one based on mutual information for certain regimes of the parameter $\alpha$.

Lossless Transformations and Excess Risk Bounds in Statistical Inference

We study the excess minimum risk in statistical inference, defined as the difference between the minimum expected loss in estimating a random variable from an observed feature vector and the minimum expected loss in estimating the same random variable from a transformation (statistic) of the feature vector. After characterizing lossless transformations, i.e., transformations for which the excess risk is zero for all loss functions, we construct a partitioning test statistic for the hypothesis that a given transformation is lossless and show that for i.i.d. data the test is strongly consistent. More generally, we develop information-theoretic upper bounds on the excess risk that uniformly hold over fairly general classes of loss functions. Based on these bounds, we introduce the notion of a delta-lossless transformation and give sufficient conditions for a given transformation to be universally delta-lossless. Applications to classification, nonparametric regression, portfolio strategies, information bottleneck, and deep learning, are also surveyed.

On the Rényi Cross-Entropy

The R\'{e}nyi cross-entropy measure between two distributions, a generalization of the Shannon cross-entropy, was recently used as a loss function for the improved design of deep learning generative adversarial networks. In this work, we examine the properties of this measure and derive closed-form expressions for it when one of the distributions is fixed and when both distributions belong to the exponential family. We also analytically determine a formula for the cross-entropy rate for stationary Gaussian processes and for finite-alphabet Markov sources.

Information Extraction Under Privacy Constraints

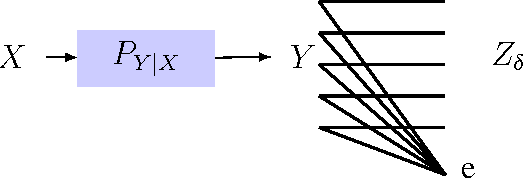
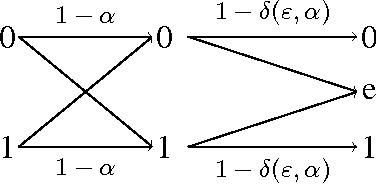
A privacy-constrained information extraction problem is considered where for a pair of correlated discrete random variables $(X,Y)$ governed by a given joint distribution, an agent observes $Y$ and wants to convey to a potentially public user as much information about $Y$ as possible without compromising the amount of information revealed about $X$. To this end, the so-called {\em rate-privacy function} is introduced to quantify the maximal amount of information (measured in terms of mutual information) that can be extracted from $Y$ under a privacy constraint between $X$ and the extracted information, where privacy is measured using either mutual information or maximal correlation. Properties of the rate-privacy function are analyzed and information-theoretic and estimation-theoretic interpretations of it are presented for both the mutual information and maximal correlation privacy measures. It is also shown that the rate-privacy function admits a closed-form expression for a large family of joint distributions of $(X,Y)$. Finally, the rate-privacy function under the mutual information privacy measure is considered for the case where $(X,Y)$ has a joint probability density function by studying the problem where the extracted information is a uniform quantization of $Y$ corrupted by additive Gaussian noise. The asymptotic behavior of the rate-privacy function is studied as the quantization resolution grows without bound and it is observed that not all of the properties of the rate-privacy function carry over from the discrete to the continuous case.

Efficient Tracking of Large Classes of Experts

In the framework of prediction of individual sequences, sequential prediction methods are to be constructed that perform nearly as well as the best expert from a given class. We consider prediction strategies that compete with the class of switching strategies that can segment a given sequence into several blocks, and follow the advice of a different "base" expert in each block. As usual, the performance of the algorithm is measured by the regret defined as the excess loss relative to the best switching strategy selected in hindsight for the particular sequence to be predicted. In this paper we construct prediction strategies of low computational cost for the case where the set of base experts is large. In particular we provide a method that can transform any prediction algorithm $\A$ that is designed for the base class into a tracking algorithm. The resulting tracking algorithm can take advantage of the prediction performance and potential computational efficiency of $\A$ in the sense that it can be implemented with time and space complexity only $O(n^{\gamma} \ln n)$ times larger than that of $\A$, where $n$ is the time horizon and $\gamma \ge 0$ is a parameter of the algorithm. With $\A$ properly chosen, our algorithm achieves a regret bound of optimal order for $\gamma>0$, and only $O(\ln n)$ times larger than the optimal order for $\gamma=0$ for all typical regret bound types we examined. For example, for predicting binary sequences with switching parameters under the logarithmic loss, our method achieves the optimal $O(\ln n)$ regret rate with time complexity $O(n^{1+\gamma}\ln n)$ for any $\gamma\in (0,1)$.