Computational Efficiency under Covariate Shift in Kernel Ridge Regression

This paper addresses the covariate shift problem in the context of nonparametric regression within reproducing kernel Hilbert spaces (RKHSs). Covariate shift arises in supervised learning when the input distributions of the training and test data differ, presenting additional challenges for learning. Although kernel methods have optimal statistical properties, their high computational demands in terms of time and, particularly, memory, limit their scalability to large datasets. To address this limitation, the main focus of this paper is to explore the trade-off between computational efficiency and statistical accuracy under covariate shift. We investigate the use of random projections where the hypothesis space consists of a random subspace within a given RKHS. Our results show that, even in the presence of covariate shift, significant computational savings can be achieved without compromising learning performance.

A model for efficient dynamical ranking in networks

We present a physics-inspired method for inferring dynamic rankings in directed temporal networks - networks in which each directed and timestamped edge reflects the outcome and timing of a pairwise interaction. The inferred ranking of each node is real-valued and varies in time as each new edge, encoding an outcome like a win or loss, raises or lowers the node's estimated strength or prestige, as is often observed in real scenarios including sequences of games, tournaments, or interactions in animal hierarchies. Our method works by solving a linear system of equations and requires only one parameter to be tuned. As a result, the corresponding algorithm is scalable and efficient. We test our method by evaluating its ability to predict interactions (edges' existence) and their outcomes (edges' directions) in a variety of applications, including both synthetic and real data. Our analysis shows that in many cases our method's performance is better than existing methods for predicting dynamic rankings and interaction outcomes.

Snacks: a fast large-scale kernel SVM solver

Kernel methods provide a powerful framework for non parametric learning. They are based on kernel functions and allow learning in a rich functional space while applying linear statistical learning tools, such as Ridge Regression or Support Vector Machines. However, standard kernel methods suffer from a quadratic time and memory complexity in the number of data points and thus have limited applications in large-scale learning. In this paper, we propose Snacks, a new large-scale solver for Kernel Support Vector Machines. Specifically, Snacks relies on a Nystr\"om approximation of the kernel matrix and an accelerated variant of the stochastic subgradient method. We demonstrate formally through a detailed empirical evaluation, that it competes with other SVM solvers on a variety of benchmark datasets.

Regularized ERM on random subspaces

We study a natural extension of classical empirical risk minimization, where the hypothesis space is a random subspace of a given space. In particular, we consider possibly data dependent subspaces spanned by a random subset of the data, recovering as a special case Nystrom approaches for kernel methods. Considering random subspaces naturally leads to computational savings, but the question is whether the corresponding learning accuracy is degraded. These statistical-computational tradeoffs have been recently explored for the least squares loss and self-concordant loss functions, such as the logistic loss. Here, we work to extend these results to convex Lipschitz loss functions, that might not be smooth, such as the hinge loss used in support vector machines. This unified analysis requires developing new proofs, that use different technical tools, such as sub-gaussian inputs, to achieve fast rates. Our main results show the existence of different settings, depending on how hard the learning problem is, for which computational efficiency can be improved with no loss in performance.

AdaTask: Adaptive Multitask Online Learning

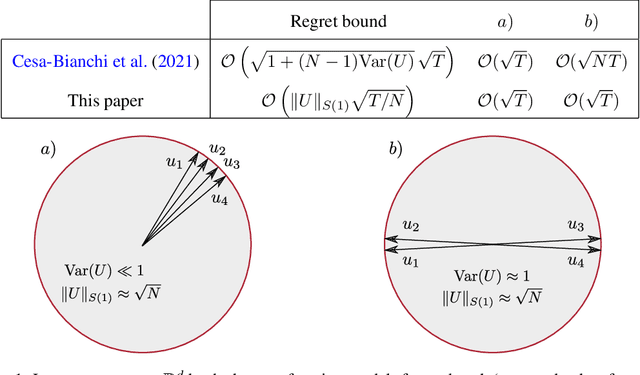
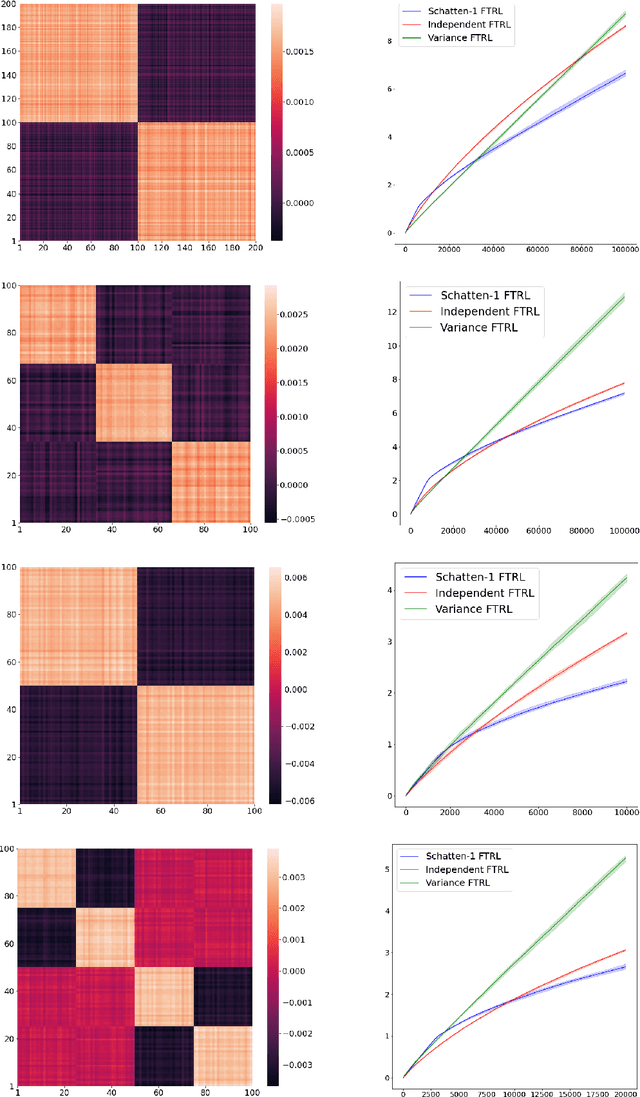
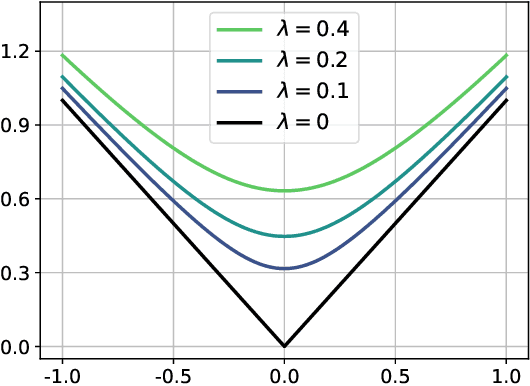
We introduce and analyze AdaTask, a multitask online learning algorithm that adapts to the unknown structure of the tasks. When the $N$ tasks are stochastically activated, we show that the regret of AdaTask is better, by a factor that can be as large as $\sqrt{N}$, than the regret achieved by running $N$ independent algorithms, one for each task. AdaTask can be seen as a comparator-adaptive version of Follow-the-Regularized-Leader with a Mahalanobis norm potential. Through a variational formulation of this potential, our analysis reveals how AdaTask jointly learns the tasks and their structure. Experiments supporting our findings are presented.