To Each Optimizer a Norm, To Each Norm its Generalization

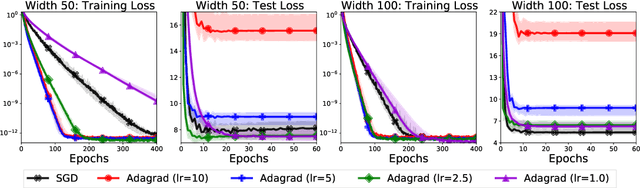
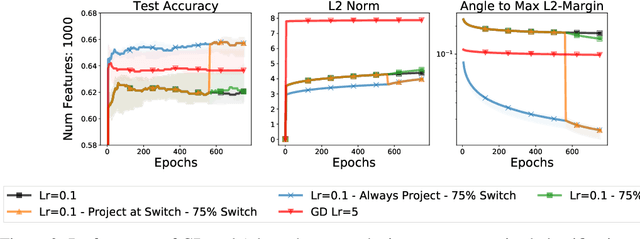
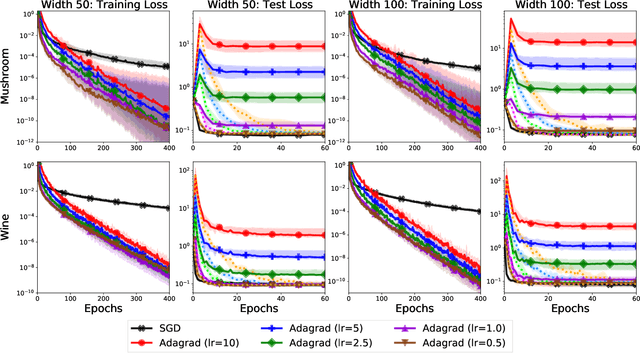
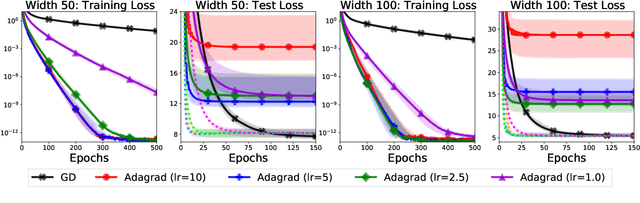
We study the implicit regularization of optimization methods for linear models interpolating the training data in the under-parametrized and over-parametrized regimes. Since it is difficult to determine whether an optimizer converges to solutions that minimize a known norm, we flip the problem and investigate what is the corresponding norm minimized by an interpolating solution. Using this reasoning, we prove that for over-parameterized linear regression, projections onto linear spans can be used to move between different interpolating solutions. For under-parameterized linear classification, we prove that for any linear classifier separating the data, there exists a family of quadratic norms ||.||_P such that the classifier's direction is the same as that of the maximum P-margin solution. For linear classification, we argue that analyzing convergence to the standard maximum l2-margin is arbitrary and show that minimizing the norm induced by the data results in better generalization. Furthermore, for over-parameterized linear classification, projections onto the data-span enable us to use techniques from the under-parameterized setting. On the empirical side, we propose techniques to bias optimizers towards better generalizing solutions, improving their test performance. We validate our theoretical results via synthetic experiments, and use the neural tangent kernel to handle non-linear models.

GEAR: Geometry-Aware Rényi Information

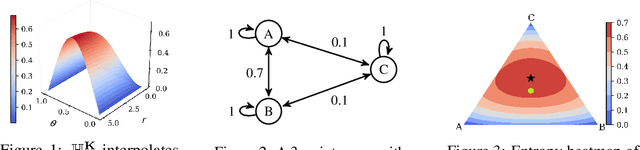
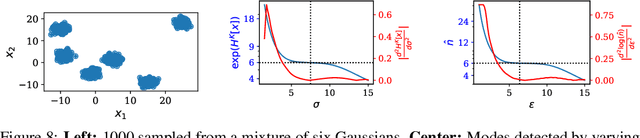
Shannon's seminal theory of information has been of paramount importance in the development of modern machine learning techniques. However, standard information measures deal with probability distributions over an alphabet considered as a mere set of symbols and disregard further geometric structure, which might be available in the form of a metric or similarity function. We advocate the use of a notion of entropy that reflects not only the relative abundances of symbols but also the similarities between them, which was originally introduced in theoretical ecology to study the diversity of biological communities. Echoing this idea, we propose a criterion for comparing two probability distributions (possibly degenerate and with non-overlapping supports) that takes into account the geometry of the space in which the distributions are defined. Our proposal exhibits performance on par with state-of-the-art methods based on entropy-regularized optimal transport, but enjoys a closed-form expression and thus a lower computational cost. We demonstrate the versatility of our proposal via experiments on a broad range of domains: computing image barycenters, approximating densities with a collection of (super-) samples; summarizing texts; assessing mode coverage; as well as training generative models.

Beyond Local Nash Equilibria for Adversarial Networks

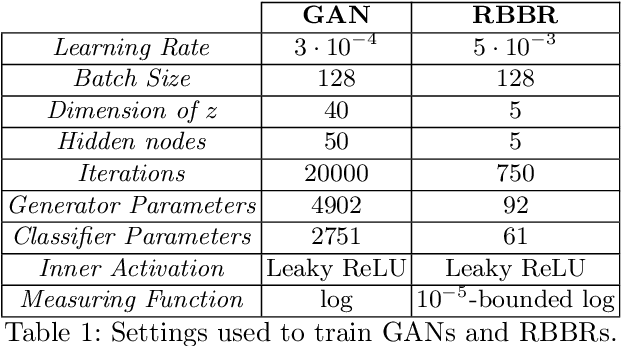
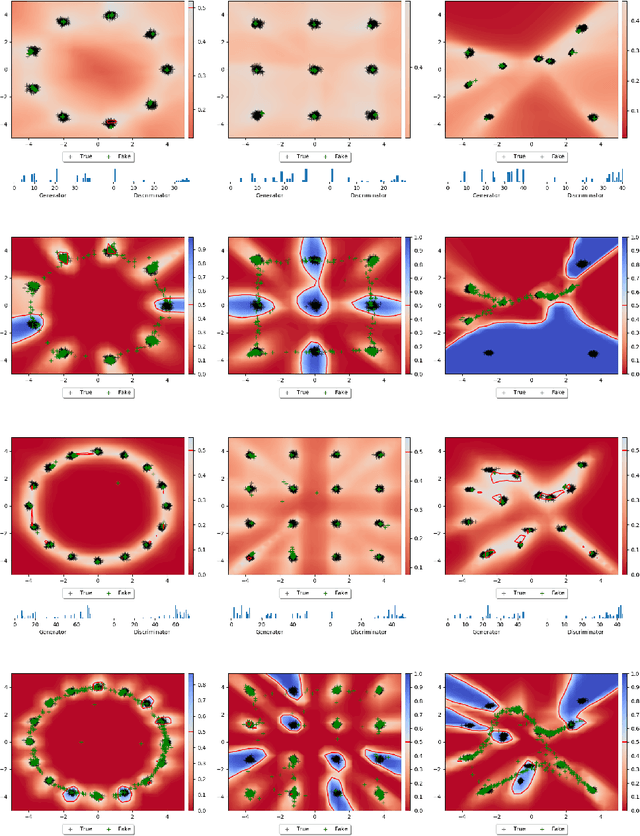
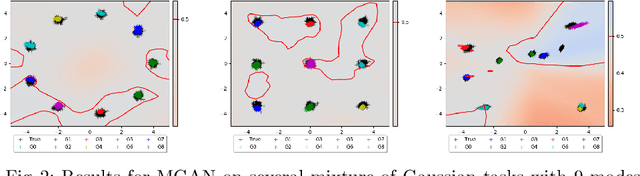
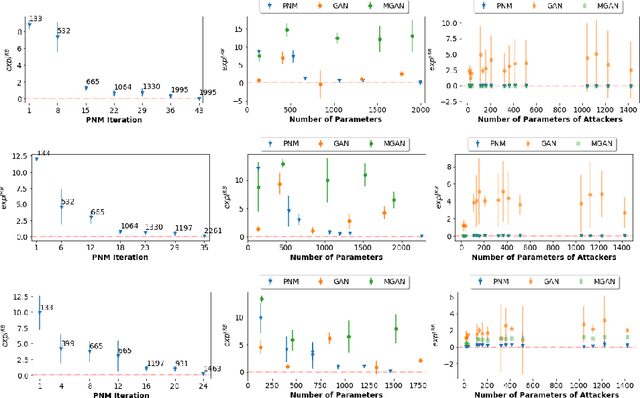
Save for some special cases, current training methods for Generative Adversarial Networks (GANs) are at best guaranteed to converge to a `local Nash equilibrium` (LNE). Such LNEs, however, can be arbitrarily far from an actual Nash equilibrium (NE), which implies that there are no guarantees on the quality of the found generator or classifier. This paper proposes to model GANs explicitly as finite games in mixed strategies, thereby ensuring that every LNE is an NE. With this formulation, we propose a solution method that is proven to monotonically converge to a resource-bounded Nash equilibrium (RB-NE): by increasing computational resources we can find better solutions. We empirically demonstrate that our method is less prone to typical GAN problems such as mode collapse, and produces solutions that are less exploitable than those produced by GANs and MGANs, and closely resemble theoretical predictions about NEs.